Depuis qu’elle a été introduite au monde occidental au XIIIe siècle, la suite de Fibonacci ne cesse de fasciner les mathématiciens, les artistes, et même les élèves ! Eh oui, la suite de Fibonacci est souvent choisie comme sujet de Grand oral (elle est famous 😎) !
Pourquoi ? Parce que cette fameuse suite est un symbole de l’harmonie parfaite et elle nous en apprend plus sur la nature qui nous entoure. Ça t’intrigue ? Ça te paraît flou ? Tu ignores ce qu’est l’harmonie parfaite ? Tu veux savoir pourquoi on associe toujours la suite de Fibonacci au nombre d’or ? Pas de panique ! On te dit tout dans cet article ! 👇
Quelle est l’histoire de la suite de Fibonacci ? 🤔
La suite de Fibonacci, c’est quoi ? 🧑🏫
Pour comprendre pourquoi les élèves de spé maths sont friands de ce sujet de Grand oral, il faut remonter (un peu 👀) dans le temps et définir les termes.
En 1202, le mathématicien italien Leonardo Fibonacci, connu sous le nom de « Leonardo Pisano », parle d’une suite de nombres qui répond à une logique bien particulière.
💡 Le savais-tu ?
Leonardo Fibonacci (vers 1170 – vers 1250) est célèbre pour son Liber abaci (1202), un traité sur les calculs et la comptabilité, dans lequel il introduit le système de numération indo-arabe en Europe (1, 2, 3, 4, 5, 6, 7, 8, 9 et 0) au détriment des chiffres romains.
Plus précisément, c’est une suite de nombres entiers dont les dix premiers termes sont 0, 1, 1, 2, 3, 5, 8, 13, 21 et 34. Et après ? Eh bien, la suite de Fibonacci est infinie ! Rassure-toi, il faut juste mémoriser sa règle de construction. Chaque terme (à l’exception des deux premiers) est la somme des deux termes précédents. C’est ce qu’on appelle une « suite récurrente » !
👉 0 + 1 = 1 ; 1 + 1 = 2 ; 1 + 2 = 3 ; 2 + 3 = 5 ; 3 + 5 = 8 ; 5 + 8 = 13 ; etc.
À lire aussi
🔺 Tout savoir sur le triangle isocèle !
L’exemple des couples de lapins 🐰
Dans Liber abaci, Leonardo Fibonacci donne l’exemple de couples de lapins. Au départ, tu as un couple de lapins, qui donne naissance à un couple de lapereaux un mois plus tard. Ce dernier, une fois arrivé à maturité un mois plus tard, donne à son tour naissance à un couple de lapereaux, et ainsi de suite… Pour t’aider à comprendre, on t’a fait un schéma récap’ ! 👇
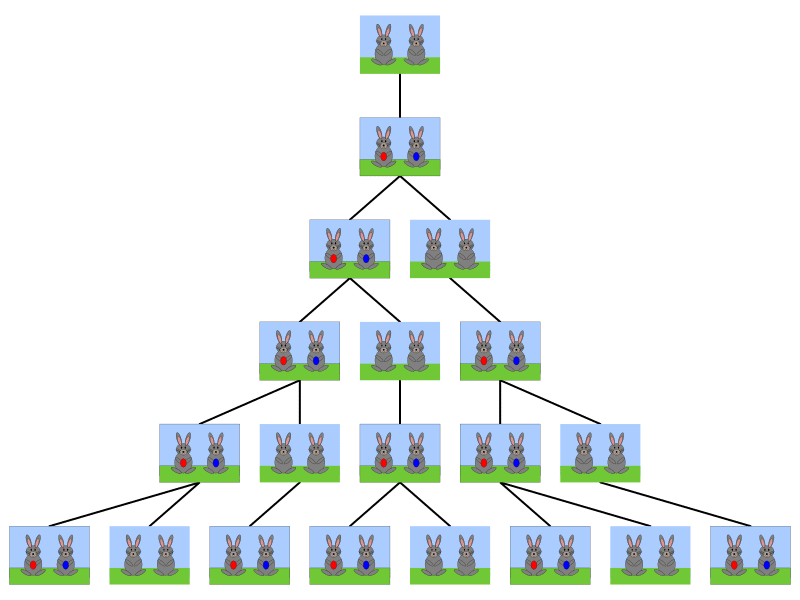
👉 Ici on voit que le total de lapins cumulés jusqu’à la génération de degré n serait le nombre Fn de Fibonacci. Si tu as fait attention, tu remarques que cet exemple de suite de nombres de couples de lapins correspond à la suite de Fibonacci : 0, 1, 1, 2, 3, 5, 8, 13, etc.
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Quel est le rapport entre le nombre d’or et la suite de Fibonacci ? 🧐
Le nombre d’or, c’est quoi ? 🔢
Et le nombre d’or dans tout ça ? Qu’est-ce que c’est exactement ? Pourquoi l’associe-t-on à la suite de Fibonacci ? Patience, on y arrive ! Commençons par définir les termes ! 😉
↪️ Selon Le Robert en ligne
Le nombre d’or désigne le « rapport entre la plus grande des deux parties et la plus petite, égal au rapport entre le tout et la plus grande » dans le partage asymétrique d’une peinture.
👉 À l’origine, on utilise donc le terme « nombre d’or » pour parler en géométrie de l’unique rapport entre deux longueurs telles que le rapport de la somme des deux longueurs (a+b) sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b). ll s’écrit :
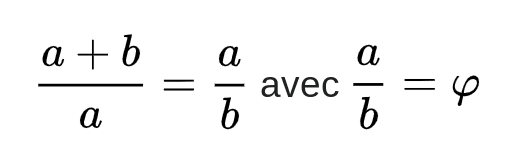
Le nombre d’or, souvent désigné par la lettre φ (phi) en l’honneur du sculpteur Phidias, donne aussi le nombre irrationnel phi. Sa valeur exacte est de (1+√5)/2, ce qui équivaudrait à :
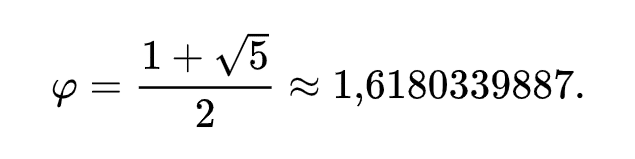
🚨 Rappel : un nombre « irrationnel » ne peut pas être mis sous la forme d’un rapport entre deux nombres entiers. Les exemples les plus connus sont π et e !
À lire aussi
🔢 Fiche de maths : les nombres premiers !
Le nombre d’or, un nombre de la suite de Fibonacci 🚶
Le rapport, le voilà : le nombre d’or provient de la suite de Fibonacci, qui a un taux de croissance exponentiel qui tend vers le nombre d’or. Ce rapport est considéré comme LA clé de l’harmonie universelle et se transpose par des formes géométriques.
↪️ Exemples
- Le rectangle ;
- Le pentagone ;
- Le triangle ;
- Le cercle.
👉 Plus on avance dans la suite de Fibonacci, plus l’écart entre le rapport de deux de ses termes successifs et le nombre d’or s’amenuise. Par exemple, 21/13 est égal à 1, 615384. Mais si on calcule 34/21, on voit que le rapport suivant s’en approche : 1, 619047. 💭
Ton premier cours particulier de maths est offert ! 🎁
Tous nos profs sont passés par les meilleures écoles de France !
Peut-on trouver le nombre d’or dans la nature ? 🍃
Maintenant, prépare-toi à être ébloui (mode sunglasses activé 😎) ! Parce que oui, on n’appelle pas le nombre d’or « ratio d’or », « section dorée » ou encore « divine proportion » pour rien.
👉 Depuis qu’il a été introduit, tout le monde s’intéresse au nombre d’or :
- les mathématiciens ;
- les architectes ;
- les peintres ;
- les astrologues ;
- et on en passe !
La suite de Fibonacci et le nombre d’or sont des principes mathématiques qui sont omniprésents dans la nature. Ils ont même un lien avec une simple coquille d’escargot ! 🐌
Tu as notamment affaire au nombre d’or quand tu observes des motifs en forme de spirales, qui s’organisent en réseaux qui se croisent. Et si tu comptais les spirales de ces réseaux, tu verrais qu’on obtient souvent deux nombres consécutifs de la suite de Fibonacci.
Si tu n’arrives pas à résoudre ton problème de maths et que cette matière et toi, ça fait deux, tu peux prendre des cours de soutien scolaire de mathématiques en ligne ! 🎓
Découvre d’autres articles mathématiques !
Quelques exemples concrets 👇
Le nombre de pétales des fleurs est souvent 3, 5, 8, 13, 21, 34 ou 55. Les boutons d’or ont 5 pétales et les marguerites ont 34 ou 55 pétales. Ces nombres ne sont pas le fruit du hasard, ils font tous partie de la suite de Fibonacci !
Si tu observes le cœur d’un tournesol, tu verras deux séries de courbes qui ne sont pas enroulées dans le même sens. En général, le nombre de spirales est soit 21 et 34, soit 34 et 55, soit 55 et 89, ou soit 89 et 144. Encore une fois, la suite de Fibonacci est présente !
Le sculpteur grec Phidias (il est de retour !) aurait utilisé le nombre d’or pour concevoir la statue de la déesse Athéna au Parthénon, sur l’Acropole d’Athènes. Dans un rectangle d’or, le rapport de la longueur à la largeur est égal au nombre d’or.
L’Homme de Vitruve, le célèbre dessin de Léonard de Vinci, représente aussi cette volonté de définir un homme idéal. Les proportions de cet homme aux bras écartés, qui s’inscrit à la fois dans un cercle et un carré, respecteraient le rapport du nombre d’or.
À lire aussi
📕 Lycée : comment travailler la physique et les mathématiques ?
Récapitulatif ✅
📍 La suite de Fibonacci a été introduite en Europe en 1202 par Leonardo Fibonacci.
📍 C’est une suite infinie de nombres entiers.
📍 Ses dix premiers termes sont : 0, 1, 1, 2, 3, 5, 8, 13, 21 et 34.
📍 C’est ce qu’on appelle une « suite récurrente ».
📍 L’exemple donné par Leonardo Fibonacci est celui de couples de lapins.
📍 Le nombre d’or est désigné par la lettre φ (phi) en l’honneur du sculpteur Phidias.
📍 Sa valeur équivaut à environ 1, 6180339887.
📍 Le nombre d’or provient de la suite de Fibonacci.
📍 Ce rapport est considéré comme la clé de l’harmonie universelle.
📍 Tu peux le transposer par des formes géométriques : triangle, rectangle, cercle…
📍 La suite de Fibonacci et le nombre d’or sont présents dans la nature.
📍 Exemples : dans les spirales d’une coquille d’escargot ou dans le nombre de pétales.
À lire aussi
🧮 6 podcasts de maths pour t’améliorer !
Conclusion
Tu l’auras compris, chaque être vivant est organisé selon des principes mathématiques tels que la suite de Fibonacci et le nombre d’or. Qu’il s’agisse des coquillages, des atomes ou encore des cristaux, de nombreux éléments naturels répondent à ces principes. Maintenant, tu sais pourquoi ils sont aussi étudiés en mathématiques ! 😜
PS : Le 23 novembre, c’est le Fibonacci Day ! Pourquoi ? Parce que la date sous sa forme mois-jour s’écrit 1 1 2 3 et ce sont les premiers termes de la suite de Fibonacci.
