Exemple des suites géométriques

Vous trouvez les suites géométriques complexes ? Un cours particulier de maths avec nos profs peut vous aider à démystifier leurs secrets. 🌀

Poursuivez votre apprentissage avec notre cours spécialisé sur les suites géométriques, conçu pour rendre leur maîtrise accessible et agréable !

Exemple des suites géométriques

Définition : suite géométrique

On appelle suite géométrique toute suite de la forme $\left( a q^n \right)_{n \in \mathbb{N}}$

avec $q \in \mathbb{R}$

et $a \in \mathbb{R}$

Proposition

Soit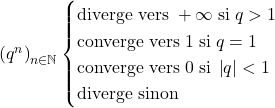 $q \in \mathbb{R}$

. La suite $\left( q^n \right)_{n \in \mathbb{N}} \begin{cases} \text{diverge vers}\; + \infty \; \text{si} \; q > 1 \\ \text{converge vers}\; 1 \; \text{si} \; q = 1 \\ \text{converge vers}\; 0 \; \text{si} \; \left| q \right| < 1 \\ \text{diverge sinon} \end{cases}$

Démonstration

Une simple étude de fonction permet de montrer que

$\forall x > -1, \; \forall n \in \mathbb{N}, \quad \left( 1 + x \right)^n \ge 1 + n x.$

Soit $q>1$

. Pour tout $n \in \mathbb{N}$

, on a $q^n = \left( 1 + q - 1 \right)^n \ge 1 + n \left( q - 1 \right) \xrightarrow[n \to + \infty]{}+ \infty$

. Par comparaison, on en déduit que $\left( q^n \right)_{n \in \mathbb{N}}$

diverge vers $+ \infty$

Si $q=1$

, la suite $\left( q^n \right)_{n \in \mathbb{N}}$

est constante égale à $1$

, donc converge et de limite égale à $1$

On suppose que $\left| q \right| < 1$

. Le cas où $q=0$

est clair car la suite $\left( q^n \right)_{n \in \mathbb{N}}$

stationne sur $0$

.
On suppose donc $q \neq 0$

. On a

$\forall n \in \mathbb{N}, \quad \left| q^n \right| = \left| q\right |^n = \mathrm{e}^{n \ln \left( \left| q \right| \right)} \xrightarrow[n \to + \infty]{} 0$

car $\ln \left( \left| q \right| \right) < 0$

et car $\lim\limits_{u \to - \infty} \mathrm{e}^{u} = 0$

Si $\left( q^n \right)_{n \in \mathbb{N}}$

converge vers une limite $\ell$

, alors $\left( q^{n+1} \right)_{n \in \mathbb{N}}$

converge vers $q \ell$

. Par unicité de la limite, $\ell$

vérifie $\ell = q \ell$

, soit $\ell = 0$

, ce qui est exclu car pour tout $n \in \mathbb{N}$

, $\left| q^n \right| \ge 1$

.
Un raisonnement analogue permet de montrer que la suite $\left( q^n \right)_{n \in \mathbb{N}}$

ne peut pas diverger vers $+ \infty$

ou $- \infty$

Exemple

La suite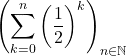 $\displaystyle{\left(\sum_{k=0}^n \left( \dfrac12 \right)^k \right)_{n \in \mathbb{N}}}$

converge vers $2$

car

$\forall n \in \mathbb{N}, \quad \sum_{k=0}^n \left( \dfrac12 \right)^k = \dfrac{1- 1/2^{n+1}}{1- 1/2} \underset{n \to + \infty}{\longrightarrow} 2.$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

Tu as aimé cet article ?

Sommaire

Exemple des suites géométriques

Sur le même sujet

Comment exploser tes épreuves de maths en prépa HEC ? 💥

Calcul pourcentage : fiche de maths

Loi de Poisson : fiche de maths 🔢

Ton premier cours est offert ! 🎁

4 points de plus sur ta moyenne en prenant des cours particuliers avec l’un de nos Sherpas ! 👇

William Mievre

Co-fondateur des Sherpas

Passé par une Prépa HEC puis l'ESCP, j'ai donné des centaines d'heures de cours particuliers avant de créer Les Sherpas avec Étienne. Passionné d'éducation, je te partage désormais mes meilleurs conseils afin de t'aider à réussir et t'épanouir dans tes études. Cheers ✌️💖 !

Prépa Prépa scientifique

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉

Annuler la réponse

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉