Tu as peut-être vu la loi de Poisson en cours, mais tu n’y comprends pas grand-chose ? Tu t’intéresses aux probas, mais tu n’as jamais entendu parler de cette loi ? Bouge pas ! On t’a préparé une fiche de maths pour t’aider à la connaitre, à la comprendre et même à l’utiliser. Tu es prêt ? C’est parti 🚀
La loi de Poisson, c’est quoi ? 👀
Histoire de la loi de Poisson 📖
D’où vient la loi de Poisson ? Pourquoi s’appelle-t-elle comme ça ? Eh bien, elle a tout simplement pris le nom de famille du mathématicien qui l’a théorisée. Rien à voir avec la pêche donc. 🐟 Siméon Denis Poisson a introduit la loi de Poisson en 1838 dans son ouvrage Recherches sur la probabilité des jugements en matière criminelle et en matière civile.
La vie n’est bonne qu’à deux choses : découvrir les mathématiques et enseigner les mathématiques.
Siméon Denis Poisson
mathématicien
💡 Le savais-tu ?
Siméon Denis Poisson a publié de nombreux travaux, près de 400 dans les domaines de mathématiques appliquées et la physique ! Sa publication sur la loi qui porte son nom n’a pas fait grand bruit à son époque, mais a eu une grande influence par la suite. La preuve, on en parle encore aujourd’hui !
Définition 🧐
Maintenant que tu sais d’où vient la loi de Poisson, on va t’expliquer ce qu’est cette loi et à quoi elle sert. Oui, c’est bien beau de la définir, mais si on ne sait pas quand l’utiliser, ça ne sert à rien.
Une variable aléatoire discrète qui suit une loi de Poisson de paramètre lambda est définie par la formule suivante :
Donc, à chaque fois que X va prendre la valeur k alors sa probabilité sera égale à :
est un nombre réel strictement positif
(c’est la base de la fonction exponentielle)
(factorielle de k)
On note que X suit une loi de Poisson de paramètre lambda :
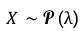
🧐 Discret VS continu
👉 Une loi de probabilité est discrète quand l’expérience aléatoire ne peut prendre qu’un nombre limité de valeurs.
👉 Une loi de probabilité est continue quand l’expérience aléatoire peut prendre n’importe quelle valeur dans un intervalle défini.
Mais concrètement, on l’utilise pour quoi ? En statistique, la loi de Poisson est la loi des évènements rares, des petites probas. Eh non, on ne parle pas de la proba que ton crush t’invite à boire un verre ce week-end. On l’utilise pour modéliser des expériences de comptage en remplissant quelques conditions :
✅ Il faut que ça soit très rare d’avoir 2 succès en même temps.
✅ Le nombre moyen de succès pendant un temps t ne dépend que de sa durée.
✅ L’arrivée d’un succès est indépendant du précédent.
Voici quelques exemples d’évènements où on peut utiliser la loi de Poisson pour calculer la probabilité qu’ils arrivent :
📍 Nombre de véhicules qui passent un poste de péage en période creuse, durant 1 heure.
📍 Nombre de personnes arrivant dans une file d’attente entre 15h et 15h30.
📍 Nombre de taxis passant à un endroit donné durant un intervalle de temps.
⚠️ Pas la même chose pour les bus et les trains !
Les bus et les trains passent à des horaires fixes. Le futur dépend donc du passé, car c’est fixé par l’heure de départ. 🚌
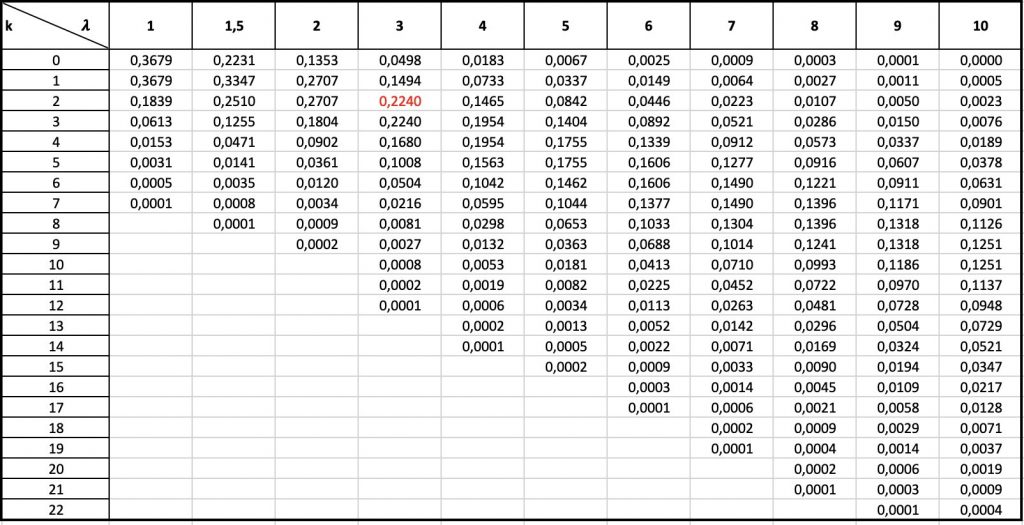
Pour trouver les approximations, tu peux utiliser la table de la loi de Poisson. Il te suffit juste de regarder le paramètre lambda et la valeur que tu cherches.
👉 Exemple
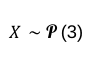
Quelle est la probabilité que X = 2 ?
Tu peux utiliser la formule :
Mais si tu ne veux pas trop de fouler, tu peux lire directement dans la table loi de Poisson et tu trouves 0,224. Comme par hasard !

💡 Le savais-tu ?
Tu peux créer ta propre table de la loi de Poisson sur excel !
Voici la formule :
=LOI.POISSON.N(x;espérance;cumulative)
x : tu entres la valeur que tu veux trouver (notre k)
espérance : c’est le lambda λ
cumulative : tu tapes 0
À lire aussi
✅ Découvre nos conseils pour progresser en maths en prépa !
Espérance et variance 🤓
Son espérance et sa variance sont les mêmes ! Ce sont les caractéristiques de cette loi. On va te le démontrer. Mais avant, on va revoir ce que sont l’espérance et la variance en mathématiques.
💡 Rappel
👉 L’espérance de X, notée E(X), est la moyenne des valeurs possibles de X pondérée par les probabilités que ces valeurs arrivent.
👉 La variance de X, notée V(X), est l’écart moyen entre chaque valeur et la moyenne. En gros, ça permet de voir si les différentes valeurs sont plus ou moins dispersées.
Plus la variance sera élevée, plus les valeurs seront dispersées par rapport à la moyenne.
Maintenant que tu as revu ce que sont l’espérance et la variance, on peut te démontrer qu’elles sont égales pour la loi de Poisson !
Pour la loi de Poisson, on va noter la formule de l’espérance comme ça :
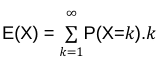
On calcule bien la moyenne des valeurs possibles de X (représentée par k) pondérée par la probabilité que ça soit k.
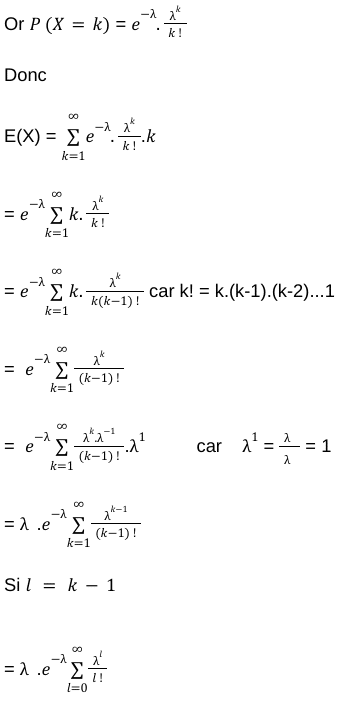
💡 Rappel sur la fonction exponentielle
Le développement en série entière de exp (x) :
est le développement de la série entière de
On a donc
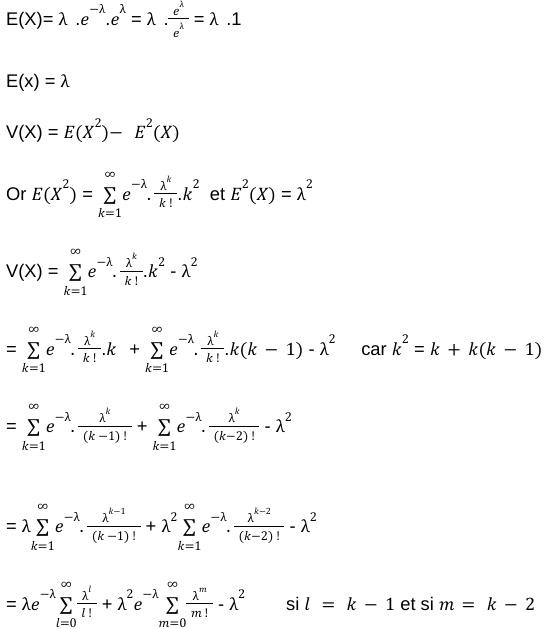
et
sont les développements de la série entière de
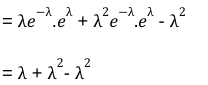
V(X) =
C’est fini 🥲 Donc, tout ça pour te montrer que l’espérance et la variance sont égales à lambda !


Ton premier cours particulier est offert ! 🎁
Nos profs sont passés par les meilleures écoles et universités.
Approximation de la loi binomiale par la loi de Poisson 🤔
Avant de faire l’approximation de la loi binomiale par la loi de Poisson, on va définir la loi binomiale. Oui, on sait que si tu es là, c’est que tu l’as déjà vue. Mais ça ne fait pas de mal, hein ?
La loi binomiale, de paramètres n et p, est la loi de probabilité d’une variable aléatoire X égale au nombre de succès rencontrés au cours d’une répétition de n épreuves de Bernoulli, p étant la probabilité de succès dans chacune d’entre elles.
On note :
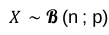
💡 Rappel sur Bernoulli
Soit une épreuve de Bernoulli de paramètre p et X une variable aléatoire discrète qui vaut 1 si l’épreuve donne un succès et 0 si elle donne un échec.
P(X= 1) = p et P(X=0) = 1- p, avec 0 ≤ p ≤ 1
Donc la loi binomiale est une loi de Bernoulli, mais avec plusieurs épreuves qui ne dépendent pas les unes des autres.
Contrairement à la loi de Poisson qui a un paramètre lambda, les lois de Bernoulli et Binomiale ont deux paramètres.
Mais du coup, quel rapport entre la loi binomiale et celle de Poisson ? Eh bien, sous certaines conditions, une loi binomiale se rapproche d’une loi de Poisson. Les voici 👇
✅ n ≥ 30 : le nombre d’expériences assez grand
✅ p ≤ 0,1 : la proba d’avoir un succès assez petite
✅ np < 15 : l’espérance d’avoir un succès assez petite
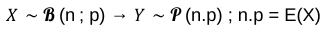
Mais pourquoi ? Quand on y pense, ça paraît assez logique. Si les épreuves sont nombreuses et indépendantes, et qu’il y a peu de probabilités pour avoir un succès, c’est que c’est un phénomène rare ! Donc, on peut utiliser la loi de Poisson !

Approximation de la loi de Poisson par la loi normale 🤨
On a vu qu’on peut rapprocher une loi Binomiale par une loi de Poisson. Maintenant, on va voir sous quelles conditions une loi de Poisson s’approxime par une loi normale.
💡 Rappel sur la loi normale
La loi normale est une représentation de données selon laquelle la plupart des valeurs sont regroupées autour de la moyenne et les autres s’en écartent symétriquement des deux côtés.
👉Exemple
La taille des humains suit une loi Normale. La plupart des personnes sont de taille moyenne. Mais plus elles sont grandes ou petites, moins elles seront nombreuses.
Une loi de Poisson s’approxime par une loi Normale quand λ > 18
Mais pourquoi ? Tout simplement parce que la table de la loi de Poisson s’arrête à λ = 18. Eh oui, il fallait bien l’arrêter à un moment. Dans la table, tu peux voir que plus lambda est grand, plus la probabilité d’avoir un évènement diminue. D’où cette approximation par la loi Normale.
Du coup, si λ > 18 :
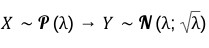
À lire aussi
✅ Découvre notre fiche de cours sur les suites arithmétique et géométrique !


Besoin d’un prof particulier ? ✨
Nos profs sont là pour t’aider à progresser !
Exercices 📝
On espère que tu as bien compris la théorie. Maintenant place à la pratique !

Exercice 1
Dans un parking, le nombre moyen d’arrivées de véhicules est de 120 par heure.
Calcule la probabilité pour qu’il y ait 3 véhicules qui arrivent durant 4 minutes.
Exercice 2
Dans une entreprise, il y a X accidents de travail par an. X est une variable aléatoire discrète qui suit une loi de Poisson de paramètre 2.
- Calcule la probabilité qu’il n’y ait aucun accident pendant l’année.
- Calcule la probabilité qu’il y ait au moins 3 accidents pendant l’année.
- Calcule la probabilité qu’il y ait moins de 3 accidents pendant l’année.
Corrections ✅
Correction exercice 1
Soit X, la variable aléatoire discrète qui représente le nombre de véhicules qui passent le péage dans un intervalle de temps t.

Il te faut déterminer le paramètre lambda :
🤔 Pourquoi λ = 8 et non 120 ?
On a la moyenne sur une heure qui est de 120. Or, on veut calculer la probabilité sur 4 minutes. Tu dois prendre en compte l’intervalle de temps. Sinon c’est comme si tu calculais la probabilité d’avoir 3 véhicules dans l’heure.
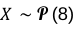
Le calcul :
💡 Idée
Va directement dans la table de la loi de Poisson !
La probabilité que 3 véhicules entrent dans le parking en 4 minutes est de 2,86 %
Correction exercice 2
Tu sais déjà, d’après l’énoncé, que X suit une loi de Poisson de paramètre lambda = 2
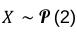
1. Calcul de la proba qu’il n’y ait aucun accident pendant l’année :
👉 On a 13,53 % de chance qu’il n’y ait aucun accident pendant l’année.
2. Calcul de la proba qu’il y ait au moins 3 accidents pendant l’année :
👉 On a 32,33 % de chance qu’il y ait au moins 3 accidents pendant l’année.
3. Calcul de la proba qu’il y ait moins de 3 accidents pendant l’année :
👉 On a 67,67 % de chance qu’il y ait moins de 3 accidents pendant l’année.



Besoin de cours particuliers ? ✨
4 points de plus sur ta moyenne avec nos profs Sherpas ! 📈
Quiz❓
On te donne une situation et tu nous dis si on peut utiliser la loi de Poisson !
Et voilà, tu sais tout de la loi de Poisson ! 🤓 On espère que cette fiche de cours t’a bien aidé. Dis nous en commentaire si tu veux en savoir plus sur d’autres lois de probabilité ou sur un chapitre en mathématiques.


















Bonjour
Juste vous remercier