Durant ta scolarité, tu as appris chaque année une notion sur le triangle isocèle. Aujourd’hui, on te propose un récapitulatif de toutes ces informations en un seul et même endroit et ça commence maintenant ! 😋
Un triangle est une forme géométrique. Il est reconnaissable grâce à ses trois côtés. Il existe des dizaines de triangles aux caractéristiques différentes. Néanmoins, on appelle triangle isocèle un triangle qui possède deux côtés égaux (mais pas n’importe lesquels).
Un triangle ABC, dont le sommet est A, est isocèle si les côtés adjacents au point A sont égaux, soit AB=AC. Ainsi BC représente la base du triangle.
💡 Étymologie
Le mot isocèle vient du grec iso (mêmes) et skelos (jambes). Autrement dit, isocèle signifie quelque chose qui a les mêmes jambes. Or, le dessin d’un triangle isocèle fait penser aux deux jambes d’un dessin de bonhomme. Ainsi, le terme isocèle représente deux segments de même longueur.
À lire aussi
Les affirmations de base et leurs démonstrations
📍 Propriété générale
Un triangle isocèle possède deux côtés et deux angles égaux ; en ce sens, un axe de symétrie. Cet axe est la médiane de la base et la bissectrice de l’angle principal.
Démonstration :
Voici un triangle isocèle.
AB = AC. BC est la base du triangle.
La médiane (d) part de l’angle primordial et coupe la base BC perpendiculairement.
(d) est aussi la bissectrice qui sépare l’angle A en deux parts égales.
On justifie des segments de même longueur par // ou /.
📍 Propriété 1
Un triangle isocèle possède deux côtés identiques et deux angles de même mesure à la base. ⇾ Si un triangle possède deux angles identiques, alors il est isocèle !
Démonstration :
Si AB et AC sont égaux,
Alors l’angle B et l’angle C sont identiques.
Donc ABC est un triangle isocèle.
📍 Propriété 2
Dans un triangle ABC isocèle en A, la médiane, la hauteur et la bissectrice sont toutes issues de A ainsi que la médiatrice de la base BC. Elles sont donc confondues.
Dans un triangle isocèle, ces trois segments sont confondus, c’est-à-dire, qu’ils sont tous les mêmes, passant par le même sommet et la base.
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Les formules de calcul 📏
Calculer la hauteur 🪜
Pour calculer la hauteur h, on utilise le théorème de Pythagore qui donne la formule :
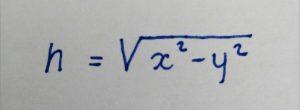
Démonstration :
Exemple :
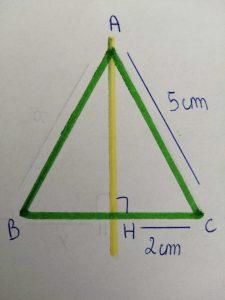
On a un triangle BAC dont h est perpendiculaire à BC en un point H. AC = 5 cm et HC = 2 cm.
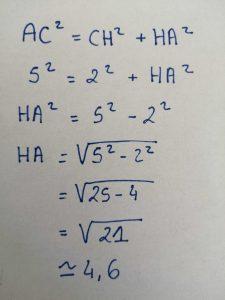
Calculer l’aire d’un triangle isocèle ▲
Pour calculer la surface, il suffit de prendre la formule du calcul de l’aire d’un triangle. Peu importe les attributs de la forme géométrique, la formule reste la même, à savoir :
A = base x h ÷ 2
Démonstration :
Le triangle BAC est isocèle en A. BC = 5 cm et AH
= 5,5 cm.
A = base x h ÷ 2
A = 5 × 5,5 ÷ 2
A = 13,75
La surface de A est de 13,75 cm².
À lire aussi
On dit souvent que le savoir, c’est le pouvoir. Plus tes connaissances seront nombreuses, plus il sera facile pour toi d’avancer dans ta scolarité. Si tu fais partie de ses élèves qui veulent toujours en savoir plus, n’hésite pas à te tourner vers un de nos professeurs particuliers de mathématiques ! 🧑🏫
Calculer le périmètre d’un triangle isocèle ꕔ
En ce qui concerne sa circonférence, c’est pareil. C’est la même formule pour tous les triangles.
P = c × c × c
ou
P = c × 3
Étant donné qu’il s’agit ici d’un triangle isocèle, deux côtés ont la même longueur x et la longueur de la base y. Tu peux donc aussi rencontrer la formule :
P = 2x + y
Démonstration :
Ici, on a un triangle BAC isocèle en A. Puisqu’il est isocèle, AC = AB = 5 cm.
Sa base BC est coupée en son centre par la médiane. Autrement dit, HC + HB = 2 + 2 = 4 cm. Donc BC = 4 cm.
On utilise la formule : P = 2x + y
P = 2 × 5 + 4
P = 10 + 4
P = 14
Donc le périmètre est de 14 centimètres.
À lire aussi
Collégien en galère ? Ton premier cours est offert ! 🎁
Nos profs sont là pour t’aider à progresser !
Les cas particuliers 🤓
Les triangles rectangles isocèles ◺
Le triangle rectangle isocèle est représenté avec les mêmes caractères que les triangles isocèles étudiés jusqu’à présent. La seule différence concerne l’angle primordial.
Prenons le cas de la figure MNO.
Par définition, un triangle est rectangle lorsqu’un de ces angles équivaut à 90°, soit un angle droit. Ici, MNO est rectangle en N.
Il est également isocèle, car deux de ses côtés ont des mesures identiques, MN = NO.
💡 Comment calculer l’aire d’un triangle rectangle isocèle ?
Exactement de la même manière que pour tous les types de formes triangulaires : base x h ÷ 2
Exemple :
Un triangle MNO est rectangle en O et isocèle car MO = NO. MO = 6 cm ; MN = 8 cm et h = 4 cm.
Pour calculer l’aire :
A = base x h ÷ 2
A = 8 × 4 ÷ 2
A = 32 ÷ 2
A = 16
La surface est de 16 cm².
Les triangles équilatéraux △
Pour ce cas, les trois côtés de la forme géométrique ont les mêmes longueurs. En ce sens, le triangle est forcément isocèle en chacun de ses angles.
Peu importe la longueur des côtés, un triangle équilatéral aura toujours ces angles à 60°.
Prenons le cas de la figure MNO.
Par définition, un triangle équilatéral possède ses trois côtés et ses trois angles égaux.
Donc MN = NO = OM et tous les angles mesurent 60°.
Tu veux cartonner au brevet ? ✨
Nos profs sont là pour t’aider à progresser !
Voici quelques exercices pour t’entraîner 🖩
- Voici XYZ, définit sa forme avec l’affirmation adaptée.
2. Calcule h toujours avec XYZ.
3. Trouve l’aire de XYZ avec les résultats obtenus.
Corrections des exercices !
- Dans ce cas, on peut identifier la propriété 1.
Un triangle isocèle possède deux côtés égaux et deux angles de même mesure à la base. ⇾ Si un triangle possède deux angles identiques, alors il est isocèle !
- On utilise le théorème de Pythagore.
Le résultat obtenu doit être d’environ 5,4 cm.
- On utilise la formule : A = base x h ÷ 2.
La surface est de 13,5 cm².
Nul en maths ? Essaye le retro-engineering !
Tu sais à présent tout au sujet du triangle isocèle ! Plus aucune excuse pour résoudre des problèmes en cours de géométrie et le contrôle, c’est les doigts dans le nez. Si cette fiche de cours t’a bien aidé, n’hésite pas à l’envoyer à tes amis pour comparer vos résultats et à nous dire en commentaire dans quelles autres matières tu as des difficultés. 😎
