En mathématiques, parmi les différentes fonctions, il existe les fonctions affines. D’ailleurs, au programme de 3e au collège, on te demande de bien les connaître et de savoir les déterminer dans des exercices. Mais alors, comment déterminer une fonction affine ? Ça tombe bien, c’est justement le sujet de cette petite fiche de cours !
Pour commencer : un peu de vocabulaire
Tu as normalement appris qu’une fonction f est un procédé mathématique associant à chaque nombre x un unique nombre y. On note f(x) = y (ce qui se lit « f de x égal y »).

x s’appelle la variable et les valeurs prisent par x s’appellent les antécédents.
👉 y est le résultat de la transformation d’un antécédent x par la fonction f : il s’appelle l’image de x par la fonction f et se note f(x). On écrit alors que : y = f(x).
À lire aussi
Comment bien réviser les maths pour un examen ? 👌
Définition de la fonction affine
Une fonction affine est une fonction représentée par une droite (elle est linéaire). Sa particularité par rapport aux autres fonctions est que son taux d’accroissement est constant.
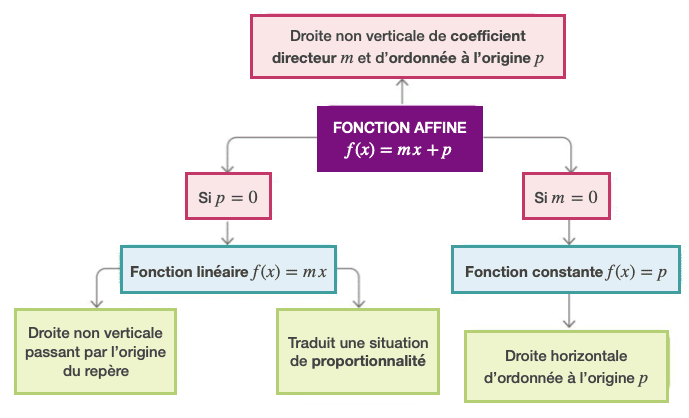
- m et p sont deux nombres donnés. La fonction f qui associe à tout nombre x le nombre mx + p est une fonction affine. Son expression algébrique s’écrit : f(x) = mx + p.
- m est le coefficient directeur de la fonction et on ajoute p au résultat.
- Par une fonction affine, chaque image a un seul antécédent.
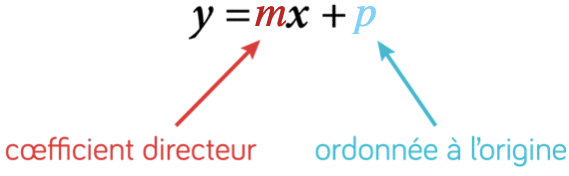
👉 La représentation graphique d’une fonction affine est une droite.
- Les antécédents d’une valeur se lisent sur l’axe des abscisses
- L’image d’une valeur se lit sur l’axe des ordonnées
Exemple : La représentation graphique de : f(x) = 3x + 2 est :
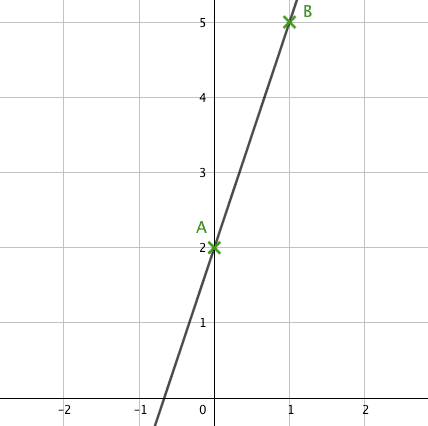
On a bien l’image de 0 qui est 2, soit le point A(0 ; 2) et celle de 1 qui est 5, donc le point B(1 ; 5).
Psst ! Les fonctions affines ne doivent pas être un obstacle insurmontable : renforce tes compétences et gagne en confiance avec l’aide d’un prof particulier de maths à domicile passionné et pédagogue ! ✨
Comment représenter une fonction affine ?
À l’aide de deux points
Traçons la courbe représentative de la fonction affine f(x) = 2x + 1 dans un repère.
Méthode :
- La représentation graphique d’une fonction affine est une droite.
- Donc on détermine deux points de la droite pour pouvoir la tracer.
- Pour cela, on choisit deux nombres quelconques et on calcule leur image.
Solution :
Une fonction affine est représentée par une droite.
On choisit deux nombres quelconques, par exemple –2 et 3. Puis on calcule leur image :
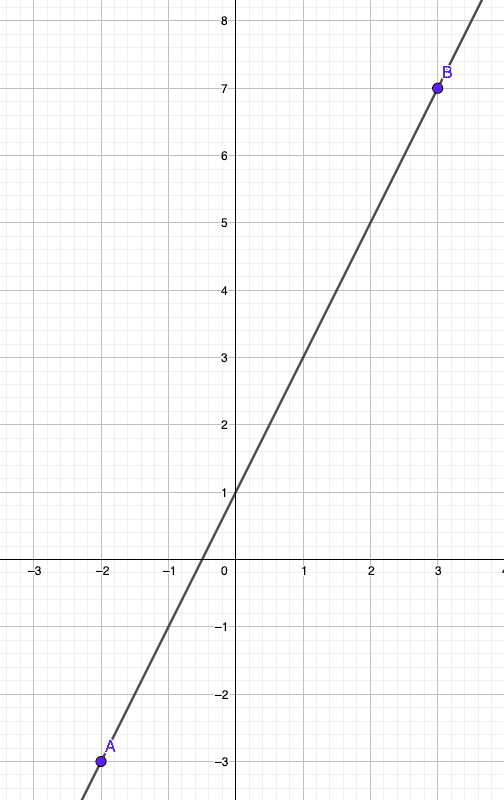
- f(–2) =2(–2) + 1 = –4 + 1 = –3 donc la droite passe par le point A(–2 ; -3).
- f(3) = 23 + 1 = 6 + 1 = 7 donc la droite passe par le point B(3 ; 7).
La droite (AB) est donc la courbe représentative f.
NB : Choisis des valeurs de x dont la différence est significative afin d’obtenir des points espacés.
À lire aussi
Pour progresser en maths, essaie notre méthode du reverse engineering ! 👍
Avec le coefficient directeur et de l’ordonnée à l’origine
Traçons dans un repère la courbe représentative de la fonction affine f de paramètre m = –2 et p = 4.
Méthode :
- On place le point A(0 ; p)
- À partir du point A, on place le point suivant à l’aide du coefficient directeur
- Pour cela, on avance d’une unité sur l’axe des abscisses et on monte de p sur l’axe des ordonnées si p est positif ou on descend de p si p est négatif.
Solution :
Une fonction affine est représentée par une droite.
m est le coefficient directeur de la droite et p est l’ordonnée à l’origine de la droite.
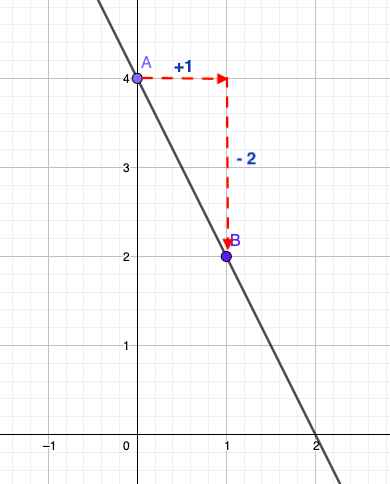
Ici, p = 4, la droite passe donc par le point A(0 ; 4).
Ici, m = –2 , or –2 < 0 donc on descend de 2 sur l’axe des ordonnées quand on avance de 1 sur l’axe des abscisses. La droite passe donc par le point A(1 ; 2)



Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Comment déterminer une fonction affine ?
À partir de deux points sur un graphisme
Prenons le graphique ci-dessous comme exemple.
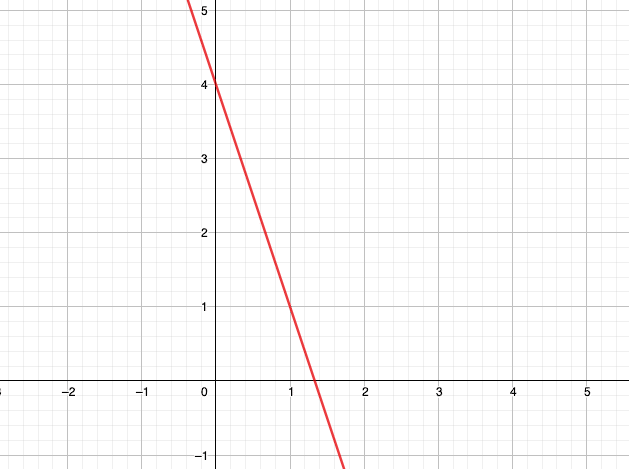
💡 Méthode
- Pour déterminer l’ordonnée à l’origine : on regarde la valeur au point d’intersection entre l’axe des ordonnées et la droite
- On détermine le signe du coefficient directeur : si f est croissante alors m > 0 et si f est décroissante alors m < 0
- Pour déterminer la valeur du coefficient directeur : on part d’un point sur la droite et on avance d’une unité sur l’axe des abscisses, puis on regarde de combien il faut monter ou descendre sur l’axe des ordonnées pour rejoindre la droite.
Solution :
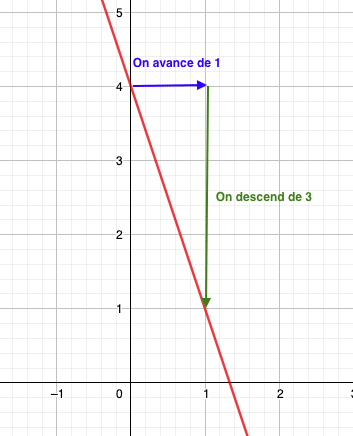
On regarde la valeur du point d’intersection entre la droite et l’axe des ordonnées :
f(0) = 4 = p
La droite est décroissante, donc on sait que m < 0
Quand on augmente x de 1, on constate que pour rejoindre la courbe, on descend de 3, donc : m = – 3
On en déduit que l’expression de f est : f(x) = –3x + 4

Les maths, quelle galère ! Tu veux guérir ta phobie de la matière ? Regarde cette vidéo 👇
Déterminer l’expression d’une fonction affine à partir d’un calcul
Prenons la fonction f ci-dessous dont la droite passe par les points A(2 ; 2) et B(6 ; 3).
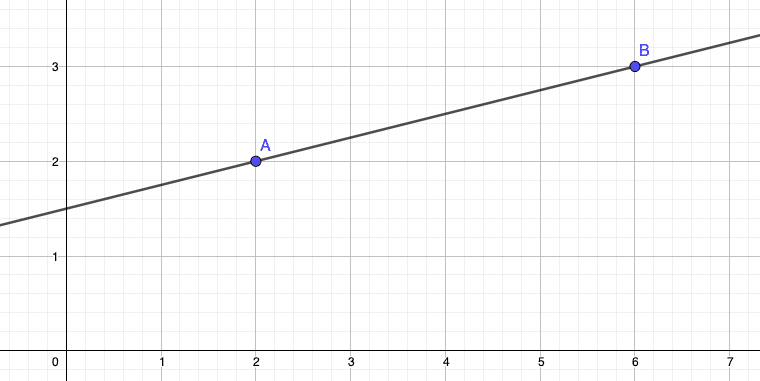
Méthode :

Solution :
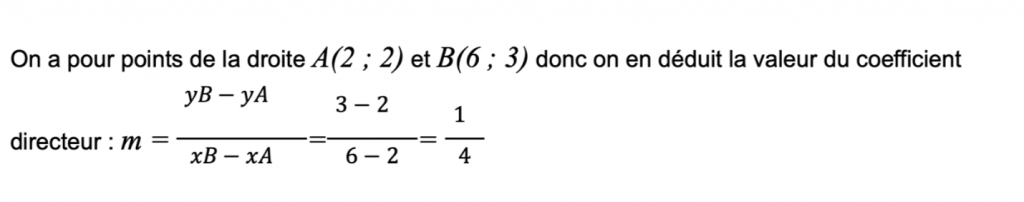
On détermine maintenant la valeur de l’ordonnée à l’origine, on a :
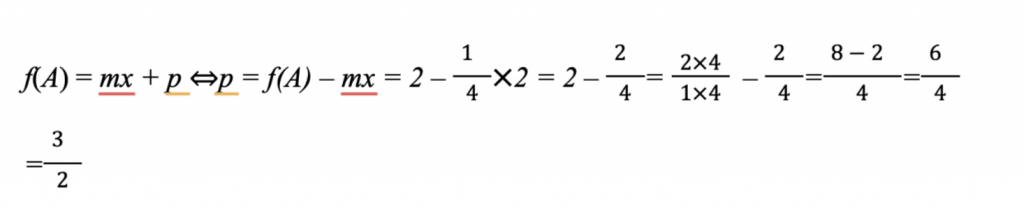
On peut donc en déduire l’expression de f 👇
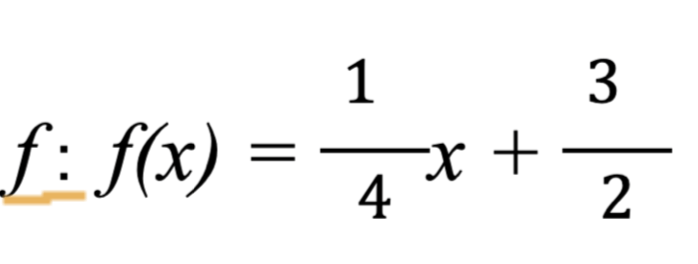


Tu veux cartonner au brevet ? ✨
Nos profs sont là pour t’aider à progresser !
Cas particulier de la fonction affine : la fonction linéaire
Définition de la fonction linéaire
- Une fonction linéaire est un cas particulier de la fonction affine.
- Pour un nombre m, la fonction f qui associe à tout nombre x le nombre mx est une fonction linéaire. Son expression algébrique s’écrit : f(x) = mx
- Elle se caractérise par une droite passant par l’origine du repère
- Elle représente une situation de proportionnalité avec comme coefficient de proportionnalité le coefficient directeur de la fonction linéaire, m.
- Par une fonction linéaire, chaque image a un seul antécédent.
Exemple : La représentation graphique de f(x) = 3x est :
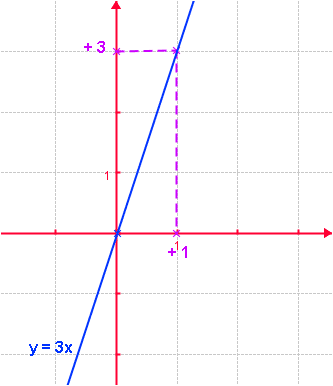
👉 On a bien l’image de 1 qui est 3, soit le point (1 ; 3)
Déterminer le coefficient d’une fonction linéaire
On considère la fonction linéaire f telle que f(4) = 2. Déterminons son coefficient directeur m.
Méthode :
- f est une fonction linéaire donc f(x) = mx
- On peut donc exprimer f(3) en fonction de m grâce à son expression algébrique
- Or on connaît la valeur de f(3) donc on peut résoudre une équation d’inconnu m.
Solution :
La fonction f est linéaire donc f(4) = 2 peut s’écrire sous la forme f(x) = mx
Donc on peut remplacer les x dans l’expression algébrique par 4, donc on a :
f(4) = m*4 or f(4) = 2 donc m*4 = 2
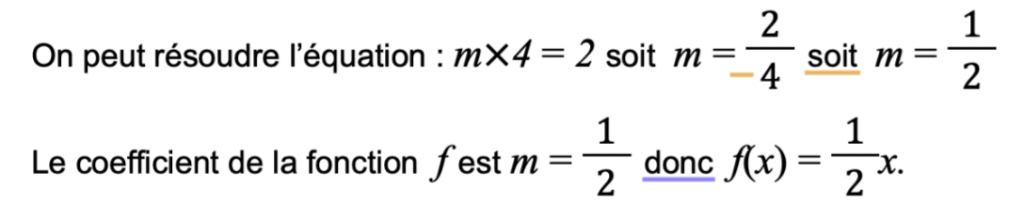

Représenter une fonction linéaire 🔍
Représentons dans un repère la fonction linéaire f telle que f(x) = 2x.
Méthode :
- Une fonction linéaire se caractérise par une droite passant par l’origine du repère.
- Donc on considère l’origine du repère comme un premier point, et il suffit de trouver un second point de cette droite pour pouvoir la tracer.
- Pour cela, on choisit un nombre quelconque et on calcule son image.
Solution :
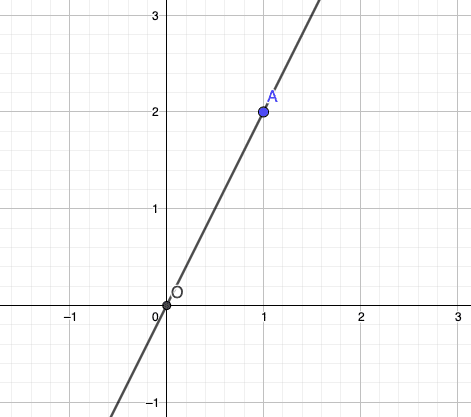
Une fonction linéaire est représentée par une droite passant par l’origine O du repère. On choisit un nombre quelconque, par exemple 1 et on calcule son image :
f(1) = 21 = 2 donc la droite passe aussi par le point A(1 ; 2).
La droite (OA) est donc la courbe représentative f.
Tips 💡
Selon l’échelle de ton graphique, tu peux choisir des points plutôt éloignés pour plus de précision. Tu peux aussi placer un troisième point pour vérifier l’alignement.
À lire aussi
Découvre le programme de maths en Seconde pour prendre de l’avance 🔍
Synthèse sur les fonctions affines 💭
Pour conclure cet article, voilà un petit rappel sur les fonctions. Car souviens-toi bien que pour déterminer une fonction affine, il faut d’abord bien connaître son sujet ! 😉 Et si après tout ça le concept de fonction affine te semble flou, un cours particulier de maths en visio avec nos Sherpas s’impose ! 🧐