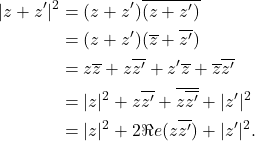Module d'un nombre complexe

Sommaire

Le corps des nombres complexes
Écriture algébrique d’un nombre complexe

Dans cet article, on présente une partie de la théorie sur les nombres complexes. C’est un outil très puissant que l’on retrouve aussi bien en géométrie, en analyse, en algèbre ou même en sciences physiques.

Pour approfondir votre compréhension des nombres complexes, y compris le complexe conjugué et le module, nos cours particuliers de maths, qui aborde l’algèbre et bien d’autres sujets, est une ressource inestimable. 📐

Le corps des nombres complexes

Quelques prérequis pour comprendre les nombres complexes

Rappel

On appelle produit cartésien de deux ensembles A et B l’ensemble, noté A x B, des couples (a,b) où a ∈ A et b ∈ B.

Définition de la Loi de composition interne

Soit $E$

un ensemble. On appelle loi de composition interne une application de $E\times E$

dans $E$

: $\varphi$

: $E\times E$

$\rightarrow$

$E$

( $x,$

y) $\mapsto$

$x \star$

Construction du corps des complexes

Définition

Nous appellerons corps des nombres complexes, noté $\mathbf{C}$

, l’ensemble $\mathbf{R}^2$

muni de deux lois internes $\oplus$

et $\otimes$

, définies pour tout $(a,b)\in\mathbf{R}^2$

, $(a',b')\in\mathbf{R}^2$

par :

$(a,b)\oplus (a',b')= (a+a',b+b'),$

$(a,b)\otimes (a',b')= (aa'-bb',ab'+a'b) .$

Remarques

En vue de simplifier les écritures, dans la suite, nous noterons $+$

et $\times$

(notations habituelles) les lois de composition interne $\oplus$

et $\otimes$

. La notion de corps sera vue ultérieurement.

Pour tout nombre réel a, nous identifions le nombre complexe (a,0) avec le réel a, et i le nombre complexe (0, 1). En utilisant cette notation et la définition de l’addition et de la multiplication dans C définies ci-dessus, on peut écrire pour tout nombre complexe (a,b) : (a,b) = a + ib.

Le signe égal ici est un abus de notation. Dans la suite, nous noterons un nombre complexe a + ib, c’est ce que l’on appelle la notation algébrique d’un nombre complexe. Avec cette notation, on notera classiquement ⊕ avec le signe + et ⊗ avec x.

Proposition

Le nombre complexe i vérifie i² = -1.

Démonstration

On a :

$\i^2=(0,1)\otimes (0,1)=(0\times 0-1\times 1, 0\times 1+1\times 0)=(-1,0)=-1.$

Écriture algébrique d’un nombre complexe

Partie réelle, partie imaginaire

Définition

Soit $z=a+\i b$

un nombre complexe.

$a$

est appelé partie réelle de $z$

, que l’on notera $\Re e(z)$

$b$

est appelé partie imaginaire de $z$

, que l’on notera $\Im(z)$

. On notera que la partie imaginaire est un nombre réel.

L’expression $z = a + \i b$

est appelée la forme algébrique du nombre complexe $z$

Remarque

Deux complexes seront égaux si, et seulement si, ils ont les mêmes parties réelles et les mêmes parties imaginaires.

Proposition

Un nombre complexe est réel si, et seulement si, sa partie imaginaire est nulle :

$z\in \mathbf{R}\Longleftrightarrow \Im(z)=0.$

Si un nombre complexe a une partie réelle nulle, on dit qu’il est imaginaire pur. On notera $\i\R$

l’ensemble des nombres imaginaires purs :

$z\in\i\mathbf{R}\Longleftrightarrow \Re(z)=0.$

Démonstration

Conséquence directe de la définition d’un nombre complexe.

Proposition : Linéarité des parties réelle et imaginaire

Soient $z$

et $z'$

deux complexes quelconques et $\lambda\in\R$

. Alors :

$\Re e(z+z')=\Re e(z)+\Re e(z')$

$\Re e(\lambda z)=\lambda \Re e(z)$

$\Im m(z+z')=\Im m(z)+\Im(z')$

$\Im m(\lambda z)=\lambda \Im m(z)$

Démonstration

On pose $z=a+\i b$

et $z'=a'+\i b'$

, alors : $z+z'=a+\i b+a'+\i b'=a+a'+\i(b+b')$

, ce qui prouve les points de la première ligne. Le reste se fait de la même manière.

Conjugué et module d’un nombre complexe

Définition

Soit $z=a+\i b$

un nombre complexe où $(a,b)\in\mathbf{R}^2$

On appelle complexe conjugué de $z$

que l’on note $\overline{z}$

le nombre complexe défini par :

$\overline{z}=a-\i b.$

On appelle module de $z$

que l’on note $|z|$

le nombre réel positif défini par :

$|z|=\sqrt{a^2+ b^2}.$

Proposition

Pour tout nombre complexe $z$

, on a :

$\Re e(z)=\dfrac{z+\overline{z}}{2}$

$\Im m(z)=\dfrac{z-\overline{z}}{2\i}$

$\overline{\overline{z}}=z$

$|z|^2=z\overline{z}$

Démonstration

Ces résultats s’obtiennent directement à partir des expressions algébriques.

Remarque

Le dernier point de la proposition précédente permet de vérifier que l’inverse d’un nombre complexe est encore un nombre complexe.

En effet, pour tout $z\in\mathbf{C}^*$

$\dfrac{1}{z}=\dfrac{\overline{z}}{|z|^2}.$

Exemple

Pour mettre sous forme algébrique le complexe $\dfrac{3+\i}{1-\i}$

, on multiplie le numérateur et le dénominateur par le conjugué du dénominateur :

$\dfrac{3+\i}{1-\i}=\dfrac{(3+\i)(1+\i)}{(1-\i)(1+\i)}=\dfrac{2+4\i}{2}=1+2\i.$

Proposition

Pour tout nombre complexe $z$

, on a :

$z=\overline{z}\Longleftrightarrow z\in\mathbf{R}$

$z=-\overline{z}\Longleftrightarrow z\in\i\mathbf{R}$

Démonstration

Soit $z=\Re e(z)+\i \Im m(z)$

un complexe.

$z=\overline{z}\Longleftrightarrow \Re e(z)+\i \Im m(z)=\Re e(z)-\i \Im m(z)\Longleftrightarrow \Im m(z)=-\Im m(z) \Longleftrightarrow \Im m(z)=0 \Longleftrightarrow z\in\mathbf{R}$$

$z=-\overline{z}\Longleftrightarrow \Re e(z)+\i b=-\Re e(z)+\i \Im m(z)\Longleftrightarrow \Re e(z)=-\Re e(z) \Longleftrightarrow \Re e(z)=0 \Longleftrightarrow z\in\i\mathbf{R}$$

Proposition

Pour tous nombres complexes $z$

et $z'$

, on a :

$\overline{z+z'}=\overline{z}+\overline{z'}$

$\overline{zz'}=\overline{z}\overline{z'}$

$\overline{\left(\dfrac{z}{z'}\right)}=\dfrac{\overline{z}}{\overline{z'}}$

, $z'\neq 0$

Démonstration

Ces résultats s’obtiennent directement à partir des expressions algébriques.

Proposition

Pour tout nombre complexe $z$

, on a :

$|z|=0\Longleftrightarrow z=0$

$|z|=|\overline{z}|$

$\Re e(z)\le |\Re e(z)|\le |z|$

$\Im m(z)\le |\Im m(z)|\le |z|$

Démonstration

Soit $z\in\mathbf{C}$

On pose $z=a+\i b$

, alors $|z|=0\Longleftrightarrow a^2+b^2=0\Longleftrightarrow a=0\text{ et } b=0\Longleftrightarrow z=0$

On a $|z|^2=z\overline{z}=|\overline{z}|^2$

On remarque que $\Re e(z)^2\le \Re e(z)^2+\Im m(z)^2=|z|^2$

. On conclut en utilisant la stricte croissance de la fonction carrée sur $\mathbf{R}^+$

On remarque que $\Im m(z)^2\le \Re e(z)^2+\Im m(z)^2=|z|^2$

. On conclut en utilisant la stricte croissance de la fonction carrée sur $\mathbf{R}^+$

Proposition

Pour tous nombres complexes $z$

et $z'$

, on a :

$|zz'|=|z||z'|$

$\displaystyle\left|\dfrac{z}{z'}\right|=\dfrac{|z|}{|z'|}$

, $z'\neq 0$

Démonstration

Pour tous nombres complexes $z$

et $z'$

$|zz'|^2=zz'\times \overline{zz'}=z\overline{z}\times z'\overline{z'}=|z|^2|z'|^2.$

Pour tous nombres complexes $z$

et $z' \neq 0$

$\displaystyle\left|\dfrac{z}{z'}\right|^2=\dfrac{z}{z'}\overline{\left(\dfrac{z}{z'}\right)}=\dfrac{z\overline{z}}{z'\overline{z'}}=\dfrac{|z|^2}{|z'|^2}.$

Proposition : identité remarquable

Pour tous nombres complexes $z$

et $z'$

$|z+z'|^2=|z|^2+2\Re e(z\overline{z'})+|z'|^2.$

Démonstration

On applique la formule liant module et conjugué :

$\begin{align*} |z+z'|^2 &=(z+z')\overline{(z+z')}\\ &=(z+z')(\overline{z}+\overline{z'})\\ &=z\overline{z}+z\overline{z'}+z'\overline{z}+\overline{z}\overline{z'}\\ &=|z|^2+z\overline{z'}+\overline{z\overline{z'}}+|z'|^2\\ &=|z|^2+2\Re e(z\overline{z'})+|z'|^2. \end{align*}$

Proposition : les inégalités triangulaires

Pour tous nombres complexes $z$

et $z'$

, on a :

$|z+z'|\le |z|+|z'|$

$\displaystyle\left||z|-|z'|\right|\le |z-z'|$

Démonstration

Soient $z$

et $z'$

deux nombres complexes. Alors :

$|z+z'|^2=|z|^2+2\Re e(z\overline{z'})+|z'|^2.$

Or $\Re e(z\overline{z'})\le |z\overline{z'}|$

. Ainsi :

$|z+z'|^2\le|z|^2+2|z\overline{z'}|+|z'|^2=(|z|+|z'|)^2.$

La fonction carrée étant strictement croissante sur $\mathbb{R}^+$

, on en déduit que :

$|z+z'|\le |z|+|z'|.$

On va utiliser l’inégalité que l’on vient de démontrer. Soient $z$

et $z'$

deux complexes :

$|z|=|z-z'+z'|\le |z-z'|+|z'| \text{ et } |z'|=|z'-z+z|\le |z'-z|+|z|.$

Ainsi : $|z|-|z'|\le |z-z'| \text{ et } |z'|-|z|\le |z-z'|.$

En conclusion, $\displaystyle\left||z|-|z'|\right|\le |z-z'|$

Maîtrise la notion de module et la manipulation des nombres complexes pour exceller dans tes études scientifiques grâce à notre cours de soutien scolaire en ligne. ✨

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

5/5 - (1 vote)

Sommaire

Le corps des nombres complexes
Écriture algébrique d’un nombre complexe

Annuler la réponse

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉

Qu’est-ce que le module d’un nombre complexe ?

Le corps des nombres complexes

Quelques prérequis pour comprendre les nombres complexes

Définition de la Loi de composition interne

Construction du corps des complexes

Définition

Démonstration

Écriture algébrique d’un nombre complexe

Partie réelle, partie imaginaire

Définition

Remarque

Proposition

Démonstration

Proposition : Linéarité des parties réelle et imaginaire

Démonstration

Conjugué et module d’un nombre complexe

Définition

Proposition

Proposition

Proposition

Proposition

Proposition

Proposition : identité remarquable

Proposition : les inégalités triangulaires

Annuler la réponse

Annuler la réponse