Qu'est-ce que la puissance d'une matrice ?

Si tu as compris ce qu’était la puissance d’un nombre, alors il n’y a aucune raison que tu ne parviennes pas à comprendre ce qu’est la puissance d’une matrice. Dans ce cours, tu trouveras toutes les définitions et les propositions indispensables pour maîtriser la notion de puissance d’une matrice. Et si malgré tout, les matrices te donnent des maux de tête, nos professeurs d’algèbre t’accompagneront pour que tu puisses les apprivoiser et les manipuler avec aisance. 🧠

📍Définition : Puissance d’une matrice

Soit $A$

une matrice carrée d’ordre $n$

. On définit les puissances successives de $A$

par :

$$A^0 = I_n$ et $\forall k \in \mathbb{N}, A^{k+1} = A^k \times A$.$

Autrement dit,

$$A^k = \underbrace{A \times ... \times A}_{k fois}$.$

Pur tout $k \in \mathbb{N}$

, la matrice $A^k$

est appelée la puissance k-ième de $A$

Exemple : Calculons les puissances de la matrice

$A= \begin{pmatrix} 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

On a : $A^0 = I_4$

, de plus,

$A^2 = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} ,$

$A^3 = \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} ,$

$A^4 = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} .$

Donc, pour tout $n \geq 4, A^n = 0_4 .$

📍 Définition : Matrice nilpotente

Soit $A \in \mathscr{M}_n(\mathbb{K})$

. On dit que $A$

est une matrice nilpotente s’il existe $p \in \mathbb{N}$

tel que $A^p = 0$

. Le plus petit entier $p$

vérifiant $A^p = 0$

est appelé indice de $A$

Remarque : Une matrice strictement triangulaire (supérieure ou inférieure) est nilpotente.

☝️ Proposition :

Soit $A = Diag(\lambda_1,...,\lambda_n)$

une matrice diagonale de $\mathscr{M}_n(\mathbb{K})$

. Avec la convention $0^0 = 1$

, on a, pour tout $k \in \mathbb{N}, A^k = Diag(\lambda_1^k,...,\lambda_n^k)$

Démonstration : On le prouve par récurrence sur $k \in \mathbb{N}$ .

📍Définition :

Soient $A = (a_{i,j})_{1 \leq i, j \leq n} \in \mathbb{M}_n(\mathbb{K})$

et $B = (b_{i,j})_{1 \leq i, j \leq n} \in \mathbb{M}_n(\mathbb{K})$

. On dit que $A$

et $B$

commutent lorsque $AB = BA$

Exemple :

Soit $A \in \mathbb{M}_n(\mathbb{K})$

. On sait que, pour tout $n \in \mathbb{N}, I_n \times A = A \times I_n$

.
Donc, la matrice $I_n$

commute avec toutes les matrices de $\mathbb{M}_n(\mathbb{K})$

. Plus généralement, les matrices scalaires commutent avec toutes les matrices de $\mathbb{M}_n(\mathbb{K})$

On a montré que deux matrices diagonales commutent.

Par récurrence, on montre que : si $A$

et $B$

commutent, alors $B$

commute avec toute puissance de $A$

Les matrices $A= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$

et $B= \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}$

ne commutent pas, en effet :

$AB = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}$

et $BA = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}$

☝️ Proposition : Formule du binôme de Newton

Soient $A \in \mathbb{M}_n(\mathbb{K})$

et $B \in \mathbb{M}_n(\mathbb{K})$

deux matrices qui commutent. Pour tout $N \in \mathbb{N}$

, on a :

$$(A+B)^N = \sum_{k=0}^n \binom{N}{k} A^k B^{N-k}$.$

Démonstration : On prouve cette formule par récurrence sur $N \in \mathbb{N}$ en utilisant la formule de Pascal.

🚨ATTENTION 🚨

La commutativité est indispensable, sans l’hypothèse “A et B commutent”, on ne peut pas appliquer la formule du binôme de Newton !

Par exemple, avec $A= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$

et $B= \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}$

, on a

$(A+B)^2 = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}^2 = \begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}$

et $A^2+2AB+B^2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + 2 \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix} + \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 2 & 1 \end{pmatrix}$

.

Donc, $(A+B)^2 \ne A^2 + 2AB + B^2$

.
Tout ce qu’on peut écrire est : $(A+B)^2 = (A+B)(B+A) = A^2 + AB + BA + B^2$

Remarque : On sait que les matrices scalaires commutent avec toutes les matrices de $\mathscr{M}_n(\mathbb{K})$ . Cette remarque peut faciliter le calcul des puissances de matrices.

Exemple :

Soit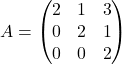 $n \in \mathbb{N}^*$

. Calculer la puissance n-ième de la matrice : $A = \begin{pmatrix} 2 & 1 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{pmatrix}$

.
On pose $N = \begin{pmatrix} 0 & 1 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{pmatrix}$

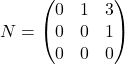de sorte que $A = 2I_3 + N$

. On peut vérifier facilement que la matrice $N$

est nilpotente d’ordre 3, ainsi : $\forall n \geq 3, N^n = 0$

. Les matrices $N$

et $2I_3$

commutent, d’après la formule du binôme de Newton :

$\forall n\in\mathbb{N}, (2I_3+N)^n = \sum_{k=0}^n \binom{n}{k}N^k(2I_3)^{n-k} = 2^nI_3+n2^{n-1}N+ \frac{n(n-1)}{2}2^{n-2}N^2$

.

Notons que : $N^2 = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$

.

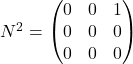On en déduit que : $\forall n\in\mathbb{N}$

, $A^n= \begin{pmatrix} 2^n & n2^{n-1} & n(n-1)2^{n-2} \\ 0 & 2^n & n2^{n-1} \\ 0 & 0 & 2^n \end{pmatrix}$

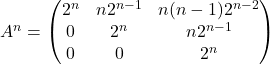📍Définition :

Soient $P \in \mathbb{K}[X]$

tel que $P= \sum_{k=0}^n a_kX^k$

et $A \in \mathscr{M}_n(\mathbb{K})$

.
On définit la matrice $P(A)$

par :

$$P(A) = \sum_{k=0}^n a_kA^k$.$

On dit que $P$

est un polynôme annulateur de $A$

si $P(A) = 0_n$

Exemple :

Soit $M = \begin{pmatrix} -1 & 3 \\ -4 & 6 \end{pmatrix}$

. On a : $M^2 - 5M + 6I_2 = M^2 - 5M + 6M^0 = 0_2$

. On en déduit que le polynôme $P = X^2 - 5X + 6$

est un polynôme annulateur de $M$

Un polynôme annulateur permet notamment de trouver les puissances d’une matrice (voir dans la partie « méthodes pas à pas »).

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

Tu as aimé cet article ?

Qu’est-ce que la puissance d’une matrice ?

Annuler la réponse

Annuler la réponse