Est-ce que 10 est un nombre relatif ? Oui ! Seulement, qu’est-ce qu’un nombre relatif ? Sans le savoir, tu côtoies le nombre relatif depuis tout petit. Sauf que tu ne l’appelleras ainsi qu’à partir de la 5ème. Peu importe ton niveau scolaire -collège, lycée, université- tu te retrouves tôt ou tard confronté à ce chapitre de mathématiques. C’est l’heure de la petite leçon ! ⏰
📜 Les origines du nombre relatif
✔️ Le nombre relatif fait sa première apparition dans les textes indiens – notamment ceux de Aryabhata, grand mathématicien et astronome de l’âge classique en Inde (entre 450 et 550 ans après J.C.).
✔️ En Europe, c’est beaucoup plus tardivement que la notion apparaît – vers le XVIᵉ siècle – avec Simon Stevin, mathématicien et comptable à l’origine de la règle des signes dans le calcul de deux entiers relatifs.

La leçon sur le nombre relatif
📘 La définition du nombre relatif
Le nombre relatif est aussi connu sous d’autres noms comme entier relatif, entier rationnel ou encore simplement nombre entier.
👉 De manière générale, il s’agit d’un nombre, ou d’un chiffre, entier, sans virgule, auquel on a ajouté un signe positif + ou négatif –. Il indique la distance d’une valeur à zéro, le point neutre.
Par exemple : Tu mesures 1,56 m, soit, 156 cm. Le point neutre (0), c’est le sol. Tu te situes donc à +156 cm du sol. +156 est ici un nombre relatif.
👉 On appelle opposé au nombre relatif, son équivalent négatif.
Par exemple : L’opposé de +156 cm est -156 cm. Soit 1,56 mètre sous la terre.
🚨 Attention
❌ Ne confonds pas :
- un entier rationnel qui est un nombre relatif comme 2, 10, -60
avec :
- un nombre relatif qui est un nombre exprimé en quotient sous la forme de fraction comme ½.
À lire aussi
✅ Comment vaincre la peur des maths ?
🤙 Les règles d’utilisation des signes
Le nombre relatif au cœur des additions et des soustractions 🤓
📍 La somme de deux nombres relatifs de même signe, qu’il soit positif ou négatif, se calcule en additionnant les valeurs. On garde le signe commun pour le résultat final.
Exemples :
- Calculons (+4)+(+3)
Ici, on a le même signe +. On peut donc simplifier l’expression :
(+4)+(+3)
= 4+3
= 7
= + 7
- Calculons (-24)+(-23)
= 24 + 23
= 47
= – 47
📍 Si les deux nombres relatifs sont de signe différent, on calcule la différence en gardant au résultat final le signe dont la valeur est plus grande.
🚨 Règle d’utilisation
Dans certains cas, l’accumulation des signes peut t’induire en erreur. Pour éviter les faux calculs, voici les règles de sélection pour les signes qui se suivent :
➕ par ➕ = ➕
➖ par ➖ = ➕
➕ par ➖ = ➖
➖ par ➕ = ➖
Exemples :
- Calculons (+11) – (- 8)
= 11 + 8
= 19
- Calculons -6 – (+2)
= -6 -2
= -8
À lire aussi
✅ Tout savoir sur le programme de maths en 5ème !
Le nombre relatif et la multiplication 😎
Le produit d’une multiplication –son résultat– est obtenu en faisant le produit des valeurs absolues des nombres relatifs et en respectant les règles des signes.
🧐 Qu’est-ce qu’une valeur absolue ?
Une valeur absolue correspond à la valeur réelle d’un nombre sans tenir compte de son signe.
Autrement dit :
- -6 = 6
- +8 = 8.
Exemples :
- (+2) x (+5) = 2 x 5 = 25
- (+2) x (-5) = 2 x (-5) = -25
- (-2) x (+5) = (-2) x 5 = -25
- (-2) x (-5) = 25
+ / + = +
+/- = –
-/+ = –
-/- = +
À lire aussi
✅ Tout savoir sur le programme de maths de 4ème !
Le nombre relatif et la division 😨
On sait que la division est une opération en mathématique difficile pour beaucoup d’élèves. La division des nombres relatifs va te faire changer d’avis ! 🤗
Lors d’une division de deux nombres relatifs, il y a deux règles :
- si les nombres ont le même signe, le résultat est positif
- si les nombres ont un signe différent, le résultat est négatif
Exemples :
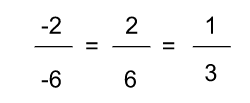
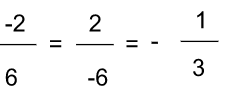

À lire aussi
✅ Tout savoir sur le programme de maths de 3ème !
À quoi sert un nombre relatif ? 🧐
Faire la différence entre deux entiers naturels 🤷
Un entier naturel est un nombre permettant de calculer la quantité d’un objet ou d’un élément. Faire la différence entre deux entiers naturels, c’est pouvoir les comparer et ça passe par le nombre relatif.
Ils permettent de répondre à une inconnue comme X ou Y, de comparer des situations ou d’énumérer la quantité d’un produit.
Définir une position sur un axe ↘️
En cours de mathématiques, tu trouveras la plupart du temps un exercice de nombre relatif avec son positionnement sur un axe gradué, comme ceci 👇
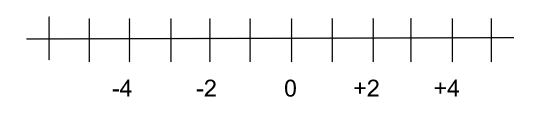
Sur un axe gradué, on appelle une valeur associée à un point une abscisse. Autrement dit, là où l’axe est coupé.
Exemple :
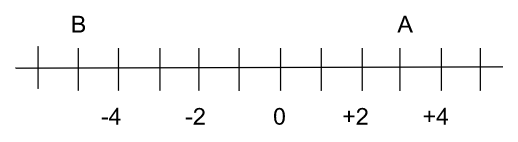
L’abscisse de A est +3, on l’écrit A(3).
L’abscisse du point B est -5, on l’écrit B(-5).
L’axe te permet également de pouvoir comparer les valeurs : A > B
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
✒️ Exercices
- Addition et soustraction des nombres relatifs
Calcule les expressions suivantes :
(+4) + (-9)
(-8)+(-11)+(+24)
(-24)-(-11)-(+4)
(-2000)-(-666)
- Multiplication et division d’un nombre relatif
(+5) x (+11)
(-4) x (+5)
-1/-21
24/44
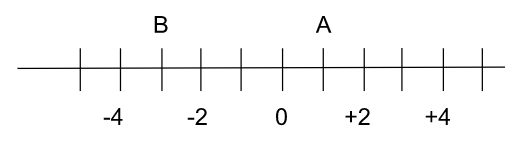
- Lire une échelle graduée
Trouve les abscisses des points A et B.
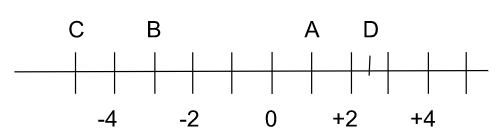
Place le point C en -5 et le point D en +2,5.
Compare les points A et B, C et D, puis rangent les points par ordre croissant.
Corrections ✔️
1 –
(+4) + (-9) = 4 – 9 = -5
(-8)+(-11)+(+24) = (-19) + 24 = +5
(-24)-(-11)-(+4) = -24 + 11 – 4 = – 28 + 11 = – 17
(-2000)-(-666) = – 2000 + 666 = – 1334
2 –
(+5) x (+11) = 5 x 11 = 55
(-4) x (+5) = – 20
-1/-21 = 1/21
24/-44 = – 24/ -44
3 –
A(1) ; B(-3)
A>B ; C<D ⇒ D > A > B > C

Cette fiche de cours de mathématiques spécial nombre relatif est à présent terminée. Ce chapitre n’aura désormais plus aucun secret pour toi. N’oublie pas de nous dire en commentaire si tu as réussi les exercices ! 🤩