C’est l’arrivée au lycée, tu vas croiser de nouvelles têtes et faire des rencontres qui marqueront à jamais ta vie. 🔥
Mais pas si vite, Madame Benoît, ta prof de maths, compte sur toi pour que tu connaisses sur le bout des doigts la notion d’intersection. 😮
Bah oui, il ne faudrait pas la décevoir quand même. Bon allez, on va t’en dire plus sur l’intersection et tout ce qui en découle ! ✍️
L’intersection, c’est quoi ? 🤔
L’intersection, c’est le lieu de rencontres de deux choses. Mais qu’est-ce que cela signifie vraiment en mathématiques ?
L’intersection en maths 📚
Alors déjà, il faut savoir que cette notion ne sera pas seulement abordée en Seconde mais aussi plus tard au lycée, jusqu’à la Terminale.
En effet, ce qu’on va voir aujourd’hui, c’est plutôt un focus sur l’intersection de deux évènements en maths, les probabilités et les intersections d’intervalles. 👀
Mais sache que tu auras l’occasion de reparler d’intersection en géométrie, mais plus tard dans le programme (en Terminale). Tu vas traiter des intersections entre une droite et un plan, entre deux droites, etc. et tu auras le plaisir de voir tout un tas de formules, d’équations et de fonctions qui font mal à la tête (bonne chance à toi du futur). 🍀

À lire aussi
Tu veux tout savoir sur les calculs littéraux ? Regarde cet article ! 🔡
Ton premier cours particulier est offert ! 🎁
Nos profs sont passés par les meilleures écoles et universités.
Intersection de deux ensembles 🗨️
Place à ce qui nous intéresse et à quelques éléments de définition. Dans la théorie des ensembles, l’intersection de deux ensembles A et B se note A∩B et désigne simplement l’ensemble des éléments qui appartiennent, à la fois, à A et à B. C’est l’ensemble des éléments communs de A et de B.
D’ailleurs, la notation A∩B, on la lit « A inter B » et pour tout x, on écrit : x ∈ A∩B si (si et seulement si) x ∈ A et x ∈ B. Voici un joli diagramme de Venn pour que tu saisisses à quoi correspond A∩B.

Eh oui, l’élément « x » appartient à l’intersection de A et de B seulement si celui-ci se trouve à la fois dans l’ensemble A et dans l’ensemble B, sinon ce n’est pas logique. 🤷

❌ Événements incompatibles
En probabilité, on dit que deux événements sont disjoints ou incompatibles lorsque A∩B = ∅ (l’intersection est vide).
Intersection des événements 🧠
Maintenant qu’on a vu les éléments de langage essentiels, place à un peu plus de concret avec l’application de cette notion dans le monde des probabilités et plusieurs exercices.
Les probabilités 🔢
💡 Un événement de probabilité, c’est quoi ?
La probabilité d’un événement (la proba que quelque chose se produise) est comprise entre 0 et 1. Si elle est de 0, l’événement est considéré comme impossible (ça n’arrivera jamais). Si la probabilité est de 1, alors on est 100 % que l’événement se produira.
Quant à l’événement intersection de A et B (A∩B), il est réalisé, lorsque les deux événements A et B sont réalisés de façon simultanée.
Petits exemples et exercices pour que tu comprennes mieux : premièrement, prends un paquet de 52 cartes avec :
A : « On tire un sept » 7️⃣
B : « On tire une carte carreau » ♦️
Quel est A∩B ? Et bah, A∩B est : « on tire un sept de carreau ». Si on veut que A et B se réalisent en même temps, la seule solution est le sept de carreau. ✅
Maintenant que tu as compris le truc, on va passer à des calculs de probabilités. Ne panique pas, ça va bien se passer (enfin, on espère). 😨

Deuxième exemple complémentaire : on lance simultanément deux dés (un vert et un bleu) à 6 faces non-truqués (pas de triche oh), avec les évènements suivants :
A : « La somme des points obtenus est égale à 2. »
B : « La somme des points obtenus est égale à 5. »
C : « Le dé vert s’arrête sur le chiffre 3. »
📝 Calcul probabilités
Calculons les probabilités des trois événements.
P(A) = 1/36. Pourquoi ? La seule possibilité est que le dé vert fasse 1 et le dé bleu aussi (donc une chance sur 6 à chaque fois) donc P(A) = 1/6 * 1/6 = 1/36.
P(B) = 4/36 = 1/9. On a, en effet, quatre possibilités que cela arrive : le dé vert fait 1 et l’autre 4, le dé vert fait 2 et le bleu 3, le bleu fait 1 et le vert 4 puis le bleu fait 2 et le vert 3.
P(C) = 1/6. Là, c’est simple, on ne s’occupe pas du dé bleu, il n’intervient pas dans l’événement, tout ce qu’on veut, c’est que l’autre tombe sur le 3. Et pour cela, il y a une chance sur 6.
Quelle est donc la probabilité de l’intersection des événements B et C ? Eh bah P(B∩C) = 1/36 car on doit obtenir 5 et le dé vert doit faire 3. Donc la seule solution c’est que, d’un côté, le dé vert fasse 3 et le dé bleu fasse 2.
À lire aussi
Voici 7 films qui vont te faire aimer les maths ! 🍿
Ne pas confondre l’intersection avec… 🥴
L’intersection (quand A et B se réalisent) n’est pas la seule possibilité et il ne faut pas la confondre avec la réunion et l’événement contraire.
La réunion 🫂
L’événement réunion de A et B, qui se note A∪B (on le lit A union B), se produit lorsqu’au moins un de deux événements se produit. On sait qu’une définition ne suffit pas toujours et que tu apprécies les diagrammes, donc en voici un nouveau :
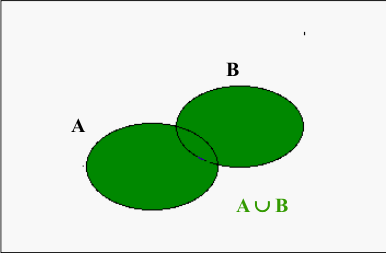
Reprenons l’exemple du paquet de 52 cartes avec A : « On tire un sept » et B : « On tire une carte carreau ». Dans ce cas-là, A∪B c’est « on tire le sept de coeur, le sept de trèfle, le sept de pique ou un carreau. » 🃏

🚨 Propriété
P(A∪B) = P(A) + P(B) – P(A∩B). On enlève P(A∩B) car on intègre deux fois l’intersection A∩B quand on prend l’événement A puis le B (la zone verte sur le schéma).
D’ailleurs, si tu as bien suivi, tu devrais savoir que si A et B sont incompatibles, P(A∪B) = P(A) + P(B) car P(A∩B) = ∅.
L’évènement contraire 🙃
Définition simple mais efficace : l’événement contraire de A est celui qui se réalise lorsque A, lui, ne se réalise pas. On le note A‘.
↪️ Propriété
En toute logique, la somme de la probabilité de l’événement A et de celle de son contraire est égale à 1. Donc P(A) + P(A’) = 1.
Tu fais une petite équation dans ta tête et tu comprends donc que P(A’) = 1 – P(A).
Passons maintenant à un exemple pour que tu intègres bien la notion d’événement contraire. Tu as 3 boules dans un saladier. Une rouge, une blanche et une noire puis tu en tires une seule. On considère l’événement A : « tirer la boule rouge » donc A’ : « tirer la boule blanche ou noire » 🔴
C’est un cas d’équiprobabilité, c’est-à-dire que la probabilité de tirer chaque boule est la même (une chance sur trois). On a donc A = {Rouge}, d’où P(A) = 1/3.
Conclusion : P(A’) = 1 – P(A) = 2/3.
D’ailleurs, on aurait pu prendre le problème différemment dans ce cas. On décompose A’ en deux événements B : « tirer la boule blanche » et C : « tirer la boule noire ». ⚪⚫
On calcule la réunion de B et C, ce qui nous donne P(A’) = P(B∪C) = P(B) + P(C) – P(B∩C) = 1/3 + 1/3 = 2/3. Il ne faut pas oublier que l’intersection B∩C est vide car les deux événements sont incompatibles (on ne peut pas tirer la boule noire et la boule blanche en même temps vu qu’on en tire qu’une seule). 👏
À lire aussi
Un peu de SVT tiens. On t’explique tout sur la plaque tectonique ! 🌋
Besoin d’un prof particulier ? ✨
Nos profs sont là pour t’aider à progresser !
Intersection des intervalles👁️🗨️
On va quitter les probabilités et on va parler des intervalles cette fois. Un intervalle, en maths, est un ensemble ordonné de points compris entre deux bornes. On va te présenter deux exemples concrets pour que tu comprennes mieux. 👉
1️⃣ Prenons les intervalles I = [-2 ; 2] et J = ]-3 ; 1[. Dès lors, quelle est l’intersection de I et J ? Déterminer cette intersection, c’est déterminer tous les nombres qui appartiennent à la fois à I et à J.
Voici un axe gradué pour mieux comprendre :
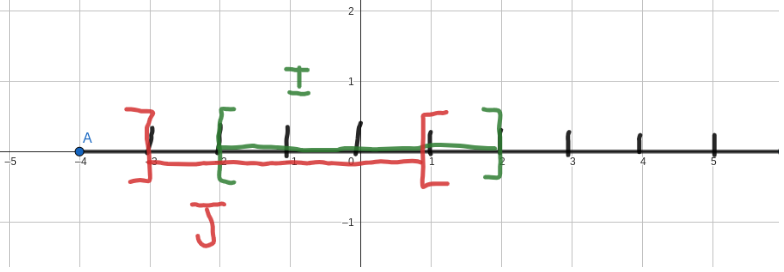
Cette intersection on la trouve dans la zone qui est à la fois marquée de vert et de rouge. Il semblerait que ce soit -2 ; 1.
Maintenant, attention aux bornes ! -2 est compris dans I car la bornes est fermée et dans J aussi (car J va jusqu’à -3) et 1 est dans I car l’intervalle va jusqu’à 2 mais que 1 n’est pas compris dans J car la borne est ouverte.
Ce qui nous donne donc : I∩J = [-2 ; 1[.
2️⃣ On a les intervalles I = ]-∞ ; -2] et J=[0 ; 4]. On a donc l’axe gradué suivant :
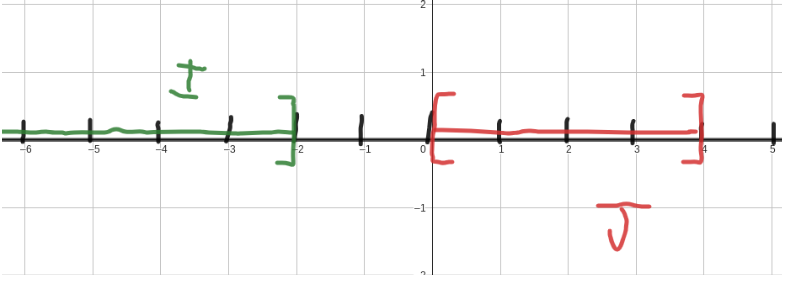
On cherche tous les nombres qui appartiennent à la fois à l’intervalle I et dans le même temps à l’intervalle J. Mais on remarque que les deux intervalles ne se chevauchent en aucun cas. Dans ce cas, on note l’intersection de la façon suivante : I∩J = ∅.
À lire aussi
Teste ta logique mathématiques avec ce quiz ! 🧠
Bon on espère que nos explications, nos exercices et nos jolis dessins pour te modéliser les intervalles t’auront plus. 🖌️

En tout cas, tu ne pourras plus dire que tu ne connais rien aux intersections. Essaye de calculer la probabilité que tu as d’avoir la moyenne en maths cette année et tiens-nous au courant. 😉
Et si tu as toujours des difficultés dans cette matière, n’hésite pas à prendre des cours de maths en ligne avec l’un de nos Sherpas ! 😀















Dans la propriété qui donne la probabilité de la réunion de deux événements :
P(A∪B) = P(A) + P(B) car P(A∩B) = ∅,
il faut remplacer ∅ par 0.
Et insister sur le fait que P(∅)=0, mais que ∅ et 0 ne sont pas de la même nature : Le premier est un ensemble tandis que le second est un nombre 🙂