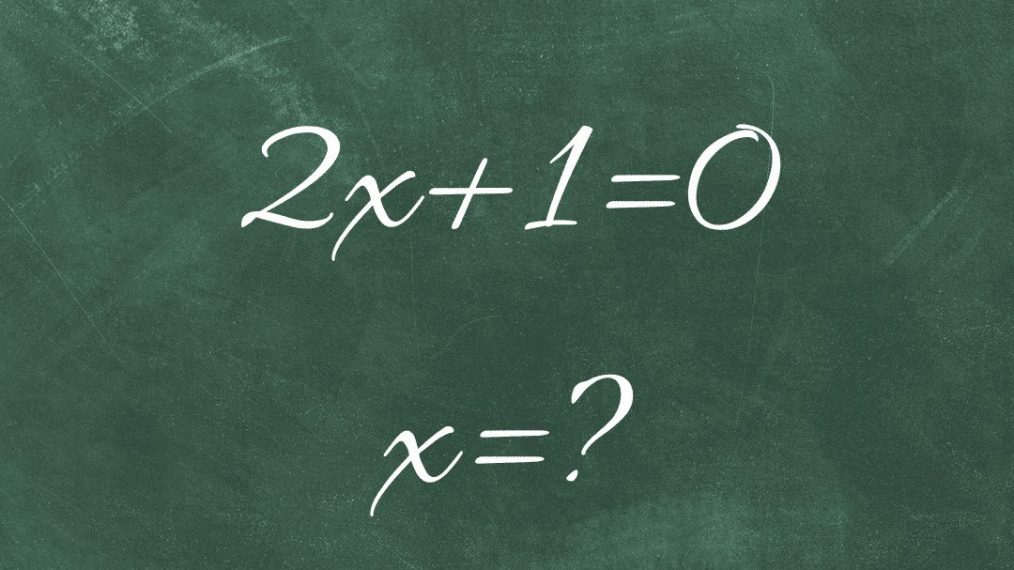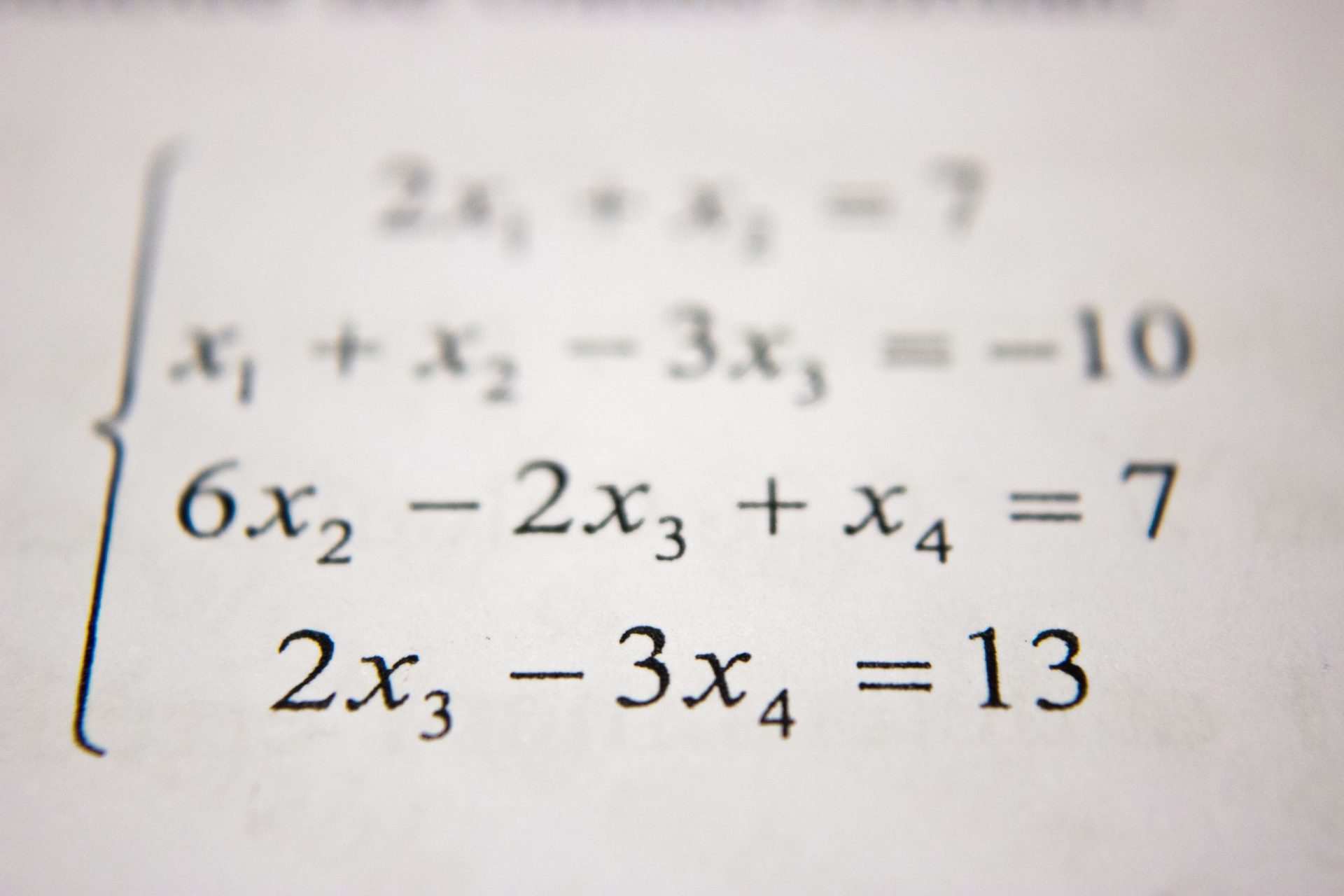🧮 Équation et inéquation : comment les résoudre ? Sherpas

S’il y a une notion à laquelle tu auras affaire en maths, c’est bien l’équation, mais aussi l’inéquation ! Aujourd’hui, on te propose une fiche de cours dessus. De leur définition à leur résolution en passant par leurs différences, tu sauras tout. Prêt à résoudre le mystère des équations et des inéquations ? C’est parti ! 🚀

Un exercice de maths qui demande de trouver x et la personne fais une flèche jusqu'à x. — *Quand tu devais trouver « x » avant de connaître les Sherpas !*

Équation et inéquation, c’est quoi ? 👀

Définitions 📖

Selon le Robert, une équation est une “relation d’égalité qui n’est vérifiée que pour certaines valeurs de la variable, appelée inconnue”, et une inéquation est une “inégalité conditionnelle existant entre deux quantités et dépendant de certaines variables (ou inconnues)”.

Un peu de vocabulaire 📒

Homer Simpson qui regarde dans un dictionnaire.

Inconnue

L’inconnue d’une équation ou d’une inéquation est un nombre que tu ne connais pas. C’est celui que tu cherches à déterminer.

$4\underline{x}+5=8$

Signe

« $=$ » $\textit{égal}$ pour les équations.

« $>$ » $\textit{supérieur à}$ ; « $<$ " $\textit{inférieur à}$ ; " $\leq$ " $\textit{inférieur ou égal à}$ ; " $\geq$ " $\textit{supérieur ou égal à}$ pour les inéquations.

$4x+5\underline{=}8$

$4x+5{\underline{\leq}8$

Membre

Une équation (ou une inéquation) est séparé par deux membres.

$\underline{4x+5}=\underline{8}$

$\underline{8x+7}>\underline{2x+1}$

Équation ou inéquation, quelle différence ? 🤔

Un homme demande quelle est la différence. — *On te le dit tout de suite !*

La chose la plus évidente qui différencie une équation d’une inéquation est leur signe (égalité ou inégalité) entre les deux expressions.

↪️ Exemple :

$2x+1=7$ est une équation alors que $2x+1>7$ est une inéquation.

Globalement, les règles pour les inéquations sont les mêmes que pour les équations, sauf dans deux cas !

1er cas : quand on multiplie ou qu’on divise par un nombre négatif, on change le signe de l’inéquation.

↪️ Exemple :

$-4x>5$
$x<\dfrac{5}{-4}$

2e cas : quand on inverse, on change de signe.

↪️ Exemple :

$\dfrac{1}{x}>3$
$\dfrac{x}{1}<\dfrac{1}{3}$

Personne qui donne des cours particuliers

Tu as des lacunes en maths ? Prends des cours particuliers avec un de nos Sherpa !

Les types d’équations et d’inéquations 📜

Un homme compte avec ses doigts entouré d'équations. — *Quand on te demande combien il y a de types d’équations*

Équation et inéquation du premier degré

Une équation du premier degré est une équation de la forme $ax=b$ avec $x$ l’inconnue.

↪️ Exemple

$5x=3$ est une équation du premier degré.

Équation du second degré

Une équation du second degré est une équation de la forme $ax^2+bx+c=0$ .

↪️ Exemple

$3x^2+4x-5=0$ est une équation du second degré car ici $a=3$ ; $b=2$ ; $c=-5$

Tu paniques parce que tu ne comprends toujours rien. N’hésite pas à prendre des cours particuliers de maths en ligne avec l’un de nos Sherpas !

Équation produit

Une équation produit est de la forme $f(x)\times{g(x)}=0$

↪️ Exemple

$(2x+9)(5x-4)=0$ est une équation produit.

Équation quotient

Une équation produit est de la forme $\dfrac{f(x)}{g(x)}=0$

↪️ Exemple

$\dfrac{2x+5}{4x-1}=0$ est une équation quotient.

⚠️ N.B.

Quand on parle de types d’équations ici, on parle également des inéquations !

Noémie

M2 en droit à Assas

19€/h

Fanny

Ponts ParisTech

19€/h

Antoine

Sciences Po Paris

18€/h/h

Hugo

Insa Lyon

16€/h

Margot

Arts et Métiers ParisTech

22€/h/h

Olivier

La Sorbonne

13€/h

Clémence

HEC Paris

21€/h/h

Nicolas

CentraleSupélec

17€/h

Ton premier cours particulier est offert ! 🎁

Nos profs sont passés par les meilleures écoles et universités.

J’EN PROFITE MAINTENANT !

Comment modéliser une équation ou une inéquation ? 🧐

Modéliser une équation ou une équation signifie traduire un énoncé. On t’explique avec des exemples pour que tu comprennes mieux !

Exemple 1

Énoncé

On a un rectangle de périmètre égal à 25 cm et de longueur égale à 7 cm. Quelle est la largeur de ce rectangle ?

Modélisation

💡 Rappel

Formule du périmètre d’un rectangle :
P_rectangle=Longueur+largeur+Longueur+largeur
P_rectangle=(L+l)×2

On a donc : $25=(7+l)\times2$

L’inconnue ici est « $l$ « .

Résolution

$25=14+2l$
$25-14=2l$
$11=2l$
$5,5=l$

Exemple 2

Énoncé

Tom se rend au marché avec 12 euros en poche et doit acheter des pommes. Sachant qu’une pomme coûte 1,10 euros, combien de pommes Tom peut-il acheter ?

Modélisation

$1,10x\leq12$

$x$ représente le nombre de pommes. Il te faut trouver $x$ pour que Tom ne dépasse pas son budget de 12 euros.

Résolution

Note bien ici que Tom ne peut acheter que des pommes entières. Ici Tom peut acheter 1 à 10 pommes pour respecter la condition inférieure ou égale.

Une femme écrit des formules mathématiques au tableau et des hommes regardent. — *Comment tu te sens quand tu modélises une équation*

Comment résoudre une équation et une inéquation ? 🤓

Résoudre une équation ou une inéquation, qu’est-ce que ça veut dire ?

Résoudre une équation ou inéquation, c’est trouver sa solution et donc le nombre inconnu pour lesquelles l’égalité ou l’inégalité est vraie.

Méthodes pour résoudre une équation ou une inéquation

Tester

Si l’équation est relativement simple, tu peux tester différentes solutions.

↪️ Exemple

$7x=42$

Si tu connais bien tes tables de multiplication, tu sais que :

$7\times6=42$

Donc la solution est 6.

Isoler l’inconnue

Pour y voir plus clair, le mieux est d’isoler l’inconnue !

Pablo Escobar seul. — *Quand tu as bien isolé l’inconnue*

↪️ Exemple

$5x+7=5-8x$

Étape 1 : on met tous les x d’un côté et toutes les constantes de l’autre

$5x+8x=5-7$

Étape 2 : on calcule

$5x+8x=5-7\iff13x=-2$

Étape 3 : on résout

$13x=-2$

$x=\dfrac{-2}{13}$

↪️ Exemple

$2x+6>7x-3$

Étape 1 : on met tous les x d’un côté et toutes les constantes de l’autre

$2x-7x>-3-6$

Étape 2 : on calcule

$-5x>-9$

Étape 3 : on résout

$x<\dfrac{-9}{-5}$

$x<\dfrac{9}{5}$

⚠️ Attention

On divise par un nombre négatif, alors il faut changer le sens de l’inégalité !

Supprimer les parenthèses

Si tu fais face à une équation avec des parenthèses, la développer peut t’aider à la résoudre.

↪️ Exemple

$5(x+4)=-(x+7)+3$

$5x+20=-x-7+3$

$5x+20=-x-4$

$5x+x=-4-20$

$6x=-24$

$x=-4$

Cas d’une équation produit nulle

Si une équation produit est nulle alors un des facteurs est nul.

↪️ Exemple

$(2x+6)(4-9x)=0$

$2x+6=0$ ou $4-9x=0$

1er cas :

$2x+6=0$

$2x=-6$

$x=\dfrac{-6}{2}$

$x=-3$

2e cas :

$4-9x=0$

$-9x=-4$

$9x=4$

$x=\dfrac{4}{9}$

Étudier le signe d’une inéquation

↪️ Exemple

$\dfrac{2x+6}{4-2x}\leq0$

L’équation n’est pas définie pour $4-2x=0$ et donc pour $x=2$

$2x+6=0$

$x=-3$

On résume dans un tableau de signes :

L’ensemble des solutions : $\rbrack{-{\infty};-3}\rbrack{\bigcup}\rbrack{2;+{\infty}\lbrack$

Calculer le discriminant

Pour résoudre un polynôme du second degré, tu dois suivre plusieurs étapes !

Définition

Une équation du second degré est une équation de la forme $ax^2+bx+c=0$ où $a$ , $b$ et $c$ sont des réels avec $a\neq0$

Une solution de cette équation s’appelle une racine du trinôme $ax^2+bx+c$
On appelle discriminant du trinôme $ax^2+bx+c$ , le nombre réel, noté $\Delta$
$\Delta=b^2-4ac$ .

Résolution

Si $\Delta>0$ alors $ax^2+bx+c=0$ a deux solutions distinctes :
$x_1=\dfrac{-b-\surd{Delta}}{2a}$
$x_2=\dfrac{-b+\surd{Delta}}{2a}$

Si $\Delta=0$ alors $ax^2+bx+c=0$ a une unique solution :
$x_0=\dfrac{-b}{2a}$

Si $\Delta<0$ alors $ax^2+bx+c=0$ n’a pas de solution.

↪️ Exemple

$2x^2-3x+1=0$

$a=2$ ; $b=-3$ ; $c=1$

$\Delta=(-3)^2-4(2)(1)=9-8=1$

$\Delta=1$

$\Delta>0$

L’équation admet donc 2 solutions distinctes :

$x_1=\dfrac{-(-3)-\surd{1}}{2\times2}$

$x_1=\dfrac{3-1}{4}$

$x_1=\dfrac{2}{4}$

$x_1=\dfrac{1}{2}$

$x_2=\dfrac{-(-3)+\surd{1}}{2\times2}$

$x_2=\dfrac{3+1}{4}$

$x_2=\dfrac{4}{4}$

$x_2=1$

$S={\dfrac{1}{2};1}$

Clémence

HEC Paris

21€/h/h

Thibault

ENS Paris Ulm

20€/h

Sophie

Sciences Po Bordeaux

12€/h

Noémie

M2 en droit à Assas

19€/h

Fanny

Ponts ParisTech

19€/h

Simon

4e année de médecine

26€/h

Nicolas

CentraleSupélec

17€/h

Victor

ESCP

25€/h

Besoin d’un prof particulier ? ✨

Nos profs sont là pour t’aider à progresser !

JE PRENDS UN COURS GRATUIT !

Exercices ✍️

À toi de jouer maintenant !

Exercice 1

Résous ces équations :

1) $2x^2=6$
2) $7(x-1)=(x+2)+6$
3) $x^2-2x+1=0$
4) $\dfrac{3x-6}{x-1}=0$

Exercice 2

Résous ces inéquations :

$3x+2<5-4x$
$2(4-3x)\geq7x+10$

Corrigés 💯

On espère que ça n’a pas été trop compliqué pour toi ! Voici la correction.

Correction 1

1) Comme x est au carré, nous avons deux solutions : $S={-3;3}$

2) On développe puis on isole x :
$7(x-1)=(x+2)+6$
$7x-7=4x+8+6$
$7x-7=4x+14$
$7x-4x=14+7$
$11x=21$
$x=\dfrac{21}{11}$

3) On calcule le discriminant :
a=1 ; b=-2; c=1
$\Delta=(-2)^2-4(1)(1)=0$
Il y a donc 1 solution :
$x_0=\dfrac{-(-2)}}{2(1)}=1$

4) Pour $x\neq1$ , l’équation $\dfrac{3x-6}{x-1}$ équivaut à $3x-6=0$

$3x=6$
$x=\dfrac{6}{3}$
$x=2$

Correction 2

1) On isole les $x$ :
$3x+4x<5-2$
$7x<3$
$x<\dfrac{3}{7}$
$x\in\rbrack-{\infty};\dfrac{3}{7}\lbrack$

2) On développe et isole les x :
$2(4-3x)\geq7x+10$
$8-6x\geq7x+10$
$-6x-7x\geq10-8$
$-13x\geq2$
$-13x\leq\dfrac{2}{-13}$

Un homme fait des maths et trouve ça simple. — *Toi depuis que tu connais les Sherpas !*

Voilà, notre fiche de cours sur les équations et les inéquations touche à sa fin. Si tu as eu trop de difficultés, n’hésite pas à prendre des cours particuliers en maths avec un de nos Sherpas !

5/5 - (3 votes)

Équation et inéquation : comment les résoudre ? 🔢

Équation et inéquation, c’est quoi ? 👀

Définitions 📖

Un peu de vocabulaire 📒

Inconnue

Signe

Membre

Équation ou inéquation, quelle différence ? 🤔

Les types d’équations et d’inéquations 📜

Équation et inéquation du premier degré

Équation du second degré

Équation produit

Équation quotient

Comment modéliser une équation ou une inéquation ? 🧐

Exemple 1

Énoncé

Modélisation

Résolution

Exemple 2

Énoncé

Modélisation

Résolution

Comment résoudre une équation et une inéquation ? 🤓

Résoudre une équation ou une inéquation, qu’est-ce que ça veut dire ?

Méthodes pour résoudre une équation ou une inéquation

Tester

Isoler l’inconnue

Supprimer les parenthèses

Cas d’une équation produit nulle

Étudier le signe d’une inéquation

Calculer le discriminant

Exercices ✍️

Exercice 1

Exercice 2

Corrigés 💯

Correction 1

Correction 2

Annuler la réponse

Annuler la réponse