Qu'est-ce qu'un espace vectoriel ?

Si tu cherches la définition d’un espace vectoriel, c’est ici ! Tu trouveras également des propositions mathématiques de base ainsi que des conseils méthodologiques pour réussir ta prochaine interro à coup sûr. Grâce à ce cours, apprends tout ce qu’il y a à savoir sur l’espace vectoriel !

Avant de te lancer dans ton prochain devoir sur les vecteurs, renforce tes connaissances avec l’aide d’un Sherpa expert en mathématiques, pour une maîtrise parfaite. ✨

NB : Dans tout le chapitre, $\mathbb{K}$

désigne le corps $\mathbb{R}$

ou $\mathbb{C}$

📍Définition : Espace vectoriel

Soit $E$

ensemble muni :

d’une loi de composition interne notée « + » : c’est-à-dire, une application :

$E \times E \rightarrow E$

$(u,v) \mapsto u+v$

Cette loi est aussi appelée addition.

d’une loi externe notée « . » : c’est-à-dire, une application :

$\mathbb{K} \times E \rightarrow E$

$(\lambda,u) \mapsto \lambda.u.$

Cette loi est aussi appelée multiplication par un scalaire.

On dit que ( $E$

,+,.) est un $\mathbb{K}$

-espace vectoriel (ou $\mathbb{K}$

-ev) lorsque :

( $E$

,+) est un groupe abélien.

La loi « . » est distributive par rapport à l’addition de $E$

$\forall \lambda \in \mathbb{K}, \forall (u,v) \in E^2, \lambda.(u+v) = \lambda.u + \lambda.v.$

la loi « . » est distributive par rapport à l’addition de $\mathbb{K}$

$\forall (\lambda,\mu) \in \mathbb{K}^2, \forall u\in E, (\lambda+\mu.u) = \lambda.u + \mu.u.$

Pour tout $(\lambda,\mu) \in \mathbb{K}^2$

et $u\in E$

, on a : $(\lambda\times\mu).u = \lambda.(\mu.u)$

1 vérifie : $\forall u \in E$

, $1.u = u$

📍Définition :

Les éléments de $E$

sont appelés vecteurs et les éléments de $\mathbb{K}$

sont appelés scalaires.

Remarques :

Pour alléger les notations, on écrit parfois $E$

au lieu de ( $E$

,+,.), et, s’il n’y a pas d’ambiguïté sur le corps $\mathbb{K}$

, on dit que $E$

est un espace vectoriel.

L’élément neutre pour la loi + est noté $0_E$

et est appelé $vecteur\:nul$

Par définition, ( $E$

,+) est un groupe. Pour tout $x \in E$

, il existe donc un unique vecteur $x' \in E$

tel que $x+x' = x'+x = 0_E$

. On note $x' = -x$

et on dit que $x'$

est $l'opposé$

du vecteur $x$

(pour la loi +).

Pour x et y deux vecteurs, on note $x-y = x+(-y)$

Exemple :

L’ensemble $\mathbb{R}^2$

des couples $(x_1,x_2)$

de réels $x_1$

et $x_2$

est muni des opérations suivantes : pour tous vecteurs $(x_1,x_2) \in \mathbb{R}^2$

et $(y_1,y_2) \in \mathbb{R}^2$

, et tout scalaire $\lambda \in \mathbb{R}$

$(x_1,x_2) + (y_1,y_2) = (x_1+y_1,x_2+y_2)\enspace et\enspace \lambda.(x_1,x_2) = (\lambda x_1,\lambda x_2).$

On vérifie alors que $(\mathbb{R}^2,+,.)$

est un $\mathbb{R}$

-espace vectoriel et que son vecteur nul est = $0_{\mathbb{R}^2} = (0,0)$

💡Conseils méthodologiques :

La notion d’espace vectoriel est une notion abstraite. Pour se l’approprier et comprendre les concepts, on s’appuie largement sur des illustrations dans $\mathbb{R}^2$

, ou dans $\mathbb{R}^3$

Exemple :

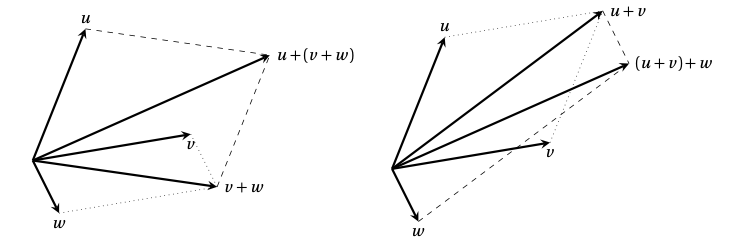
Le schéma suivant illustre l’associativité de l’addition de $E$ .

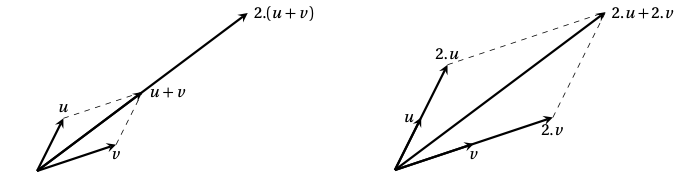
Le schéma suivant illustre la distributivité de la multiplication externe par rapport à l’addition de $E$ .

☝️Proposition :

Démonstration :

Soit ( $E$

,+,.) un $\mathbb{K}$

-espace vectoriel. Pour tous $u\in E$

et $\lambda \in \mathbb{K}$

, on a :

$0.u = 0_E$

;

$\lambda.0_E = 0_E$

;

$(-\lambda).u = \lambda.(-u) = -\lambda.u$

;

$\lambda.u = 0_E$

si, et seulement si, $\lambda = 0$

ou $u=0_E$

Par distributivité, on a : $0.u = (0+0).u = 0.u + 0.u$

. Donc, en ajoutant $-0.u$

de part et d’autre de l’égalité, il vient $0.u = 0_E$

Par distributivité, on a : $\lambda.0_E = \lambda.(0_E+0_E) = \lambda.0_E + \lambda.0_E$

. Donc, en ajoutant $-\lambda.0_E$

de part et d’autre de l’égalité, il vient $\lambda.0_E = 0_E$

On a : $(-\lambda).u + \lambda.u = (-\lambda + \lambda).u = 0.u = 0_E$

. Donc, par unicité de l’opposé, $(-\lambda).u = -\lambda.u$

.
L’égalité $\lambda.(-u) = \lambda.u$

se montre de la même manière.

L’implication réciproque est une conséquence des deux premiers points.
Montrons l’implication directe. On suppose que $\lambda.u = 0_E$

.
– Cas 1 : $\lambda = 0$

. Il n’y a rien à faire.
– Cas 2 : $\lambda \ne 0$

. On a $u = \frac{\lambda}{\lambda}.u = \frac{1}{\lambda}.(\lambda.u) = \frac{1}{\lambda}.0_E$

. Donc, $u=0_E$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

5/5 - (1 vote)

Qu’est-ce qu’un espace vectoriel ?

Annuler la réponse

Annuler la réponse