La géométrie n’est pas ton dada ? Pas de panique, les Sherpas sont là pour t’aider ! Et pour cela, on t’a préparé une fiche de maths pour t’apprendre à calculer le volume d’une boule et l’aire d’une sphère ! Tu es prêt ? À ta calculette et c’est parti ! 🧮

Une sphère et une boule, quelle différence ? 👀
Définitions 📖
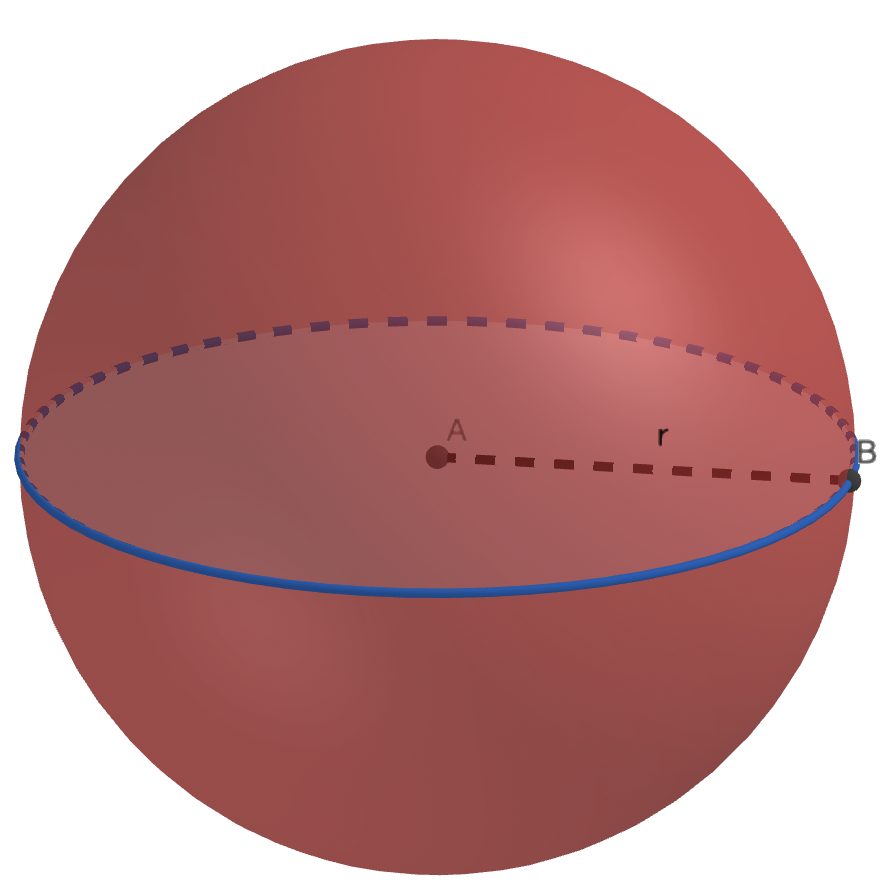
Définition d’une sphère
La sphère de centre A et de rayon r est représentée par l’ensemble des points situés à une même distance du centre appelée « rayon ». Par exemple, le point B est un de ces points. Elle correspond uniquement à la surface !
Définition d’une boule
La boule de centre A et de rayon r est représentée par l’ensemble des points qui sont situés à une distance inférieure ou égale au rayon par rapport au centre.
Voici leur différence ! La sphère est la surface extérieure, car elle est vide. La boule est l’espace intérieur d’une sphère, car elle est est remplie. Au final, une boule n’est rien d’autre qu’une sphère pleine.
Exemple
Un ballon de basket est une sphère alors que la Terre est une boule ! C’est pour cela que l’on calcule l’aire de la sphère et non son volume.

💡Le savais-tu ?
Le mot sphère vient du grec sphaira qui signifie balle à jouer. Tout s’explique ! 🤔

Ton premier cours particulier est offert ! 🎁
Nos profs sont passés par les meilleures écoles et universités.
Les notions à connaître 👩🏫
Avant de passer aux formules, tu dois connaître quelques notions !
Le rayon
Le rayon d’un cercle, d’une sphère ou d’une boule est un segment de droite qui relie le centre à son périmètre. Le rayon est la moitié du diamètre.
En image, ça donne ça 👇
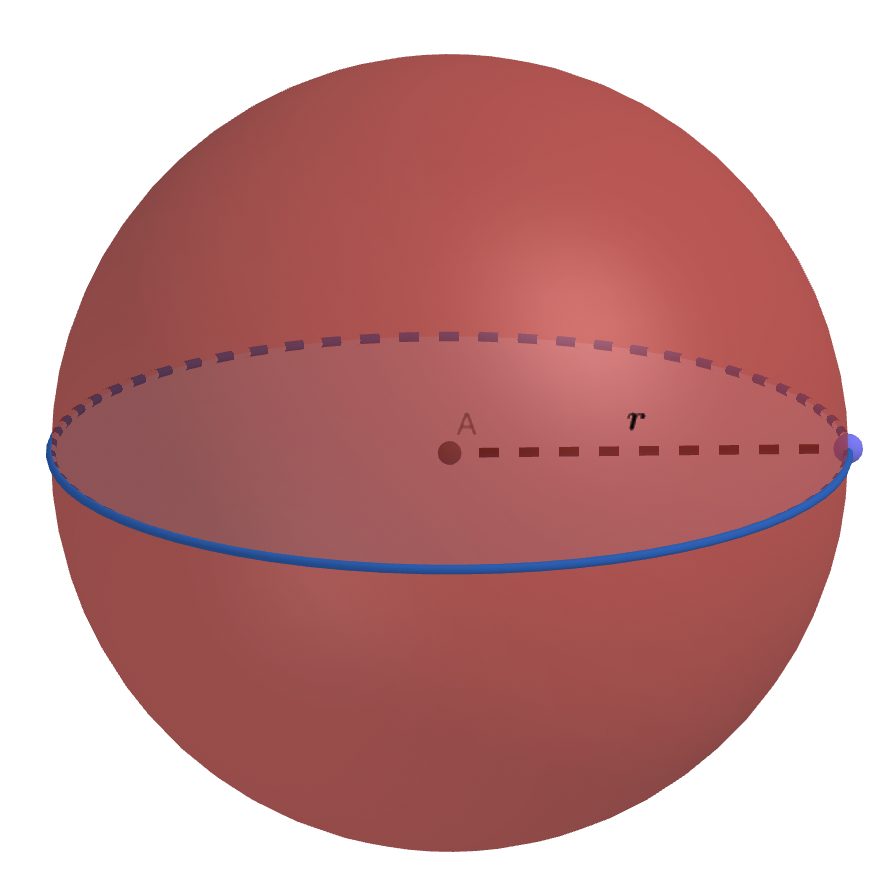
Le diamètre
Quant au diamètre d’un cercle, d’une sphère ou d’une boule, c’est est un segment de droite passant par le centre et qui joint deux points du périmètre.
En image, ça donne ça 👇
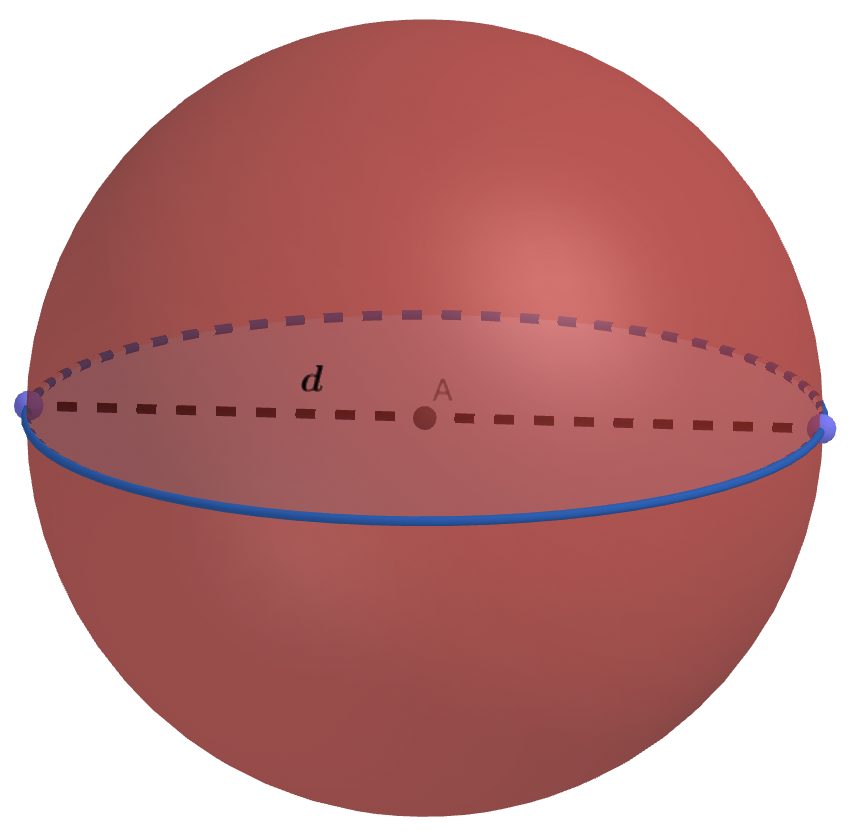
Le nombre pi
Le nombre (pi) est une constante mathématique qui représente la relation entre la circonférence d’un cercle et son diamètre. On l’utilise aussi pour la sphère et la boule !
La valeur de est un nombre irrationnel, ce qui signifie qu’il ne peut pas être exprimé de manière exacte comme une fraction, et qu’il a une expansion décimale infinie. Les premières décimales de π sont approximativement 3,14159265359, mais il n’y aucune possibilité de prévoir le chiffre d’après car il n’y a pas de suite logique.
💡 Le savais-tu ?
Il existe un moyen mnémotechnique pour retenir les 30 premières décimales de pi ! Il s’agit d’un poème d’un certain Maurice Decerf (on ne sait pas qui se cache derrière ce pseudonyme). Le code est que le nombre de lettres de chaque mot correspond à un chiffre.
Que j’aime à faire apprendre un nombre utile aux sages
3 1 4 1 5 9 2 6 5 3 5
Immortel Archimède, artiste ingénieur,
8 9 7 9
Qui de ton jugement peut priser la valeur ?
3 2 3 8 4 6 2 6
Pour moi, ton problème eut de pareils avantages.
4 3 3 8 3 2 7 9
➡️ 3,141592653589793238462643383279
À lire aussi
📐 Révise le tétraèdre grâce à notre fiche de cours !
Calcul de l’aire d’une sphère 🧮
Formule avec le rayon
La formule de l’aire d’une sphère est la suivante :
Formule avec le diamètre
Comme le rayon est deux fois le diamètre, la formule peut s’écrire aussi comme ça :
⚠️
L’aire s’exprime en cm2

Calcul du volume d’une boule 🧮
Formule avec le rayon
La formule du volume d’une boule est la suivante :
Formule avec le diamètre
Ici aussi, comme le rayon est deux fois le diamètre, la formule peut s’écrire aussi comme ça :
Démonstration
On sait que
On remplace r par dans la formule d’origine.
On a bien donc :
⚠️
Le volume s’exprime en cm3
À lire aussi
🧮 Apprends à calculer le volume d’un cylindre avec notre fiche de cours !
Besoin d’un prof particulier ? ✨
Nos profs sont là pour t’aider à progresser !
Exercices ✍️
Maintenant, c’est à toi de jouer ! On te donne quelques exercices de calcul à résoudre.

Exercice 1
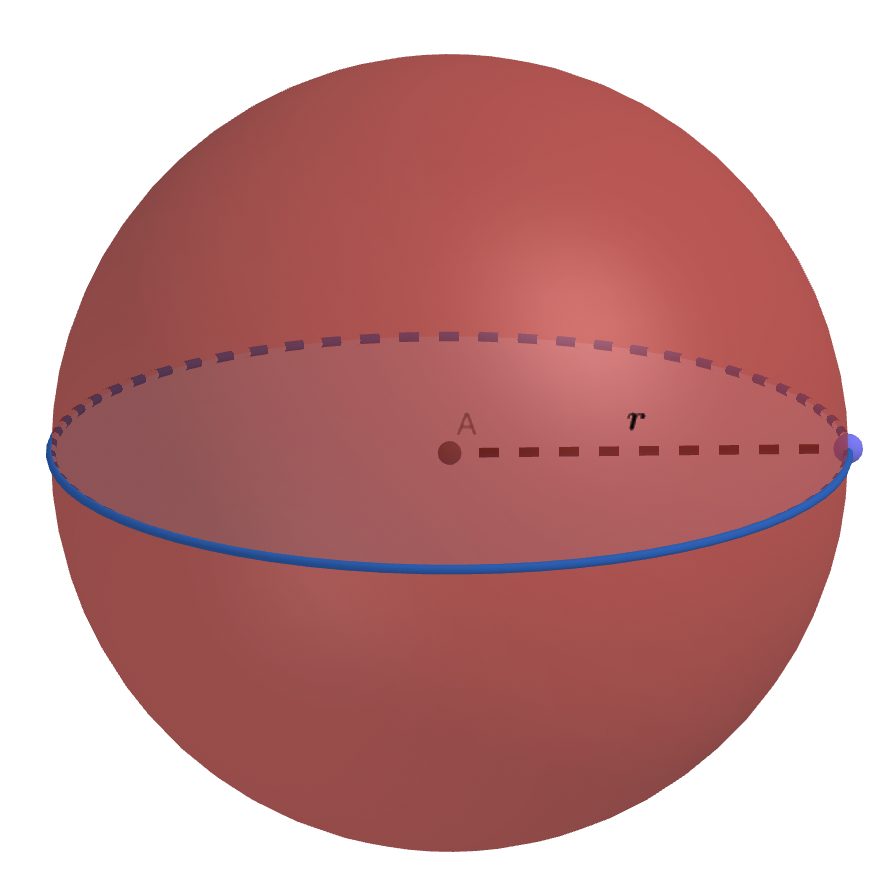
Soit une sphère de rayon r=7, quelle est son aire ?
Exercice 2
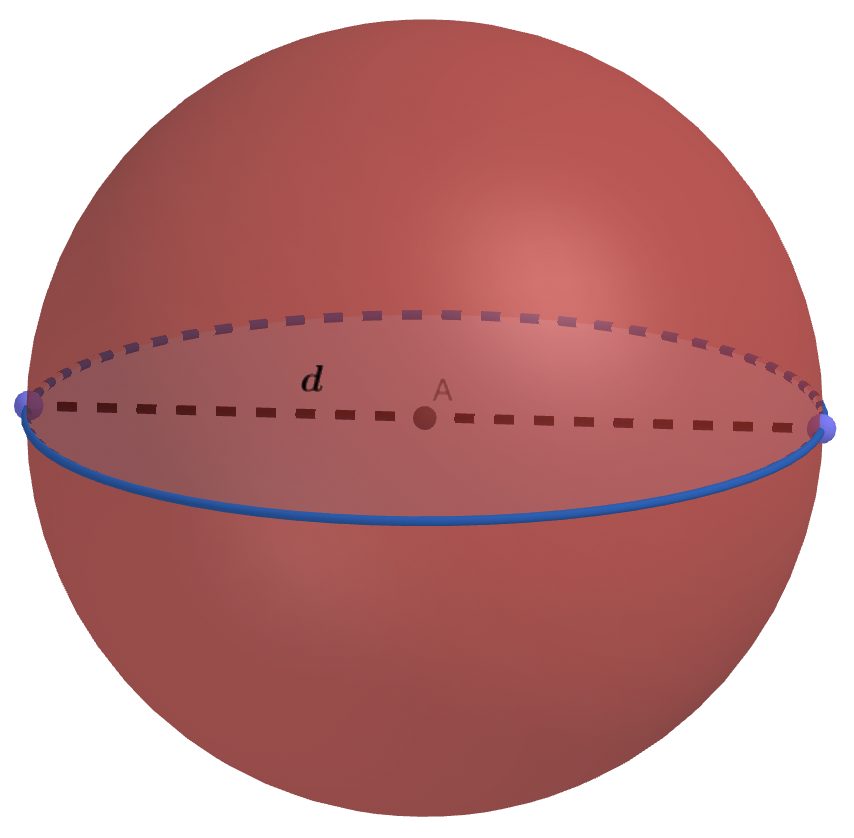
Soit une sphère de diamètre d=24, quelle est son aire ?
Exercice 3
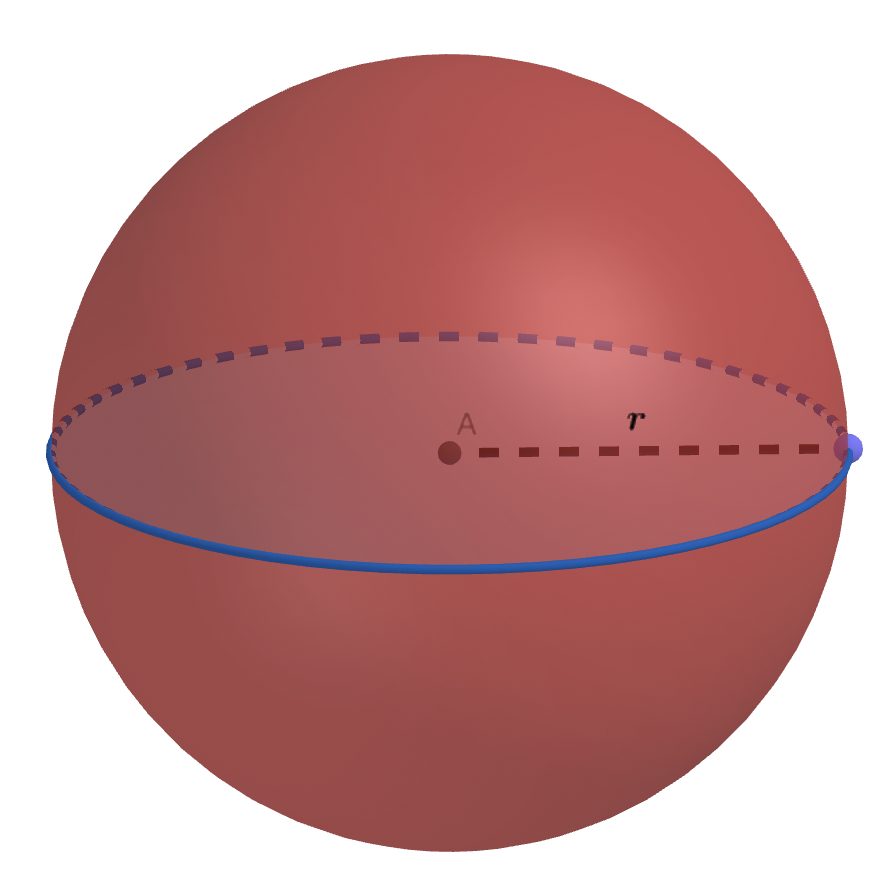
Soit une boule de rayon r=5, quel est son volume ?
Exercice 4
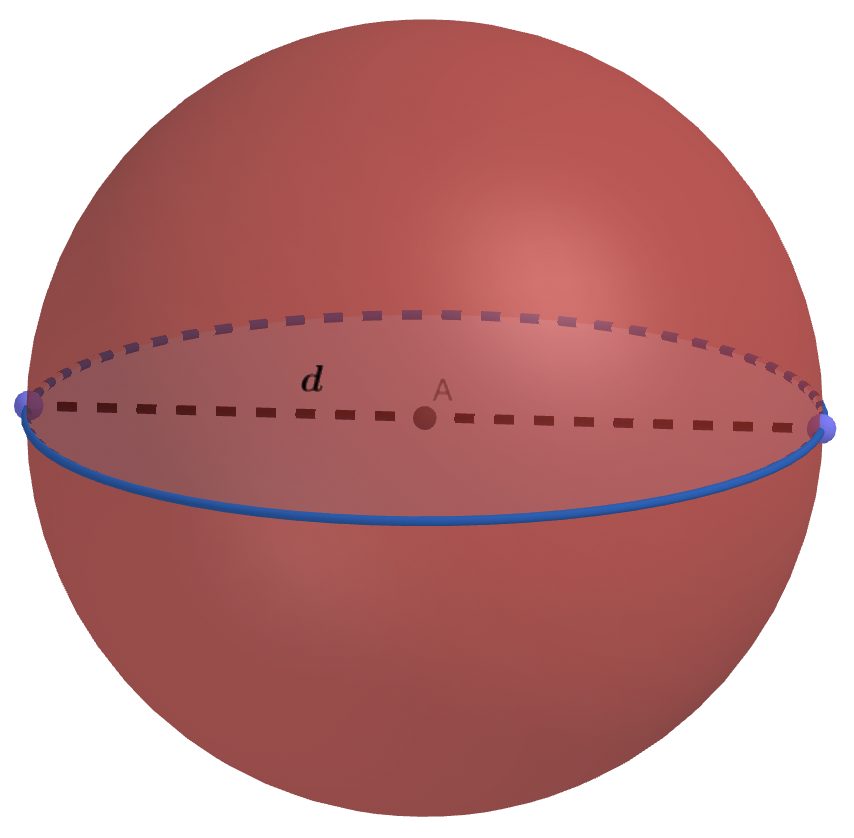
Corrigés 💯
Corrigé 1
On applique la formule :
Avec pi, vaut mieux prendre la calculatrice pour avoir le nombre le plus rapproché !
Corrigé 2
On applique la formule :
Corrigé 3
On applique la formule :
Corrigé 4
On applique la formule :
Si tu as des difficultés à résoudre ces exercices, n’hésite pas à prendre des cours particuliers de maths avec un de nos Sherpas !

Voilà, tu sais maintenant calculer le volume d’une boule et l’aire d’une sphère ! On espère que cette fiche de géométrie t’a aidé. N’hésite pas à parcourir notre blog pour réviser d’autres notions en mathématiques ! 🙌