🧠 9 moyens mnémotechniques pour réussir en maths

Sommaire

Un moyen mnémotechnique, c’est quoi ?
Moyens mnémotechniques en maths

Tu as du mal à te souvenir de formules, de règles ou de nombre en mathématiques ? Tu tombes bien alors ! On t’a préparé 9 moyens mnémotechniques pour réussir en maths. Pas besoin de calculatrice aujourd’hui, il te suffit d’apprendre par cœur les méthodes qu’on te donne. Tu es prêt ? C’est parti ! 🚀

Je ne m'en souviens pas di le monsieur — *Toi, avant de lire cet article !*

Un moyen mnémotechnique, c’est quoi ? 👀

Définition 📖

⚠️ On dit “mnémotechnique” et non “mémotechnique” !

Le mot mnémotechnique vient de la combinaison du mot mnêmê, qui signifie la mémoire, et technè qui signifie production en grec. On retrouve aussi la racine mnêmê dans le mot amnésie, quelqu’un qui a perdu la mémoire.

Selon le Larousse, mnémotechnique “se dit de procédés utilisés en vue de mieux fixer certains souvenirs, ou d’être plus aisément à même de les retrouver”.

Il doit sûrement exister autant de moyens mnémotechniques que de choses à retenir. Ils peuvent être sous forme d’images, d’acronymes, d’acrostiches, de rimes, de codes, etc.

💡 Idée

Quand tu as du mal à retenir une notion de cours, use de ton imagination et crée ton propre moyen mnémotechnique ! Par exemple, tu peux créer un code dont tu es le seul à pouvoir déchiffrer. Rien que le fait d’avoir cherché pendant un moment une méthode va t’aider à t’en souvenir toute ta vie.

Une femme fait des signes et un homme ne comprend rien. — *Quand tu es le seul à comprendre ton code !*

Louise

Mines ParisTech

24€/h

Antoine

Sciences Po Paris

18€/h/h

Emilie

Sciences Po Lyon

19€/h

Agathe

ENS Lyon

19€/h

Pierre

ESSEC

16€/h

Martin

HEC Paris

23€/h

Fanny

Ponts ParisTech

19€/h

Hugo

Insa Lyon

16€/h

Ton premier cours particulier est offert ! 🎁

Nos profs sont passés par les meilleures écoles et universités.

J’EN PROFITE MAINTENANT !

Quelques exemples ↪️

Pour t’aider à mieux comprendre, on te donne quelques exemples. Attention, tu risques sûrement de replonger dans tes souvenirs d’enfance.

👉 On ne peut pas parler de moyens mnémotechniques sans parler du bon vieux “Ornicar”, on le connaît tous celui-ci et on se demande depuis toujours où il se trouve ! “Mais où est donc Ornicar ?”, ce moyen mnémotechnique qui t’a aidé à te rappeler des conjonctions de coordination en français : mais, ou, et, donc, or, ni, car.

Un homme qui pleure avec un sourire nostalgique — *Toi, nostalgique de l’époque d’Ornicar…*

👉 En géographie pour savoir où placer l’ouest et l’est sur une carte, tu n’as qu’à penser au mot “OrangE”. Le O pour l’ouest à gauche et le E pour l’est à droite.

👉 Si tu es un féru d’astronomie, retiens l’ordre des planètes grâce à cette phrase : “Mélanie, vous tombez mal, je suis un navet”.

Mercure, Vénus, Terre, Mars, Jupiter, Saturne, Uranus, NeptuneChaque première lettre représente une planète. Mercure et Mars commencent toutes les deux par la même lettre ? Pas de souci, pour ces deux planètes, tu prends les deux premières lettres : “Mélanie” pour “Mercure” et “Mal” pour “Mars”.

💡 Le savais-tu ?

Pluton, découverte en 1930, a longtemps été considérée comme la 9^e planète du système solaire. Mais depuis 2006, Elle n’a plus le statut de planète, mais celui d’une “planète naine”. En fait, dans les années 2000, trois planètes de la même taille que Pluton ont été découvertes. Les astronomes ont donc compris qu’il y en avait d’autres et ont décidé de la rétrograder !

D’ailleurs, avant 2006, on pouvait rajouter “pourri” à la fin de la phrase mnémotechnique pour “Pluton” !

Un homme qui dit que c'est trop petit. — *Quand on a annoncé à Pluton qu’elle ne faisait plus partie des planètes du système solaire…*

À quoi ça sert ? 🤔

Mais alors, pourquoi apprendre un mot, une phrase ou un poème si tu peux juste apprendre par cœur la notion à connaître ? On t’explique !

Un moyen mnémotechnique est un outil puissant pour améliorer ta mémorisation. Ton cerveau a besoin d’être stimulé pour retenir des informations et un moyen mnémotechnique est une bonne méthode pour y arriver.

Associer une image, un mot, un code, etc., à une information complexe à connaître, va te la faire mémoriser beaucoup plus aisément. On se rappelle plus facilement des informations simples que des informations compliquées, n’est-ce pas ?

ça a l'air facile de s'en souvenir dit Bob l'éponge

⚠️ Pas pour n’importe quelle information !

Les moyens mnémotechniques sont plus efficaces pour certains types d’information que pour d’autres.

Ils sont très utiles pour retenir des éléments isolés comme des formules, des listes, une suite de chiffres, des dates, etc.

Cependant, en ce qui concerne les concepts complexes à connaître et comprendre, ils sont moins utiles.

Clémence

HEC Paris

21€/h/h

Thibault

ENS Paris Ulm

20€/h

Sophie

Sciences Po Bordeaux

12€/h

Noémie

M2 en droit à Assas

19€/h

Fanny

Ponts ParisTech

19€/h

Simon

4e année de médecine

26€/h

Nicolas

CentraleSupélec

17€/h

Victor

ESCP

25€/h

Besoin d’un prof particulier ? ✨

Nos profs sont là pour t’aider à progresser !

JE PRENDS UN COURS GRATUIT !

Moyens mnémotechniques en maths 💡

1. Pour te souvenir de l’ordre des opérations

Pour retenir l’ordre de priorité des opérations, un moyen bien connu est le mot : PEMDAS.

Oui, on te l’accorde, ça ne veut rien dire, mais il est facile à mémoriser.

PEMDAS : parenthèse, exposant, multiplication, division, addition, soustraction.

Une femme qui ne sait pas par où commencer. — *Ce ne sera plus le cas avec la méthode PEMDAS !*

Retiens donc qu’il faut commencer par les parenthèses, puis les exposants (appelés aussi “puissances”), les multiplications et/ou les divisions, et enfin, on termine par les additions et/ou les soustractions.

Utile quand tu te retrouves face à une opération comme ça :

$5+3\times(6+9)-6^2+\sqrt{4}-\frac{49}{7}$

👉 P : on commence par la parenthèse $(6+9)=15$
$5+3\times15-6^2+\sqrt{4}-\frac{49}{7}$

👉 E : les exposants $6^2=36$ et $\sqrt{4}=2$
$5+3\times15-36+2-\frac{49}{7}$

👉 M : la multiplication $3\times15=45$
$5+45-36+2-\frac{49}{7}$

👉 D : la division $\frac{49}{7}=7$
$5+45-36+2-7$

👉 A : les additions $5+45=50$ et $36+2=38$
$50-38-7$

👉 S : les soustractions $50-38-7=-5$
$-5$

➡️ $5+3\times(6+9)-6^2+\sqrt{4}-\frac{49}{7}=-5$

💡 Rappel exposant et racine

La racine carrée d’un nombre “a” est le nombre “a” à la puissance ½ : √a=a^1/2
Donc, la racine est un exposant.

2. Pour vérifier que tu as bien appliqué la double distributivité

Le mot “PIED” aide à vérifier que tu as bien tous les éléments d’un développement en utilisant la double distributivité.

P : premiers

I : intérieurs

E : extérieurs

D : derniers

(a+b)(c+d) = ac + ad + bc + bd

👉 Premiers : ac

👉 Intérieurs : bc

👉 Extérieurs : ad

👉 Derniers : bd

Un homme qui fait le signe du check. — *Quand tu vérifies que tu as bien tous les éléments de ton développement !*

💡 Le savais-tu ?

Le moyen mnémotechnique équivalent pour les Anglo-saxons est bien plus connu chez eux. Il s’agit de la FOIL method!

(a+b)(c+d) = ac + ad + bc + bd
F : first → premier → ac
O : outside → extérieur → ad
I : inside → intérieur → bc
L : last → dernier → bd

Il est sûrement plus répandu parce qu’il permet non seulement de vérifier qu’on a tous les éléments, mais aussi d’appliquer l’ordre de distributivité.

Tu peux utiliser celui-ci si c’est plus simple pour toi !

3. Pour repérer le numérateur et le dénominateur

Pour te souvenir de la place du numérateur et de celle du dénominateur dans une fraction, pense à ces images :

un nuage pour le numérateur,
et un démon pour le dénominateur.

Le nuage est en haut dans le ciel et le démon en bas en enfer.

☁️

$\frac{Numérateur}{Dénominateur}$

👿

Peach en enfer souhaitant la bienvenue. — *Quand tu dois réduire au même dénominateur !*

4. Pour retenir des formules en géométrie

Pour retenir les formules du périmètre d’un cercle, de l’air d’un disque et du volume d’une sphère, on te donne un joli poème !

Le cercle est fier
D’être égal à deux pierres

$2\times\pi\times{R}$

Le disque est tout heureux
D’être égal à pierre deux

$\pi\times{R}^2$

Le volume de la sphère
Qu’elle soit de pierre
Ou bien de bois
Est égal à quatre tiers de pierre trois

$\frac{4}{3}\times\pi\times{R}^3$

💡 Formules

Périmètre cercle = 2.π.R
Air disque = π.R²
Volume sphère = 4/3.π.R³

Avec R le rayon.

5. Pour retenir les 30 premières décimales de pi

En parlant de pi ( $\pi$ ), sais-tu que tu peux retenir ses 30 premières décimales facilement grâce à un poème. Le code est que le nombre de lettres de chaque mot correspond à un chiffre.

En parlant de pi, sais-tu que tu peux retenir ses 30 premières décimales facilement grâce à un poème ? Le code est que le nombre de lettres de chaque mot correspond à un chiffre.

Que j’aime à faire apprendre un nombre utile aux sages

3 1 4 1 5 9 2 6 5 3 5

Immortel Archimède, artiste ingénieur,

8 9 7 9

Qui de ton jugement peut priser la valeur ?

3 2 3 8 4 6 2 6

Pour moi, ton problème eut de pareils avantages.

4 3 3 8 3 2 7 9

➡️ 3,141592653589793238462643383279

🤔 Le nombre pi, à quoi ça sert ?

Le nombre pi, aussi appelé constante d’Archimède, noté π, est le rapport constant de la circonférence d’un cercle à son diamètre dans un plan euclidien. On peut également le définir comme le rapport de l’aire d’un disque au carré de son rayon. C’est pour cela qu’on l’utilise en géométrie.

Pour les plus aguerris, une version plus longue permet de connaître les 100 premières décimales de pi ! (Quand le nombre de lettres est de 10, il s’agit d’un 0.)

Que j’aime à faire apprendre ce nombre utile aux sages !

3 1 4 1 5 9 2 6 5 3 5

Immortel Archimède, artiste ingénieur,

8 9 7 9

Qui de ton jugement peut priser la valeur ?

3 2 3 8 4 6 2 6

Pour moi, ton problème eut de pareils avantages.

4 3 3 8 3 2 7 9

Jadis, mystérieux, un problème bloquait

5 0 2 8 8

Tout l’admirable procédé, l’œuvre grandiose

4 1 9 7 1 6 9

Que Pythagore découvrit aux anciens Grecs.

3 9 9 3 7 5

0 quadrature ! Vieux tourment du philosophe

1 0 5 8 2 9

Insoluble rondeur, trop longtemps vous avez

9 7 4 9 4 4

Défié Pythagore et ses imitateurs.

5 9 2 3 0

Comment intégrer l’espace plan circulaire ?

7 8 1 6 4 0

Former un triangle auquel il équivaudra ?

6 2 8 6 2 0

Nouvelle invention : Archimède inscrira

8 9 9 8

Dedans un hexagone ; appréciera son aire

6 2 8 0 3 4

Fonction du rayon. Pas trop ne s’y tiendra :

8 2 5 3 4 2 1 1 7

Dédoublera chaque élément antérieur ;

0 6 7 9

Toujours de l’orbe calculée approchera ;

8 2 1 4 8 0

Définira limite ; enfin, l’arc, le limiteur

8 6 5 1 3 2 8

De cet inquiétant cercle, ennemi trop rebelle

2 3 0 6 6 4 7

Professeur, enseignez son problème avec zèle

0 9 3 8 4 4

Si savoir autant de décimales du nombre pi ne t’est pas vraiment nécessaire pour tes cours, tu peux toujours te servir de cette information pour briller en société !

Martin

HEC Paris

23€/h

Jade

Sciences Po Paris

21€/h

Bastien

Polytechnique

26€/h

Emilie

Sciences Po Lyon

19€/h

Hugo

Insa Lyon

16€/h

Alma

ENS Paris-Saclay

24€/h

David

EDHEC

25€/h

Jeanne

Aix-Marseille Université

17€/h

Besoin de cours particuliers ? ✨

4 points de plus sur ta moyenne avec nos profs Sherpas ! 📈

JE PRENDS UN COURS GRATUIT !

6. Pour te souvenir des formules trigonométriques

Pour retenir les formules du sinus, du cosinus et de la tangente en trigonométrie, tu n’as qu’à retenir “SOH CAH TOA” !

👉 SOH : Sinus = Opposé/Hypoténuse

👉 CAH : Cosinus = Adjacent/Hypoténuse

👉 TOA : Tangente = Opposé/Adjacent

💡Rappel

La trigonométrie s’applique aux triangles rectangles et fait un lien entre les angles et les côtés.
Cela te permet de :

déduire la longueur de deux côtés quand tu connais la longueur d’un côté et la mesure d’un angle,
calculer la mesure des angles quand tu connais la longueur de deux côtés.

Soit un triangle rectangle en A, voici comment on détermine le côté opposé et le côté adjacent d’un angle.

Sachant que l’hypoténuse est toujours la même, c’est-à-dire le côté le plus long en face de l’angle droit, le côté opposé à l’angle B est à en face (à l’opposé) et son côté adjacent est à côté de lui. Pour l’angle C, c’est la même chose ! Son côté opposé est en face et son adjacent à côté.

↪️ Exemple :

Admettons que dans notre schéma précédent :

g = 6 cm,
f = 8 cm,
h = 10 cm.

À combien est égal le sinus de l’angle B ?

Dans le groupe de mots “SOH CAH TOA”, on va s’intéresser au mot “SOH”

sin = côté opposé/hypoténuse = 6/10 = 0,6

Le sinus de l’angle B est égal à 0,6

7. Pour retenir le nombre d’or

Pour retenir le nombre d’or, tu n’as qu’à mémoriser cette phrase :

“Ô nombre d’élégance ! Toi, toi, grandiose, étonnant”

1 6 1 8 0 3 3 9 8

C’est encore un code. Le nombre de lettres de chaque mot correspond à un chiffre (le point d’exclamation “!” représente le zéro)

Le nombre d’or est égal à environ 1,61803398.

Le nombre d’or, aussi appelé proportion divine, souvent désigné par la lettre grecque $\phi$ , est une proportion définie comme le seul rapport $\frac{a}{b}$ entre deux longueurs a et b. Le rapport de la somme a + b des deux longueurs sur la plus grande (a) est égal à celui de la plus grande (a) sur la plus petite (b) : $\frac{a+b}{a}=\frac{a}{b}$

C’est la formule de l’harmonie.

On l’utilise dans les domaines des mathématiques, de l’architecture, du design, de l’art, de la photographie, etc.

🖼️ Le savais-tu ?

Léonard de Vinci est l’artiste qui a introduit les mathématiques dans l’art avec le nombre d’or. D’abord en réalisant l’Homme de Vitruve, dit l’Homme parfait puis avec La Joconde, l’un des tableaux les plus célèbres du monde.

La Joconde disant qu'elle n'est pas tout le monde, qu'elle est la Joconde dans un talkie walkie. — *Quand tu as des proportions divines !*

8. Pour te souvenir de l’ordre des unités de grandeur

Tu te perds dans l’ordre des unités de grandeur ? Pas de panique. Tu n’as qu’à apprendre cette phrase :

“King Henry Died Unexpectedly Drinking Chocolate Milk” (On ne se méfie jamais assez du chocolat au lait 😅).

Kilomètre, Hectomètre, Décamètre, Unité de base (mètre), Décimètre, Centimètre, Millimètre.

Et ça marche avec les autres unités de mesure. Tu n’as qu’à modifier le “mètre” en “gramme” par exemple. Kilogramme, Hectogramme, Décagramme, Unité de base (gramme), Décigramme, Centigramme, Milligramme.

9. Pour différencier l’axe des abscisses de l’axe des ordonnées

Tu hésites au moment où il faut placer un point sur l’axe des abscisses et des ordonnées. T’inquiète pas ! On a plusieurs moyens mnémotechniques pour toi.

Le premier moyen mnémotechnique visuel est l’image du jeu de la pyramide pour les enfants.

Quand un enfant met les cercles dans le bâton vertical, le jeu s’ordonne. L’axe des ordonnées est donc vertical et celui des abscisses horizontal !

Un second moyen mnémotechnique est de te dire que la flèche monte vers le haut, en phonétique ça donne “O” comme “ordonnée”.

Un troisième et dernier moyen mnémotechnique qu’on peut te donner est de dessiner ceci sur ton brouillon :

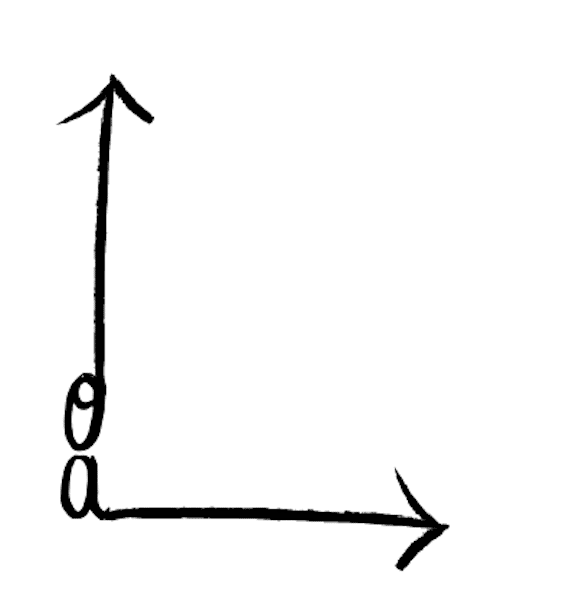
La queue du “a” de “abscisses” est à l’horizontale et la boucle du “o” de “ordonnées” est à la verticale.

Avec tous ces moyens mnémotechniques, tu ne risques plus de confondre l’axe des abscisses avec celle des ordonnées !

3 personnes réunies autour d'un cube disent qu'il y a trop de possibilités.

Voilà, notre article sur les moyens mnémotechniques en mathématiques touche à sa fin. On espère que tu en as découvert beaucoup qui t’aideront dans tes études !

Une femme dit que la mémorisation, c'est son truc, en buvant du café. — *Toi, maintenant que tu as lu cet article !*

D’ailleurs, toi aussi, partage avec nous tes meilleurs moyens mnémotechniques en commentaires. Et si tu as des difficultés, n’hésite pas à prendre contact avec un de nos professeurs de maths en ligne !

4/5 - (23 votes)

Sommaire

Un moyen mnémotechnique, c’est quoi ?
Moyens mnémotechniques en maths

Annuler la réponse

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉

Traore dit :

18 janvier 2025 à 15h32

Extraordinaire

Répondre
1. La Rédac des Sherpas dit :
  
  24 janvier 2025 à 11h42
  
  Bonjour,
  
  Merci pour ton commentaire ! 🌟
  
  À très bientôt !
  
  Répondre

9 moyens mnémotechniques pour réussir en maths 🧠

Un moyen mnémotechnique, c’est quoi ? 👀

Définition 📖

Quelques exemples ↪️

À quoi ça sert ? 🤔

Moyens mnémotechniques en maths 💡

1. Pour te souvenir de l’ordre des opérations

2. Pour vérifier que tu as bien appliqué la double distributivité

3. Pour repérer le numérateur et le dénominateur

4. Pour retenir des formules en géométrie

5. Pour retenir les 30 premières décimales de pi

6. Pour te souvenir des formules trigonométriques

7. Pour retenir le nombre d’or

8. Pour te souvenir de l’ordre des unités de grandeur

9. Pour différencier l’axe des abscisses de l’axe des ordonnées

Annuler la réponse

Annuler la réponse