Le Tétraèdre {fiche de Géométrie} 🔺

Sommaire

Qu’est-ce qu’un tétraèdre ?
Le tétraèdre régulier
Les formules à connaître
Exercices pratiques

Aaaah la géométrie, cette matière terrifiante, mais utile dans énormément de domaines comme l’architecture, la construction, l’aéronautique ou encore l’astronomie. Aujourd’hui, on va te parler d’un des solides phares de la géométrie : la pyramide et encore plus précisément, le tétraèdre !

Alors si tu as comme projet de reconstruire les pyramides d’Égypte (ou plus simplement de réussir ton contrôle de maths 😅), tu es au bon endroit !

Qu’est-ce qu’un tétraèdre ?

Définition

Pour définir un tétraèdre, il faut d’abord bien comprendre ce qu’est une pyramide 👇

Une pyramide est un solide caractérisé par deux choses :

📌 Une face polygonale (qui a plusieurs angles et plusieurs côtés) qu’on nomme “base”.

📌 Les autres faces sont, elles, triangulaires, et se rejoignent en un point nommé “sommet”.

Maintenant, on peut revenir à notre tétraèdre : il s’agit donc d’une pyramide, mais avec la particularité d’avoir comme base un triangle ! Toutes les faces de ce solide sont donc triangulaires, contrairement à des pyramides qui peuvent avoir comme base un carré, un rectangle, un losange, etc.

Caractéristiques

👉 4 faces triangulaires

👉 6 arêtes

👉 4 sommets

💡 Le savais-tu ?

“Tétra” signifie “quatre” en latin et “edre” vient du mot “edra” en grec ancien qui signifie “face” ! Petit moyen mnémotechnique, pour retenir que dans un tétraèdre il y a forcément quatre faces 😉

Le tétraèdre régulier

Un tétraèdre régulier est un tétraèdre possédant quatre faces identiques, c’est-à-dire quatre triangles isocèles et égaux.

De ce fait, on en déduit des caractéristiques spécifiques sur les angles de celui-ci 👇

👉 Les faces adjacentes forment obligatoirement des angles de 60 degrés

👉 Deux arêtes avec une extrémité en commun forment aussi un angle de 60 degrés

Pratique pour la trigonométrie !

Les formules à connaître

Le calcul de l’aire et du volume d’un tétraèdre va surtout dépendre de s’il est régulier ou non. Pas de panique, on te montre plusieurs formules selon les différentes situations 👇

Comment calculer l’aire d’un tétraèdre

Tétraèdre classique

Le tétraèdre étant un solide avec plusieurs faces triangulaires, il te suffit de calculer l’aire de chacune de ses faces triangulaires et de les additionner ensuite 👇

💡 Rappel : Calculer l’aire d’un triangle

📌 Pour calculer l’aire d’un triangle, la formule est : (base x hauteur) / 2

📌 Une aire est toujours exprimée en cm carré

On a par exemple un triangle ABC avec :

$Hauteur AB = 6 cm$

$Base BC = 5 cm$

L’aire du triangle ABC est donc égale à

$\frac{5\times6}{2}=15 cm^2$

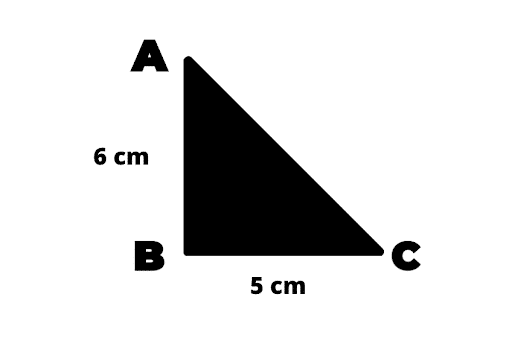
La hauteur est relative au côté que tu choisis comme base. Si on avait choisi AB comme base, sa hauteur relative aurait donc été BC.

💡 Pour info

La hauteur est le segment perpendiculaire à la base reliant un sommet. Dans le cas d’un triangle rectangle en B, la hauteur peut être BC ou AB selon la base que tu choisis 😉

👉 Maintenant que tu sais calculer l’aire d’un triangle, il nous suffit d’additionner l’aire de chacun des triangles composant un tétraèdre.

Calculons l’aire du tétraèdre quelconque ABCD à l’aide de son patron.👇

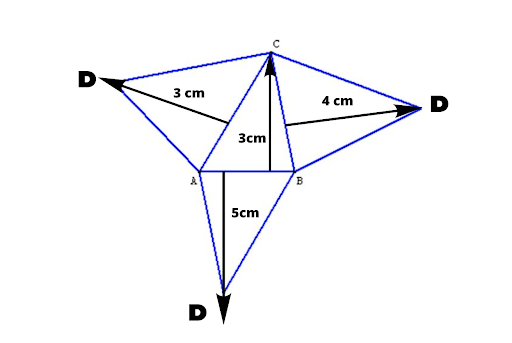
On a :

$Hauteur ABD = 5 cm$

$Hauteur ACD = 3 cm$

$Hauteur CBD = 4 cm$

$Hauteur ABC = 3 cm$

$AB = 2 cm$

$CB = 3 cm$

$AC = 5 cm$

Alors :

$Aire ABD = \frac{2\times5}{2}=5 cm^2$

$Aire ACD = \frac{5\times3}{2}=7,5 cm^2$

$Aire CBD = \frac{3\times4}{2}=6 cm^2$

$Aire ABC = \frac{2\times3}{2}=3 cm^2$

Finalement, l’aire du tétraèdre ABCD est donc égale à :

$=Aire ABD+AireACD+AireCBD+AireABC$

$=5 + 7,5 + 6 + 3$

$=21,5 cm^2$

Tétraèdre régulier

👉 Dans le cas d’un tétraèdre régulier, toutes les faces sont des triangles équilatéraux. Il suffit donc de calculer l’aire d’un seul triangle et de le multiplier par 4 !

Calculons l’aire du tétraèdre régulier ABCD avec chaque côté (arête) égal à 8 cm et une hauteur de 6,93 cm.👇

On a :

$Aire ABC=\frac{6,93\times8}{2}=27,7 cm^2$

On a donc :

$Aire ABCD={Aire ABC\times4}$

$Aire ABCD={27,7\times4}$

$Aire ABCD=110.9 cm^2$

Et si je te disais qu’il existe une formule beaucoup plus simple dans le cas d’un tétraèdre régulier 😅.

Eh oui, sinon il te suffit d’utiliser la formule suivante :👇

$Aire ABCD=\sqrt{3}\times{a^2}$ $avec$ $a$ $la$ $longueur$ $d'un$ $côté$ $(arête)$

$Aire ABCD=\sqrt{3}\times{8^2}$

$Aire ABCD=110.9 cm^2$

💡 Pour info

Cette formule te permet d’être beaucoup plus précis et surtout de ne pas avoir besoin de la hauteur !

Comment calculer le volume d’un tétraèdre

Tétraèdre classique

👉 Le tétraèdre étant une pyramide, le calcul de son volume est similaire à celui des autres pyramides !

💡 Rappel : Calculer le volume d’une pyramide

📌 Pour calculer le volume d’une pyramide, la formule est : (Aire base x hauteur de la pyramide) / 3

📌 Un volume est toujours exprimé en cm cube

Calculons le volume du tétraèdre ABCS 👇

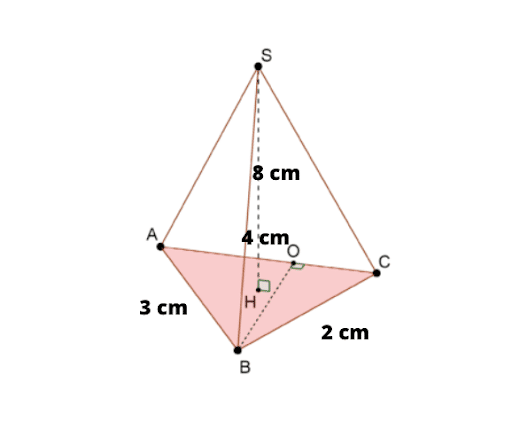
Calculons l’aire de la base ABC :

Hauteur BO = 2,90 cm

$Aire ABC =\frac{4\times2,90}{2}=5,8^2$

Calculons le volume ABCS :

Hauteur HS = 8

$Volume ABCS =\frac{5,8\times8}{3}=15,5^3$

💡 Pour info

La hauteur d’une pyramide est le segment reliant le centre de la base au sommet de la pyramide (dans ce cas, c’est HS).

Tétraèdre régulier

👉 Comme pour celui de l’aire, le calcul du volume d’un tétraèdre régulier est bien plus simple. Il suffit de connaître la longueur d’un des côtés (arêtes).

La formule est la suivante : 👇

$Volume=\frac{sqrt{2}}{12}}\times{a^3}$

Calculons le volume du tétraèdre régulier ABCD 👇

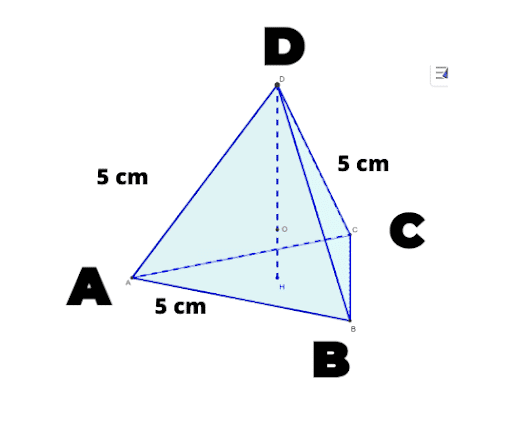
On a :

$a = 5cm$

Donc :

$Volume ABCD=\frac{sqrt{2}}{12}}\times{5^3}$

$Volume ABCD= 14,73 cm^3$

Récap des formules :

On te fait un petit récap des formules que tu viens de voir 👇

Calcul de l’aire :

📌 Triangle :

$\frac{base\times{hauteur}}{2}$

📌 Tétraèdre :

$La$ $Somme$ $de$ $l'aire$ $des$ $4$ $faces$

📌 Tétraèdre régulier :

$\{Aire d'une face}\times{4}$

$\sqrt{3}\times{a^2}$ $avec$ $a$ $la$ $longueur$ $d'un$ $côté$ $(arête)$

Calcul du volume :

📌 Tétraèdre classique ou pyramide :

$\frac{{aire de la base}\times{hauteur de la pyramide}}{3}$

📌 Tétraèdre régulier :

$Volume=\frac{sqrt{2}}{12}}\times{a^3}$ $avec$ $a$ $la$ $longueur$ $d'un$ $côté$ $(arête)$

$\frac{{aire de la base}\times{hauteur de la pyramide}}{3}$

Exercices pratiques

Calcul de l’aire d’un triangle

Exercice 1 : Détermine l’aire du triangle ABC, rectangle en B !

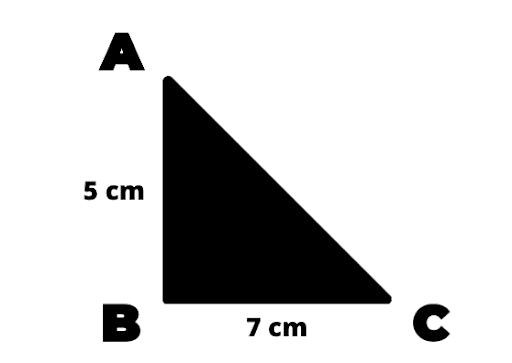
Correction :

👉 On a un triangle ABC rectangle en B :

$Hauteur AB = 5 cm$

$Base BC = 7 cm$

👉 L’aire du triangle ABC est donc égale à :

$\frac{AB\times{BC}}{2}$ $=\frac{5\times7}{2}=17,5 cm^2$

Exercice 2 : Détermine l’aire de ce triangle isocèle en B

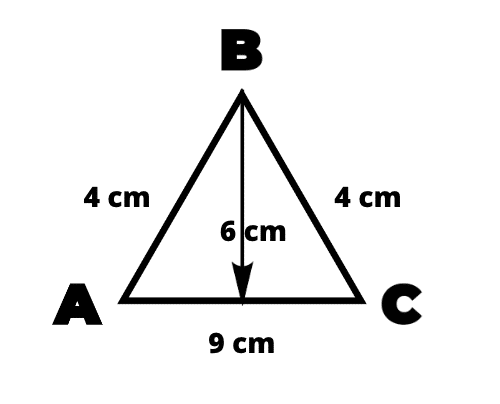
Correction :

👉 On a un triangle ABC isocèle en B :

$Hauteur AB = 6 cm$

$Base BC = 9 cm$

👉 L’aire du triangle ABC est donc égale à :

$\frac{AB\times{BC}}{2}$ $=\frac{6\times9}{2}= 27 cm^2$

Calcul de l’aire d’un tétraèdre

Exercice 1 : Détermine l’aire de ce tétraèdre ABCD

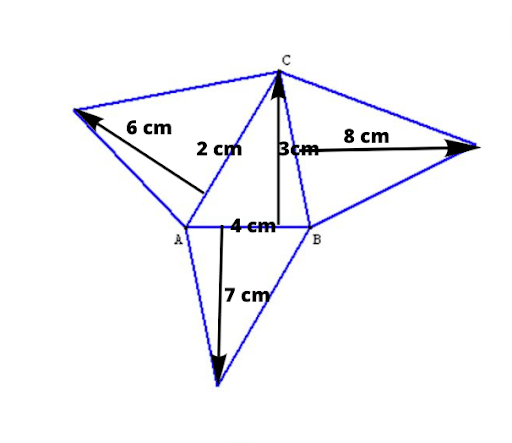
Correction :

👉 On a un tétraèdre ABCD

$Hauteur ABD = 7 cm$

$Hauteur ACD = 6 cm$

$Hauteur CBD = 8 cm$

$Hauteur ABC = 3 cm$

$AB = 4 cm$

$CB = 3 cm$

$AC = 22 cm$

👉 Calculons l’aire de chacune des faces :

$Aire ABD = \frac{2\times5}{2}=14 cm^2$

$Aire ACD = \frac{5\times3}{2}=6 cm^2$

$Aire CBD = \frac{3\times4}{2}=12 cm^2$

$Aire ABC = \frac{2\times3}{2}=6 cm^2$

👉 L’’aire du tétraèdre ABCD est donc égale à :

$=Aire ABD+AireACD+AireCBD+AireABC$

$=14 + 6 + 12 + 6$

$=38 cm^2$

Exercice 2 : Détermine l’aire de ce tétraèdre régulier ABCD

Correction :

👉 On a un tétraèdre régulier ABCD

$Hauteur$ $de$ $la$ $base$ $ABC$ $= 5,20 cm$

$Hauteur ACD = 6 cm$

👉 Calculons l’aire ABC :

$Aire ABC = \frac{6\times5,2}{2}=15,6 cm^2$

👉 L’aire ABCD est donc égale à :

$Aire ABCD=15,6\times{4}=62cm^2$

👉 On peut aussi utiliser la formule plus simple :

$Aire ABCD=\sqrt{3}\times{6^2}$

$Aire ABCD=62 cm^2$

Calcul du volume d’un tétraèdre

Exercice 1 : Détermine le volume de ce tétraèdre ABCS

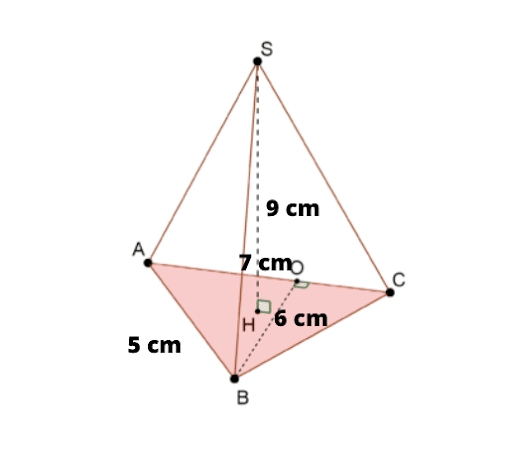
Correction :

👉 On a un tétraèdre ABCS

$Hauteur$ $de$ $la$ $base$ $ABC$ $= 6 cm$

$Hauteur$ $du$ $tétraèdre$ $ABCS$ $= 9 cm$

$AC = 7 cm$

👉 Calculons l’aire ABC

$Aire ABC = \frac{7\times6}{2}=21 cm^2$

👉 Le volume ABCS est donc égal à :

$Volume ABCS =\frac{21\times9}{3}=62cm^3$

Exercice 2 : Détermine le volume de ce tétraèdre régulier ABCD

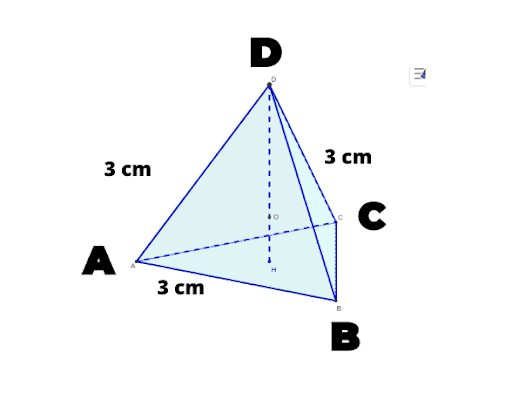
Correction :

👉 On a un tétraèdre régulier ABCD

$a = 3cm$

👉 Le volume du tétraèdre ABCD est donc égal à :

$Volume ABCD=\frac{sqrt{2}}{12}}\times{3^3}$

$Volume ABCD= 3,2 cm^3$

Voilà, maintenant, tu sais tout le tétraèdre et ses formules ! Retrouve nos autres fiches de cours de maths et n’hésite pas à contacter un Sherpas si tu as besoin d’aide ou que tu souhaites juste te perfectionner en maths !

4/5 - (8 votes)

Sommaire

Qu’est-ce qu’un tétraèdre ?
Le tétraèdre régulier
Les formules à connaître
Exercices pratiques

Annuler la réponse

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉

Tanji dit :

17 novembre 2024 à 23h35

Bonsoir,
Peut on calculer le volume d’un tetraedre à partir des soordonnées (sommets) ?
merci

Répondre
1. La Rédac des Sherpas dit :
  
  22 novembre 2024 à 14h15
  
  Oui, il est possible de calculer le volume d’un tétraèdre à partir des coordonnées de ses sommets. Voici comment :
  
  Identifiez les coordonnées des sommets du tétraèdre : A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3), D(x4, y4, z4).
  Calculez trois vecteurs formés par les arêtes issues du sommet A :
  AB = (x2 – x1, y2 – y1, z2 – z1)
  AC = (x3 – x1, y3 – y1, z3 – z1)
  AD = (x4 – x1, y4 – y1, z4 – z1)
  Utilisez ces vecteurs pour calculer un déterminant, qui représente un volume signé :
  V = (1/6) × valeur absolue du déterminant de la matrice formée par les coordonnées des vecteurs AB, AC et AD.
  
  Répondre

Géométrie : le tétraèdre, définition et formules 🔺

Qu’est-ce qu’un tétraèdre ?

Définition

Le tétraèdre régulier

Les formules à connaître

Comment calculer l’aire d’un tétraèdre

Tétraèdre classique

Tétraèdre régulier

Comment calculer le volume d’un tétraèdre

Tétraèdre classique

Tétraèdre régulier

Récap des formules :

Calcul de l’aire :

Calcul du volume :

Exercices pratiques

Calcul de l’aire d’un triangle

Exercice 1 : Détermine l’aire du triangle ABC, rectangle en B !

Exercice 2 : Détermine l’aire de ce triangle isocèle en B

Calcul de l’aire d’un tétraèdre

Exercice 1 : Détermine l’aire de ce tétraèdre ABCD

Exercice 2 : Détermine l’aire de ce tétraèdre régulier ABCD

Calcul du volume d’un tétraèdre

Exercice 1 : Détermine le volume de ce tétraèdre ABCS

Exercice 2 : Détermine le volume de ce tétraèdre régulier ABCD

Annuler la réponse

Annuler la réponse