En galère sur un exercice traitant des variables aléatoires discrètes ? Pas de panique ! Grâce à cet article vous pourrez préparer sereinement vos interrogations orales et écrites !
Si vous souhaitez renforcer davantage vos compétences, nos profs de maths sont là pour vous aider à maîtriser les épreuves de probabilité en prépa. 📈
Exercice : Variables aléatoires discrètes
⏰ Durée : 30 min
💪 Difficulté : niveau 1/3
Soient1.
2. Justifier que
3.
Corrigé de l’exercice : Variables aléatoires discrètes
1.
2. Les variables aléatoires
On utilise la formule des probabilités totales avec le système complet d’événements
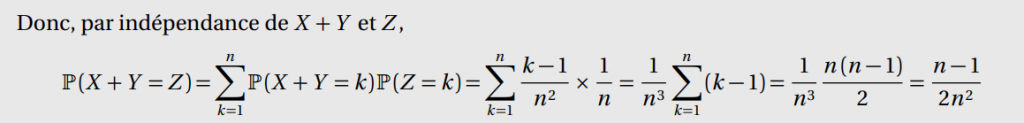
De plus, par le lemme des coalitions,

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720



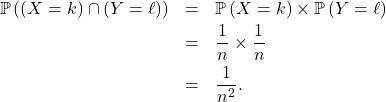
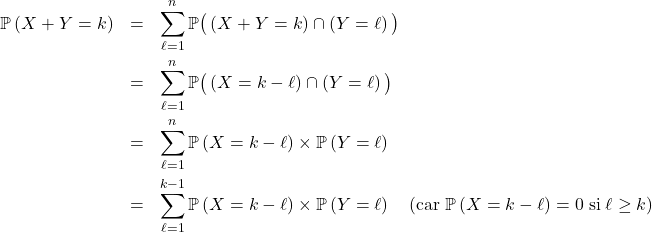
![Rendered by QuickLaTeX.com \[\mathbb{P} \left( X + Y = k \right) = \sum_{\ell=1}^{k - 1} \frac{1}{n} \times \frac1n = \frac{k - 1}{n^2}.\]](https://sherpas.com/content/ql-cache/quicklatex.com-ec4661cc5ac6176cad984914f741b6a1_l3.png)
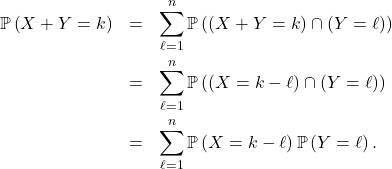
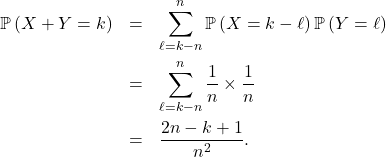
![Rendered by QuickLaTeX.com \[\mathbb{P} \left( X + Y = Z \right) = \sum_{k=1}^n \mathbb{P} \left( \left( X + Y = Z \right) \cap \left( Z = k \right) \right) = \sum_{k=1}^n \mathbb{P} \left( \left( X + Y = k \right) \cap \left( Z = k \right) \right).\]](https://sherpas.com/content/ql-cache/quicklatex.com-0bd1afd4dee32c43a4f02a195c8b2921_l3.png)










