Tout savoir sur le système linéaire

William Mievre - Mis à jour le 10/05/2022

Vous avez du mal avec la notion de système linéaire ? Pas d’inquiétude ! Grâce à ce cours dédié à la notion de système linéaire, familiarisez-vous davantage avec des méthodologies bien structurées qui vous permettront de décrocher de bonnes notes à vos prochaines interrogations orales et écrites !

Et si les inconnues et les rangs de matrices te semblent encore insurmontables, un prof particulier de maths peut transformer ce défi en une victoire mathématique. 🏆

Systèmes linéaires

Proposition

L’ensemble des solutions d’un système linéaire homogène à $n$

équations et $p$

inconnues est le noyau de la matrice des coefficients du système.

Démonstration

On considère le système linéaire homogène à $n$

équations et $p$

inconnues :

$(\mathcal{S})\, \left\lbrace \begin{array}{cccccccc} a_{1,1} x_1 &+& \dots &+& a_{1,p} x_p&=&0\phantom{.}\\ \vdots&&&&\vdots&&\vdots\\ a_{n,1} x_1 &+& \dots &+& a_{n,p} x_p&=&0.\\ \end{array}\right.$

On note $A=(a_{i,j})_{\substack{1\leq i\leq n\\ 1\leq j\leq p}}$

la matrice associée au système. Par définition, $(x_1,\dots,x_p)$

est solution de $(\mathcal{S})$

si, et seulement si, $A \begin{pmatrix} x_1\\\vdots\\x_p \end{pmatrix}=\begin{pmatrix} 0\\\vdots\\0 \end{pmatrix}$

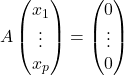. Autrement dit, l’ensemble des solutions de $(\mathcal{S})$

est $\mathrm{Ker}(A)$

Définition : Rang d’un système

Le rang d’un système linéaire homogène est le rang de la matrice de ses coefficients.

Proposition

La dimension de l’ensemble des solutions d’un système linéaire homogène à $n$

équations et $p$

inconnues de rang $r$

est égal à $p-r$

Démonstration

On note $A\in\mathcal{M}_{n,p}(\mathbb{K})$

la matrice des coefficients du systèmes. On sait que $\mathrm{dim}(\mathrm{Ker}(A))=p-\mathrm{rg}(A)$

.
Or, $\mathrm{Ker}(A)$

est l’ensemble des solutions du système.

Proposition

On considère un système linéaire dont l’écriture matricielle est $A\times X=B$

où $A\in\mathcal{M}_{n,p}(\)mathbb{K}$

, $X\in\mathcal{M}_{p,1}(\mathbb{K})$

et $B\in\mathcal{M}_{n,1}(\mathbb{K})$

.
Le système $A X=B$

est compatible si, et seulement si $B\in\mathrm{Im}(A)$

Démonstration

Conséquence immédiate de la définition de $\mathrm{Im}(A)$

Remarque : Structure affine de l’ensemble des solutions d’un système linéaire

Soit $A\times X=B$

un système compatible. On note $X_0$

une solution particulière du système.
Un vecteur $X$

est solution du système si, et seulement si, $AX=B$

.
Or, $AX_0=B$

. Donc, $X$

est solution du système si, et seulement si, $X-X_0\in\mathrm{Ker}(A)$

.
On en déduit que l’ensemble des solutions du système est le sous-espace affine de $\K^p$

dirigé par $\mathrm{Ker}(A)$

et passant pas $X_0$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720