Vous travaillez actuellement sur la notion de groupe symétrique ? À vous les bonnes notes ! Grâce à ce cours dédié à la notion de groupe symétrique, vous allez pouvoir bénéficier de méthodologies de pointe pour maîtriser cette notion sur le bout des doigts !
Et pour approfondir encore plus, déchiffre les mystères des permutations et des bijections avec l’aide d’un prof particulier d’algèbre en ligne ; ainsi, les bonnes notes ne seront plus qu’une formalité. 📝
Groupe symétrique
Définition : Groupe symétrique
SiOn vérifie facilement la proposition suivante
Proposition
Notation
Si
Attention !
Cette notation ressemble à une notation matricielle, mais il n’y a aucun lien entre les deux. Attention à ne pas les confondre !
Exemple
Soient
Proposition
SiDémonstration
On procède par récurrence surSupposons le résultat vrai pour tout couple d’ensembles
Soient
Pour tout
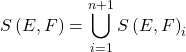 . Il s’ensuit que
. Il s’ensuit que

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720



![Rendered by QuickLaTeX.com \[\mathrm{card} \left( S \left( E, F \right) \right) = \sum_{i=1}^{n+1} \mathrm{card} \left( S \left( E , F \right)_i \right).\]](https://sherpas.com/content/ql-cache/quicklatex.com-7e20d36e4948299b8d66b1ba90668f2b_l3.png)
![Rendered by QuickLaTeX.com \[\mathrm{card} \left( S \left( E, F \right) \right) = \sum_{i=1}^{n+1} n! = \left( n + 1 \right) \times n! = \left( n + 1 \right)!.\]](https://sherpas.com/content/ql-cache/quicklatex.com-7b7ab6eae066dffbe3e96782d2aef0e1_l3.png)










