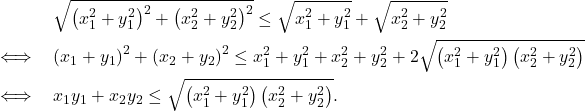Vous étudiez actuellement la topologie de R² ? Pas de panique ! Grâce à cette fiche de cours dédiée à la notion de topologie de R², vous pourrez maîtriser cette notion sur le bout des doigts !
Et si la topologie de R² vous semble toujours aussi abstraite que les dessins d’Escher, nos cours particuliers de maths peuvent éclairer votre compréhension et rendre cette abstraction en une réalité mathématique tangible. 🌀
Topologie de R²
Définition : Norme euclidienne sur R²
La norme euclidienne de
Proposition : Propriétés de la norme euclidienne
La norme euclidienne a les propriétés suivantes.Démonstration
Cette dernière inégalité est vraie : c’est l’inégalité de Cauchy-Schwarz dans
Définition : Boule ouverte
Soient
Définition : Ouvert de R²
Soit
Exemples
Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720