Qu'est-ce qu'un produit scalaire ?| Sherpas

Vous travaillez actuellement sur la notion de produit scalaire ? Grâce à ce cours dédié à la notion Qu’est-ce qu’un produit scalaire ?, maîtrisez tous les éléments liés à cette notion grâce à des méthodologies complètes !

Explorez plus en détail les subtilités et la beauté des produits scalaires avec nos cours de soutien en mathématiques, parfait pour exceller dans les espaces préhilbertiens et euclidiens. 💡

Produit scalaire

Définition : Produit scalaire

Soit $\varphi : E \times E \to \mathbb{R}$

une application. On dit que $\varphi$

est un produit scalaire sur $E$

si :

$\varphi$

est linéaire à gauche : pour tout $y \in E$

, $x \mapsto \varphi \left( x, y \right)$

est linéaire ;

$\varphi$

est linéaire à droite : pour tout $x \in E$

, $y \mapsto \varphi \left( x, y \right)$

est linéaire ;

$\varphi$

est symétrique : pour tout $\left( x, y \right) \in E^2$

, $\varphi \left( x, y \right) = \varphi \left( y , x \right)$

;

$\varphi$

est positive : pour tout $x \in E$

, $\varphi \left( x, x \right) \ge 0$

;

$\varphi$

est définie : pour tout $x \in E$

, $\varphi \left( x, x \right) = 0$

si, et seulement si, $x=0$

Remarque

Par linéarité à gauche et à droite, pour tout $x\in E$

, $\langle 0,x\rangle=0$

et $\langle x,0\rangle=0$

Si une application est symétrique, alors la linéarité à gauche et à droite sont équivalentes.

Exemples

Les exemples suivants sont fondamentaux et à connaître.

Le produit scalaire canonique sur $E = \mathbb{R}^n$

est défini par :

$\forall \left( x, y \right) \in \mathbb{R}^n \times \mathbb{R}^n, \quad \varphi \left( x , y \right) = \sum_{k=1}^n x_k y_k,~où~ x=(x_1,\dots,x_n)~et~y=(y_1,\dots,y_n).$

En notant $X$

(resp. $Y$

) la matrice de $x$

(resp. de $y$

) dans la base canonique de $\mathbb{R}^n$

, on a $\varphi(x,y)={}^t\!X Y$

Si $E = \mathcal C^0 \left( \left[ a , b \right] , \mathbb{R} \right)$

, l’application $\varphi$

définie par :

$\forall \left( f , g \right) \in \mathcal C^0 \left( \left[ a , b \right] , \mathbb{R} \right) \times \mathcal C^0 \left( \left[ a , b \right] , \mathbb{R} \right), \quad \varphi \left( f, g \right) = \int_a^b f \left( t \right) g \left( t \right) \mathrm{d}t$

est un produit scalaire sur $\mathcal C^0 \left( \left[ a , b \right] , \mathbb{R} \right)$

Si $E = \mathcal M_{n,p} \left( \mathbb{R} \right)$

, l’application $\varphi$

définie par

$\forall \left( A , B \right) \in \mathcal M_{n,p} \left( \mathbb{R} \right) \times \mathcal M_{n,p} \left( \mathbb{R} \right) , \quad \varphi \left( A , B \right) = \mathrm{tr} \left( {}^t\!A B \right)$

est un produit scalaire sur $\mathcal M_{n,p} \left( \mathbb{R} \right)$

.
En notant $A=(a_{i,j})_{\substack{1\leq i\leq n \\ 1\leq j \leq p}}$

et $B=(b_{i,j})_{\substack{1\leq i\leq n \\ 1\leq j \leq p}}$

, on a : $\displaystyle\varphi \left( A , B \right) = \sum_{i=1}^n\sum_{j=1}^pa_{i,j}b_{i,j}.$

Si $E = \mathbb{R}_n \left[ X \right]$

, l’application $\varphi$

définie par

$\forall \left( P , Q \right) \in \mathbb{R}_n \left[ X \right]\times \mathbb{R}_n \left[ X \right] , \quad \varphi \left( P , Q \right) = \sum_{k=0}^n P^{\left( k \right)} \left( 0 \right) Q^{\left( k \right)} \left( 0 \right)$

est un produit scalaire sur $\mathbb{R}_n \left[ X \right]$

Le produit scalaire de $x$

et de $y$

est rarement noté $\varphi(x,y)$

. On le note $\left\langle x , y \right\rangle$

, $\left( x , y \right)$

ou plus simplement $x\cdot y$

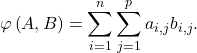
Remarque

Une récurrence immédiate montre que pour tous $\left( x_1, \dotsc, x_n \right) \in E^n$

et $\left( y_1, \dotsc, y_m \right) \in E^m$

, on a

$\left\langle \sum_{i=1}^n x_i , \sum_{j=1}^m y_j \right\rangle = \sum_{i=1}^n \sum_{j=1}^m \left\langle x_i , y_j \right\rangle.$

Conseils méthodologiques

Pour vérifier qu’une application $\varphi$

définie sur $E \times E$

est un produit scalaire sur $E$

, on vérifie les points de la définition.
Pour le caractère « définie », on utilisera fréquemment un argument du type : un polynôme est nul lorsqu’il a une infinité de racines ou une fonction continue positive sur un segment d’intégrale nulle est nulle, etc.

Définition : Espace préhilbertien réel

Soit $E$

un espace vectoriel sur $\mathbb{R}$

muni d’un produit scalaire. On dit que $E$

est un espace préhilbertien réel.
Si l’on suppose de plus que $E$

est de dimension finie, $E$

est alors un espace euclidien.

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720