Qu'est-ce que l'intégrale de Riemann ?

Qu’est-ce que l’intégrale de Riemann ?

William Mievre - Mis à jour le 08/06/2022

Sommaire

Intégrale d’une fonction en escalier

Vous travaillez actuellement sur l’intégrale de Riemann ? Grâce à ce cours dédié à la notion , l’intégrale de Riemann n’aura bientôt plus aucun secret pour vous ! Étudiez par exemple l’intégrale d’une fonction en escalier pour mieux comprendre ce chapitre et réussir vos interrogations à coup sûr !

Et si tu cherches à renforcer tes compétences, découvre nos cours de soutien en mathématiques et apprends à jongler avec les aires sous les courbes. 📐

Intégrale d’une fonction en escalier

Définition : Intégrale de Riemann d’une fonction en escalier

Soit $\varphi$

une fonction en escalier définie sur un intervalle $[a,b]$

et $(x_i)_{0\le i\le n}$

une subdivision adaptée à $\varphi$

telle que : $\forall i\in\ [[ 0,n-1]]$

, $\forall x\in]x_i,x_{i+1}[,\;\varphi(x)=\lambda_i$

.
On appelle intégrale de Riemann de la fonction en escalier $\varphi$

l’élément de $\mathbb{K}$

$\int_{[a,b]}\varphi =\sum_{i=0}^{n-1}\lambda_i(x_{i+1}-x_i).$

Remarques

La valeur de $\displaystyle \int_{[a,b]}\varphi$

ne dépend pas de la subdivision choisie.

Si $\varphi$

est à valeur réelle et $\varphi(x) \ge 0$

pour tout $x\in[a, b]$

alors $\lambda_i(x_{i+1}-x_i)$

est égal à l’aire du rectangle illustré sur la figure ci-contre.
Il vient naturellement que $\displaystyle\int_{[a,b]} \varphi$

représente l’aire de la portion du plan comprise entre la courbe et l’axe des abscisses si $\varphi$

est positive sur $[a,b]$

(l’opposé de l’aire si elle est négative). En effet, la formule revient à additionner l’aire des rectangles formés par la fonction en escalier.

Si $\varphi$

est une fonction constante égale à $M$

, alors : $\displaystyle\int_{[a,b]} \varphi=M(b-a)$

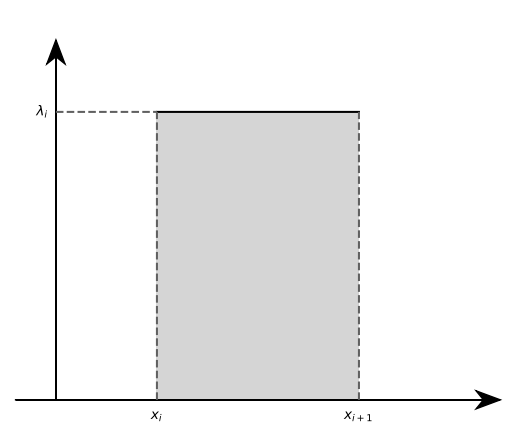
Forme canonique

Soient $f$

et $g$

deux fonctions en escaliers sur un intervalle $[a,b]$

. On remarque que $|f|$

est aussi une fonction en escaliers sur $[a , b ]$

Linéarité : Pour tout $(\lambda,\mu)\in\mathbb{K}^2$

, $\displaystyle \int_{[a,b]}(\lambda f+\mu g)=\displaystyle \lambda\int_{[a,b]}f+\mu\int_{[a,b]} g$

Inégalité triangulaire : $\displaystyle \left|\int_{[a,b]}f\right|\le \int_{[a,b]}\left|f\right|$

Relation de Chasles : Pour tout $c\in[a,b]$

, $\displaystyle \int_{[a,b]}f=\int_{[a,c]}f+\int_{[c,b]}f$

Croissance (on suppose ici que $\mathbb{K}=\mathbb{R}$

) : Si pour tout $x\in[a,b]$

, $f(x)\le g(x)$

alors : $\displaystyle \int_{[a,b]}f\le\int_{[a,b]}g$

Démonstration

Pas de difficulté dans cette preuve, la démonstration du premier point oblige de prendre une subdivision adaptée aux deux fonctions en escalier $f$

et $g$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720