Avez-vous des difficultés à calculer le rang d’une matrice ? Si c’est le cas, cet article est fait pour vous ! Nous allons vous guider à travers la méthode de calcul du rang d’une matrice, une compétence clé en algèbre.
👩🏫 En complément, approfondissez la théorie des matrices et leurs applications concrètes avec nos cours d’algèbre à domicile, spécialement conçus pour vous accompagner vers la réussite !
Méthode : Calculer le rang d’une matrice
Conseils méthodologiques
Pour déterminer le rang d’une matrice
En effet, à l’aide d’opérations élémentaires sur les lignes et colonnes, on peut passer de
Application de la méthode
Déterminons le rang de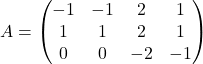 .
On a :
.
On a :
Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720



![Rendered by QuickLaTeX.com \[B=\begin{pmatrix} a_1 & * & \dots & \dots & \dots & \dots & * \\ 0 & a_2 & \ddots & & & & \vdots \\ \vdots & \ddots & \ddots & \ddots & & \vdots \\ \vdots & & \ddots & a_r & * & \dots & * \\ 0 & \dots & \dots & 0 & 0 & \dots & 0\\ \vdots & & & \vdots & \vdots & & \vdots\\ 0 & \dots & \dots & 0 & 0 & \dots & 0 \end{pmatrix}\]](https://adymrxvmro.cloudimg.io/v7/https://sherpas.com/content/ql-cache/quicklatex.com-6cd10dab033a5bd1e581733fa175f47c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{rcll} \mathrm{rg}\begin{pmatrix} \boxed{-1} & -1 & 2 & 1\\ 1 & 1 & 2 & 1\\ 0 & 0 & -2 & -1\end{pmatrix} & = & \mathrm{rg}\begin{pmatrix} \boxed{-1} & -1 & 2 & 1\\ 0 & 0 & 4 & 2\\ 0 & 0 & -2 & -1\end{pmatrix} & L_2\leftarrow L_2+L_1 \\ & = & \mathrm{rg}\begin{pmatrix} \boxed{-1} & 2 & -1 & 1\\ 0 & \boxed{4} & 0 & 2\\ 0 & -2 & 0 & -1\end{pmatrix} & C_2\leftrightarrow C_3 \\ & = & \mathrm{rg}\begin{pmatrix} \boxed{-1} & 2 & -1 & 1\\ 0 & \boxed{4} & 0 & 2\\ 0 & 0 & 0 & 0\end{pmatrix} & L_3\leftarrow L_3+\frac{1}{2}L_2 \\ & = & 2. \end{array}\]](https://adymrxvmro.cloudimg.io/v7/https://sherpas.com/content/ql-cache/quicklatex.com-78a39d78b9e4ae7592771547bcd996d9_l3.png)