Exercice corrigé matrice inverse

Sommaire

Exercices corrigés : Matrice inverse
Corrigés des exercices sur les matrices inverses

Pour être sûr d’avoir bien compris ce qu’est une matrice inverse, il est indispensable de s’entraîner en faisant des exercices. Ici, tu trouveras des exercices de différents niveaux ainsi que leur correction, de quoi devenir un vrai pro des mathématiques ! Deviens incollable sur la notion de matrice inverse !

Les exercices sur les matrices inverses te paraissent ardus ? Simplifie-les avec un cours particulier de maths en ligne sur-mesure. 🧮

Exercices d’application : Matrice inverse

Exercice 1 :

⏰ Durée : 10 min

💪 Difficulté : niveau 1/3

Montrer que les matrices suivantes sont inversibles et calculer leur inverse :

1. $A=\begin{pmatrix} 0 & -2 & 1\\ 1 & 0 & 1\\ 0 & -1 & 2\\ \end{pmatrix}$

2. $B=\begin{pmatrix} 1 & 2 & 1\\ 1 & 2 & -1\\ -2 & -2 & -1\\ \end{pmatrix}$

3. $C=\begin{pmatrix} 1 & \overline{\alpha} & \overline{\alpha}^2\\ {\alpha} & 1 & \overline{\alpha}\\ \alpha^2 & \alpha & 1\\ \end{pmatrix}$

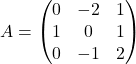
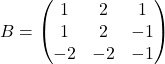
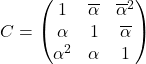
Exercice 2 :

⏰ Durée : 20 min

💪 Difficulté : niveau 3/3

Résoudre le système suivant en fonction de la valeur prise par le paramètre $\lambda \in \mathbb{R}$ .

$\left \{ \begin{array}{r c l} (-\frac{1}{2}-\lambda)x - \frac{1}{4}y + z & = & 0 \\ -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ 2x + 2y + (3-\lambda)z & = & 0 \end{array} \right$

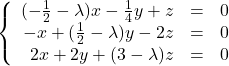
Corrigés des exercices d’application sur les matrices inverses

Exercice 1 :

On applique pour chaque matrice la méthode de Gauss-Jordan.

$1.\:A^{-1} = \frac{1}{3} \begin{pmatrix} 1 & 3 & -2 \\ -2 & 0 & 1 \\ -1 & 0 & 2 \end{pmatrix}$

$2.\:B^{-1} = \frac{1}{4} \begin{pmatrix} -4 & 0 & -4 \\ 3 & 1 & 2 \\ 2 & -2 & 0 \end{pmatrix}$

$3.$

La matrice C est inversible si et seulement si $|\alpha| \ne 1$

et $C^{-1} = \frac{1}{1-|\alpha|^2} \begin{pmatrix} 1 & -\bar{\alpha} & 0 \\ -\alpha & 1+|\alpha|^2 & -\bar{\alpha} \\ 0 & -\alpha & 1 \end{pmatrix}$

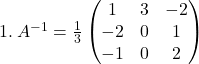
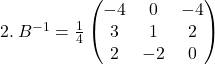
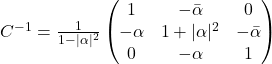
Exercice 2 :

Soit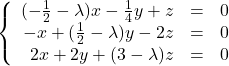 $\lambda \in \mathbb{R}$

:

$\left \{ \begin{array}{r c l} (-\frac{1}{2}-\lambda)x - \frac{1}{4}y + z & = & 0 \\ -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ 2x + 2y + (3-\lambda)z & = & 0 \end{array} \right$

$\Longleftrightarrow \left \{ \begin{array}{r c l} -x + (\frac{1}{2}-\lambda)y - 2z & = & 0\quad L_1 \leftrightarrow L_2 \\ (-\frac{1}{2}-\lambda)x - \frac{1}{4}y + z & = & 0\quad L_1 \leftrightarrow L_2 \\ 2x + 2y + (3-\lambda)z & = & 0 \end{array} \right$

$\Longleftrightarrow \left \{ \begin{array}{r c l} -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ (\lambda^2 -\frac{1}{2})y + (2+2\lambda)z & = & 0\quad L_2 \leftarrow L_2+(-\lambda-1/2)L_2 \\ (3-2\lambda)y - (\lambda+1)z & = & 0\quad L_3 \leftarrow L_3+2L_2 \end{array} \right$

$\Longleftrightarrow \left \{ \begin{array}{r c l} -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ (3-2\lambda)y - (\lambda+1)z & = & 0\quad L_3 \leftrightarrow L_2 \\ (\lambda^2-\frac{1}{2})y + (2+2\lambda)z & = & 0\quad L_3 \leftrightarrow L_2 \end{array} \right$

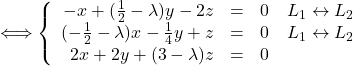
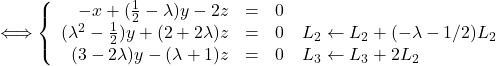
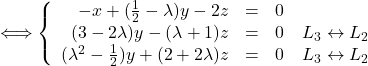
On va choisir $3-2\lambda$

comme pivot, cependant il est INTERDIT de choisir un pivot qui s’annule et $3-2\lambda = 0$

pour $\lambda = \frac{3}{2}$

. On va donc séparer deux cas :

On suppose que $\lambda = \frac{3}{2}$

. Alors :
$\left \{ \begin{array}{r c l} -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ (3-2\lambda)y - (\lambda+1)z & = & 0 \\ (\lambda^2-\frac{1}{2})y + (2+2\lambda)z & = & 0 \end{array} \right \Longleftrightarrow \left \{ \begin{array}{r c l} -x - y - 2z & = & 0 \\ \frac{5}{2}z & = & 0 \\ \frac{7}{4}y + 5z & = & 0 \end{array} \right$

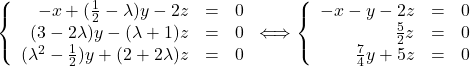
On en déduit que le système est de Cramer et que la seule solution est le triplet $(0,0,0)$

Supposons maintenant que $\lambda \in \mathbb{R}\backslash \{\frac{3}{2}\}$

, on choisit $3-2\lambda$

comme pivot :
$\left \{ \begin{array}{r c l} -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ (3-2\lambda)y - (\lambda+1)z & = & 0 \\ (\lambda^2-\frac{1}{2})y + (2+2\lambda)z & = & 0 \end{array} \right$

$\Longleftrightarrow \left \{ \begin{array}{r c l} -x + (\frac{1}{2}-\lambda)y - 2z & = & 0 \\ (\lambda^2-\frac{1}{2})y + (2+2\lambda)z & = & 0 \\ (\lambda^3-3\lambda^2+\frac{3}{2}\lambda+\frac{11}{2})z & = & 0\quad L_3 \leftarrow (3-2\lambda)L_3-(\lambda^2-1/2)L_2 \end{array} \right$

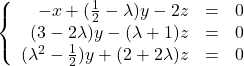
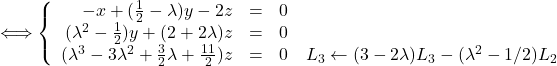
Le système est de Cramer si, et seulement si, ses pivots sont tous non nuls. On sait déjà que pour tout $\lambda \ne \frac{3}{2}$

les deux premiers pivots sont non nuls. On va résoudre :

$$\lambda^3-3\lambda^2+\frac{3}{2}\lambda+\frac{11}{2} = 0$.$

Pour cela factorisons le polynôme $P = X^3 - 3X^2 + \frac{3}{2}X + \frac{11}{2}$

.
$-1$

est une racine évidente. Donc il existe $a, b$

et $c$

trois réels tels que :

$$P = (X+1)(aX^2+bX+c).$

Ainsi :

$$P = aX^3 + (a+b)X^2 + (b+c)X + c$.$

Par identification des coefficients, on a : $a= 1, b= -4, c=\frac{11}{2}.$

Alors :

$$P = (X+1)(X^2-4X+\frac{11}{2}).$

Or le polynôme $X^2-4X+\frac{11}{2}$

n’admet aucune racine réelle (discriminant négatif). Donc l’équation $\lambda^3-3\lambda^2+\frac{3}{2}\lambda+\frac{11}{2} = 0$

n’admet que $-1$

comme solution réelle.
Pour tout $\lambda \in \mathbb{R}\backslash \{-1,\frac{3}{2}\}$

le système est de Cramer et admet une unique solution : $(0,0,0)$

.
Regardons ce qu’il se passe pour $\lambda=-1$

:

$\left \{ \begin{array}{r c l} -x + \frac{3}{2}y - 2z & = & 0 \\ \frac{1}{2}y & = & 0 \end{array} \right \Longleftrightarrow \left \{ \begin{array}{r c l} x & = & -2z \\ y & = & 0 \end{array} \right$

Dans ce cas il y a donc une infinité de solutions et l’ensemble solution sera :

$$\mathscr{S} = \{(-2z;0;z), z\in\mathbb{R}\}.$

Passe maître dans l’art de trouver la matrice inverse avec l’aide d’un soutien scolaire en maths assuré par l’un de nos professeurs particuliers. 🔍

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720