Vous étudiez actuellement la dérivée d’une fonction ? Grâce à ce cours de mathématiques dédié à la dérivée d’une fonction, vous allez pouvoir sereinement calculer les dérivées d’une fonction quelconque grâce à des méthodologies complètes !
Pour approfondir encore plus, maîtrise la dérivation et ses subtilités avec des cours de soutien en mathématiques et excelle dans le calcul des dérivées de fonction. 📚
Fonction dérivée
Définition : Dérivée d’une fonction
Soit
Exemples
Calculs de dérivées
Théorème
Soient
Démonstration
Soit
Remarque
Plus généralement, si
Corollaire
Soient
Remarque
Toute combinaison linéaire de fonctions dérivables surCorollaire
Une fonction polynomiale est dérivable surDémonstration
Pour toutThéorème
Soient
Démonstration
On sait que
Par composition des limites,
Donc, par opérations sur les limites,
Corollaire
Soient
Exemples
SoitCorollaire
SoientOn suppose que
Corollaire
SoitOn suppose que
Théorème
Soient
Corollaire
Soient
Exemples
Corollaire
Une fonction rationnelle sur tout intervalle où son dénominateur ne s’annule pas et sa dérivée est encore une fonction rationnelle.
Élève tes compétences en mathématiques à un niveau supérieur grâce à des cours de soutien en visio spécialisés sur la dérivée d’une fonction. 🚀

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720


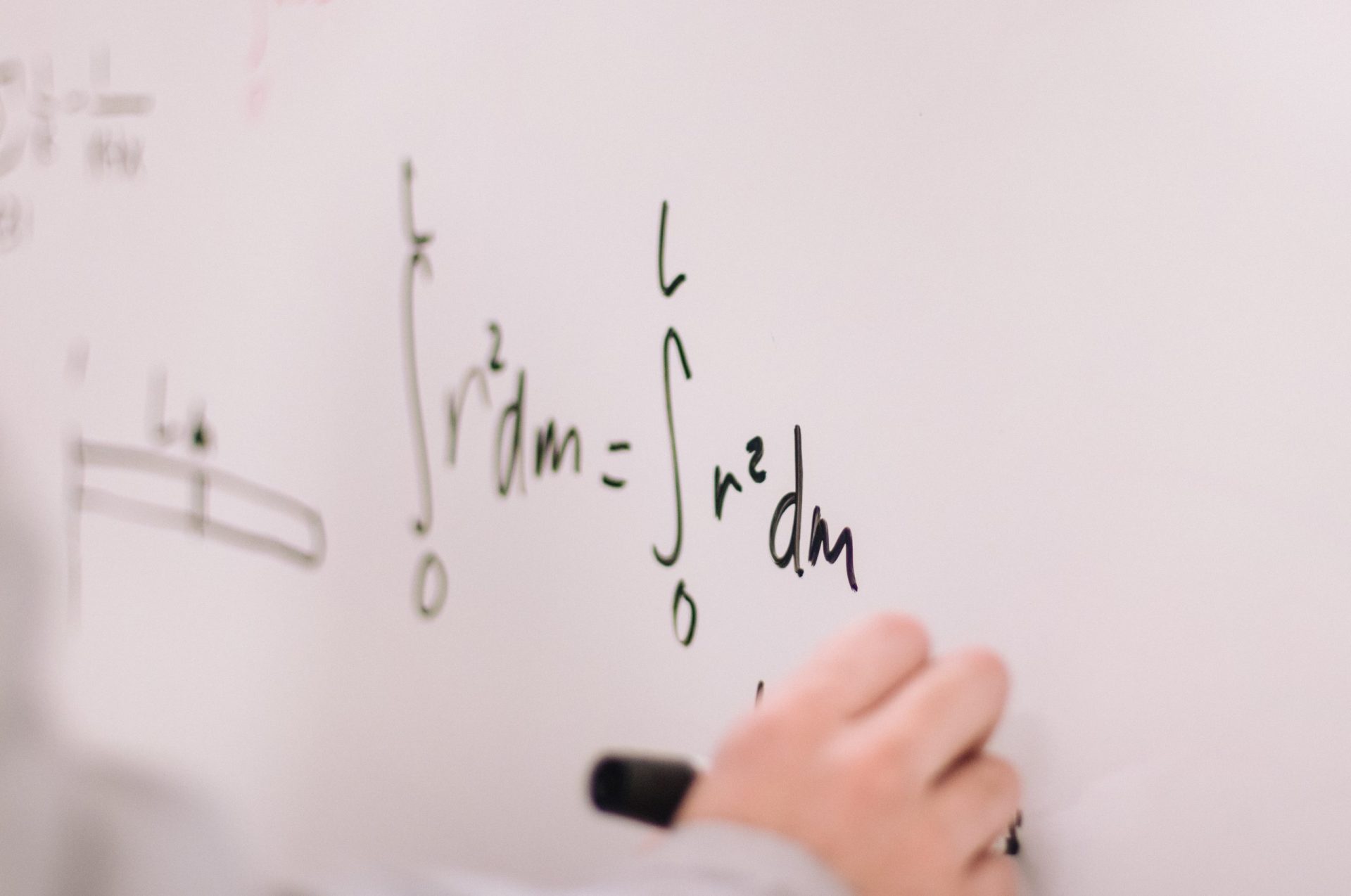
![Rendered by QuickLaTeX.com \[\left(\frac{f}{g}\right)'(a)=\frac{f'(a)g(a)-f(a)g'(a)}{\big(g(a)\big)^2}\]](https://sherpas.com/content/ql-cache/quicklatex.com-32d97843a1e7657fef8eb24614e0a9fe_l3.png)