Etude d'une fonction exponentielle

Vous souhaitez connaître les éléments essentiels relatifs à l‘étude d’une fonction exponentielle ? Sa dérivée, ses variations, ainsi que ses limites ? Grâce à ce cours de mathématiques dédié à l’étude d’une fonction exponentielle, répondez à toutes vos interrogations !

Et si jamais vous trouvez les variations de la fonction exponentielle ardues, sachez qu’elles peuvent être simplifiées avec l’aide d’un soutien scolaire en mathématiques personnalisé. 📈

La fonction exponentielle

La fonction $\ln$

est continue et strictement croissante sur $\mathbb{R}_+^*$

et $\ln(\mathbb{R}_+^*)=\mathbb{R}$

. D’après le théorème de la bijection, la fonction logarithme népérien réalise une bijection de $\mathbb{R}_+^*$

sur $\mathbb{R}$

. On appelle fonction exponentielle, notée $\exp$

, la bijection réciproque de la fonction logarithme népérien.

Proposition

La fonction $\exp$

est définie et de classe $\mathcal{C}^1$

sur $\R$

. Pour tout $x\in\R$

, on a :

$(\exp)'(x)=\exp(x).$

Démonstration

La fonction $\ln$

est dérivable sur $\mathbb{R}_+^*$

et sa dérivée ne s’annule pas sur $\mathbb{R}_+^*$

, donc sa fonction réciproque est dérivable sur $\mathbb{R}$

. Ainsi :

$\forall x\in\R, \;(\exp)'(x)=\dfrac{1}{(\ln)'(\exp(x))}=\dfrac{1}{1/\exp(x)}=\exp(x).$

La fonction $\exp$

est dérivable sur $\mathbb{R}$

, elle est donc continue sur $\mathbb{R}$

, ce qui justifie que $\exp$

est de classe $\mathcal{C}^1$

sur $\mathbb{R}$

Remarque

La définition même de la fonction exponentielle nous assure que : $\forall x\in\mathbb{R}$

, $\exp(x)>0$

Proposition

Pour tout $(x,y)\in\mathbb{R}^2$

, on a :

$\exp(x+y)=\exp(x)\times\exp(y)$

;

$\displaystyle\exp\left(-x\right)=\dfrac{1}{\exp(x)}$

;

Pour tout $x\in\R$

, $\exp(x)\ge 1+x$

;

$\forall n\in\Z$

, $\exp(x)^n=\exp(nx)$

;

$\displaystyle\exp\left(x-y\right)=\dfrac{\exp(x)}{\exp(y)}$

;

$\displaystyle\lim_{x\rightarrow -\infty}\exp(x)=0$

;

$\displaystyle\lim_{x\rightarrow +\infty}\exp(x)=+\infty$

Démonstration

Soient $(x,y)\in\mathbb{R}$

, on va montrer que : $\exp(x+y)=\exp(x)\times\exp(y)$

. On pose $a=\exp(x)$

et $b=\exp(y)$

de sorte que : $x=\ln(a)$

et $y=\ln(b)$

, ainsi :

$\exp(x+y)=\exp(\ln(a)+\ln(b))=\exp(\ln(ab))=ab=\exp(x)\exp(y).$

La relation $\displaystyle\exp\left(-x\right)=\dfrac{1}{\exp(x)}$

se déduit directement de la précédente. On montre la relation $\forall n\in\N$

, $\exp(x)^n=\exp(nx)$

par récurrence, on en déduit que cette relation est vraie pour $n\in\Z$

La relation $\displaystyle\exp\left(x-y\right)=\dfrac{\exp(x)}{\exp(y)}$

est une conséquence des deux premières relations.

On étudie les variations de la fonction $g:x\mapsto \exp(x)- (1+x)$

sur $\R$

Les limites se déduisent directement des limites de la fonction $\ln$

Notation

On note $\e=\exp(1)$

. En utilisant les propriétés de la fonction exponentielle, on peut montrer que pour tout $x\in\mathbb{R}$

: $\exp(x)=\e^x$

.
C’est cette notation qui sera privilégiée dans la suite.

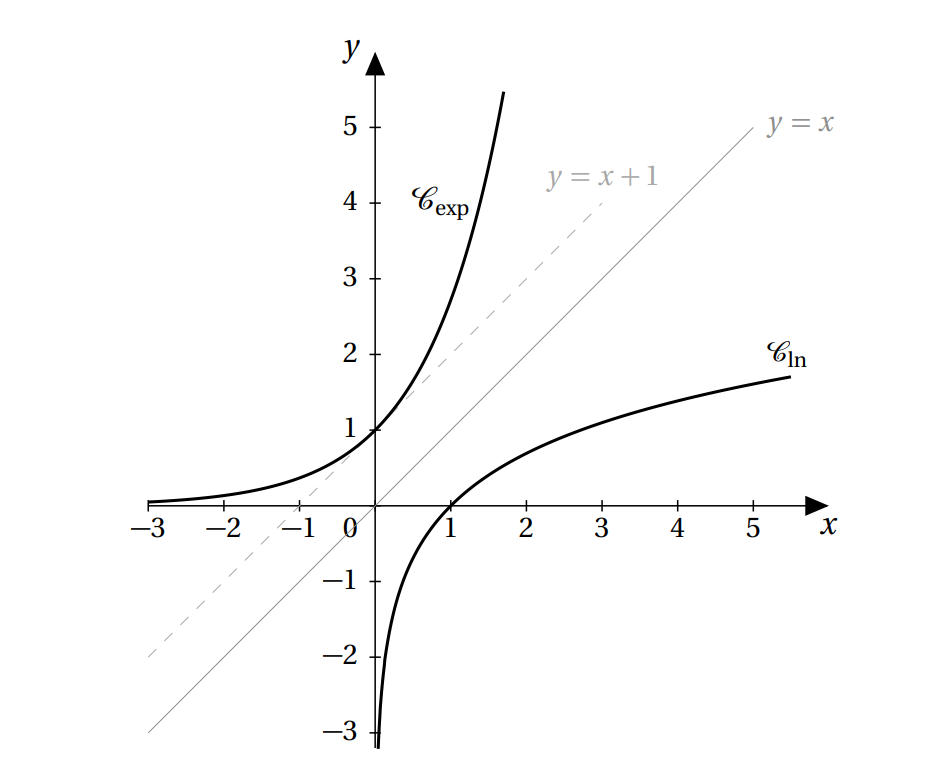
Voici la représentation graphique de la fonction exponentielle (c’est le symétrique de la courbe représentant la fonction ln par rapport à la droite d’équation y = x ) :

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720