Vous travaillez actuellement sur la convergence d’une suite ? Explorez cet article pour comprendre et maîtriser cette notion fondamentale en mathématiques, grâce à des méthodologies adaptées et des exercices corrigés.
Tu peines toujours à trouver la limite de tes suites ? 🎓 Perfectionne ta technique avec un cours particulier de maths, spécialement conçu pour les étudiants.
Exercice 1 : Convergence d’une suite
⏰ Durée : 20 min
💪 Difficulté : niveau 1/3
Étudier la convergence et calculer, si possible, la limite des suites suivantes :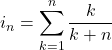 .
.
Corrigé de l’exercice 1 : Convergence d’une suite
1. On a
On factorise par le terme le plus grand :
Comme
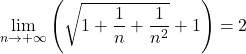 , on en déduit que
, on en déduit que
2. On a
La suite
3. On a
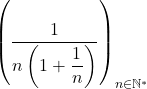 converge vers
converge vers 4. On a
On en déduit que la suite
5. On a :
la suite
Comme
6. On a :
7. On a :
8. On a
9. On commence par remarquer que si

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720



![Rendered by QuickLaTeX.com \[\forall n \in \mathbb{N}^*, \quad \dfrac{n + 1}{\sqrt{n^2 + n +1} + n} = \dfrac{n \left( 1 + \dfrac1n \right)}{n \left( \sqrt{1 + \dfrac1n + \dfrac{1}{n^2}} + 1 \right) } = \dfrac{1 + \dfrac1n}{\sqrt{1 + \dfrac1n + \dfrac{1}{n^2}} + 1}.\]](https://sherpas.com/content/ql-cache/quicklatex.com-b8917207613c263f43a717ff80a67dff_l3.png)
![Rendered by QuickLaTeX.com \[\forall n \in \mathbb{N}^*, \quad \dfrac{n \cos \left( n \right)}{n^2+1} = \cos \left( n \right) \times \dfrac{1}{n \left( 1 + \dfrac1n \right)}.\]](https://sherpas.com/content/ql-cache/quicklatex.com-7c8da6a94a68963faec5720eeb1ed655_l3.png)
![Rendered by QuickLaTeX.com \[\forall n \in \mathbb{N}^*, \quad n \tan \left( \dfrac1n \right) = \dfrac{\tan \left( \dfrac1n \right)}{\dfrac1n}.\]](https://sherpas.com/content/ql-cache/quicklatex.com-2f15ea50e77926edc4705a367e18a58d_l3.png)
![Rendered by QuickLaTeX.com \[\forall n \in \mathbb{N}^*, \quad i_n \ge \dfrac{1}{2n } \times \sum_{k=1}^n k = \dfrac{n+1}{4} \underset{n \to + \infty}{\longrightarrow} + \infty.\]](https://sherpas.com/content/ql-cache/quicklatex.com-82eed9f64832a4d3de0e19eb5f70db86_l3.png)










