Vous étudiez actuellement la convergence d’une série ? Grâce à ce cours dédié à la notion Comment montrer la convergence d’une série ?, grâce à une méthodologie bien rodée, réussi avec brio tes prochains exercices et contrôles sur cette notion !
Avant de plonger dans ton prochain contrôle, assure-toi aussi de maîtriser la convergence des séries avec l’aide d’un Sherpa expert en mathématiques par visio dédié à ton succès. 📘
Méthode 1 : Montrer la convergence d’une série et calculer sa somme
Montrons la convergence et calculons la somme de la série
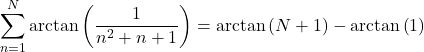 . Comme
. Comme 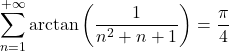 .
. 
Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720