Convergence des séries numériques exercice corrigé

Convergence des séries numériques : exercice corrigé

William Mievre - Mis à jour le 08/06/2022

Sommaire

Exercice 1 : Convergence séries numériques
Corrigé exercice 1 : Convergence séries numériques

En galère sur un exercice de convergence des séries numériques ? Obtiens des méthodologies complètes et adaptées grâce à cet article dédié à la notion.

Avant ta prochaine interro sur les séries, assure-toi d’être au top avec l’aide d’un prof particulier de maths en ligne qui saura te guider vers la réussite. 📚

Exercice 1 : Convergence des séries numériques

⏰ Durée : 20 min

💪 Difficulté : niveau 1/3

1. Montrer que la série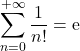 $\displaystyle{\sum_{n \ge 0} \frac{1}{n!}}$

converge. On admet que $\displaystyle{\sum_{n=0}^{+ \infty} \frac{1}{n!} = \mathrm{e}}$

.
2. Montrer que pour tout polynôme $P \in \mathbb{R} \left[ X \right]$

, la série $\displaystyle{\sum_{n \ge 0} \frac{P \left( n \right)}{n!}}$

converge. On note $S \left( P \right)$

sa somme.
3. Calculer $S \left( X + 1 \right)$

et $S \left( X^2 \right)$

Corrigé de l’exercice 1 : Convergence des séries numériques

1. Par croissances comparées, on a $\dfrac{1}{n!} \underset{n \to + \infty}{=} o \left( \dfrac{1}{n^2} \right)$

. Or, la s\’erie $\displaystyle{\sum_{n \ge 1} \frac{1}{n^2}}$

converge (série de Riemann), par négligeabilité, la série $\displaystyle{\sum_{n \ge 0} \dfrac{1}{n!}}$

converge.
2. Comme un polynôme est combinaison linéaire de monômes, il suffit de montrer que pour tout monôme $X^k$

, la série $\displaystyle{\sum_{n \ge 0} \frac{n^k}{n!}}$

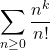converge. Or, $n^k \underset{n \to + \infty}{\sim} \dfrac{n!}{\left( n - k \right)!}$

, ainsi $\dfrac{n^k}{n!} \underset{n \to + \infty}{\sim} \dfrac{1}{\left( n - k \right)!}$

. Or, la série $\displaystyle{\sum_{n \ge k} \frac{1}{\left( n - k \right)!}}$

converge, par équivalence des séries à termes positifs, la série $\displaystyle{\sum_{n \ge 0} \dfrac{n^k}{n!}}$

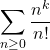converge.
3. Par relation de Chasles, on a :

$\begin{eqnarray*} \sum_{n=0}^{+ \infty} \dfrac{n+1}{n!} &=& \sum_{n=0}^{+ \infty} \frac{n}{n!} + \sum_{n=0}^{+ \infty} \frac{1}{n!} \\ &=& \sum_{n=1}^{+ \infty} \dfrac{1}{\left( n - 1 \right)!} + \sum_{n=0}^{+ \infty} \frac{1}{n!} \\ &=& \sum_{k=0}^{+ \infty} \frac{1}{k!}+ \sum_{n=0}^{+ \infty} \frac{1}{n!} \\ &=& 2 \mathrm{e}. \end{eqnarray*}$

On commence par remarquer que pour tout $n \in \mathbb{N}$

, $n^2 = n \left( n - 1 \right) + n$

. Ainsi :

$\begin{eqnarray*} \sum_{n=0}^{+ \infty} \dfrac{n^2}{n!} &=& \sum_{n=0}^{+ \infty} \frac{n\left( n - 1 \right)}{n!} + \sum_{n=0}^{+ \infty} \frac{n}{n!} \\ &=& \sum_{n=2}^{+ \infty} \dfrac{1}{\left( n - 2 \right)!} + \sum_{n=1}^{+ \infty} \frac{1}{\left(n - 1 \right)!} \\ &=& \sum_{k=0}^{+ \infty} \frac{1}{k!}+ \sum_{j=0}^{+ \infty} \frac{1}{j!} \\ &=& 2 \mathrm{e}. \end{eqnarray*}$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720