En galère sur le calcul du déterminant d’une matrice ? Pas de panique ! Notre cours spécifique te guidera à travers les étapes pour maîtriser cette technique complexe, te préparant ainsi pour réussir tes interrogations écrites et orales.
Et si tu souhaites peaufiner encore plus tes compétences, 🌟 deviens un as du calcul du déterminant et brille lors de tes prochaines évaluations avec l’aide de nos profs particuliers de maths expérimentés.
Calcul des déterminants
Opérations sur les déterminants
Proposition
SoitDémonstration : Déterminant d’une matrice
On note
Le déterminant est invariant par transposition. On a alors le résultat suivant.
Proposition
SoitPar récurrence, on montre alors le résultat suivant.
Corollaire
SoitDéfinition : Cofacteur
SoientLe cofacteur
Théorème
Soit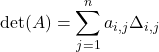 . On dit qu’on a développé le déterminant par rapport à la
. On dit qu’on a développé le déterminant par rapport à la Théorème
SoitSi
Autrement dit, le déterminant d’une matrice triangulaire est le produit de ses coefficients diagonaux.
Démonstration
On donne la démonstration dans le cas des matrices triangulaires supérieures.On raisonne par récurrence sur
Initialisation : immédiat.
Hérédité : soit
Soit
De plus, la matrice
Ce qui achève la récurrence. Si
Remarque

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720


![Rendered by QuickLaTeX.com \[\mathrm{det}(A)=a_{1,1}\times \begin{vmatrix} a_{2,2} & \cdots & a_{2,n+1}\\ \vdots & & \vdots\\ a_{n+1,2} & \cdots & a_{n+1,n+1} \end{vmatrix}_{(n)}.\]](https://sherpas.com/content/ql-cache/quicklatex.com-f6bd36e51c917edc9604ef6ad1bf69f4_l3.png)