Analyse asymptotique : exercice corrigé

Sommaire

Exercice : Analyse asymptotique
Corrigé de l’exercice

Besoin d’aide sur un exercice portant sur l’analyse asymptotique ? Pas de panique ! Grâce à ce cours dédié à la notion : analyse asymptotique : exercice corrigé, entraîne-toi avec des méthodologies bien rodées et réussis à coup sûr tes prochaines interrogations écrites et orales sur le sujet !

Optimise ton temps de révision grâce à un prof particulier de maths en ligne spécialisé en exercices d’analyse asymptotique. 🕒

Exercice : Analyse asymptotique

⏰ Durée : 15 min

💪 Difficulté : niveau 1/3

Déterminer un équivalent simple des suites définies par :

1. $u_n=\sqrt{n+1}-\sqrt{n-1}$

;

3. $u_n=a^n-b^n$

avec $(a,b)\in\big(\mathbb{R}_+^*\big)^2$

et $a\neq b$

2. $\displaystyle v_n=\frac{\left(e^{\frac{1}{n}}-1\right) \sin\left(\frac{1}{n^3}\right)}{\tan\left(\frac{1}{n}\right)\left(\sqrt[3]{1+\frac{1}{n}}-1\right)}$

;

Corrigé de l’exercice

1. En multipliant par la quantité conjuguée, on a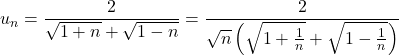 $\displaystyle u_n=\frac{2}{\sqrt{1+n}+\sqrt{1-n}}=\frac{2}{\sqrt{n}\left(\sqrt{1+\frac{1}{n}}+\sqrt{1-\frac{1}{n}}\right)}$

.
Or, par continuité de la fonction $\sqrt{\cdot}$

, on a $\displaystyle \sqrt{1+\frac{1}{n}}+\sqrt{1-\frac{1}{n}}\xrightarrow[n\to+\infty]{}2$

. Donc, $\displaystyle u_n\sim\frac{1}{\sqrt{n}}$

.
2. On a : $e^u-1\underset{u\to 0}{\sim}u$

, $\sin(u)\underset{u\to 0}{\sim}u$

, $\tan(u)\underset{u\to 0}{\sim}u$

et $\displaystyle\sqrt[3]{1+u}-1=(1+u)^{\frac{1}{3}}-1\underset{u\to 0}{\sim}\frac{u}{3}$

.
Or, $\displaystyle\frac{1}{n}\xrightarrow[n\to+\infty]{}0$

.
Donc, par substitution, $\displaystyle v_n \sim \frac{\frac{1}{n}\times \frac{1}{n^3} }{\frac{1}{n}\times \frac{1}{3n}}\sim \frac{3}{n^2}$

.
3. Il y a deux cas.
Cas 1 : $0<a<b$

. On a : $\displaystyle u_n=b^n\left(\left(\frac{a}{b}\right)^n-1\right)$

. Or, $\displaystyle \left|\frac{a}{b}\right|<1$

.
Donc, $\displaystyle \left(\frac{a}{b}\right)^n=o(1)$

.
Donc, $u_n=b^n(-1+o(1))$

, donc, $u_n\sim -b^n$

.
Cas 2 : $0<b<a$

. On a : $\displaystyle u_n=a^n\left(1-\left(\frac{b}{a}\right)^n\right)$

. Or, $\displaystyle \left|\frac{b}{a}\right|<1$

.
Donc, $\displaystyle \left(\frac{b}{a}\right)^n=o(1)$

.
Donc, $u_n=a^n(1+o(1))$

, donc, $u_n\sim a^n$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

Tu as aimé cet article ?

Sommaire

Exercice : Analyse asymptotique
Corrigé de l’exercice

Sur le même sujet

Comment exploser tes épreuves de maths en prépa HEC ? 💥

Calcul pourcentage : fiche de maths

Loi de Poisson : fiche de maths 🔢

Ton premier cours est offert ! 🎁

4 points de plus sur ta moyenne en prenant des cours particuliers avec l’un de nos Sherpas ! 👇

William Mievre

Co-fondateur des Sherpas

Passé par une Prépa HEC puis l'ESCP, j'ai donné des centaines d'heures de cours particuliers avant de créer Les Sherpas avec Étienne. Passionné d'éducation, je te partage désormais mes meilleurs conseils afin de t'aider à réussir et t'épanouir dans tes études. Cheers ✌️💖 !

Prépa Prépa scientifique

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉

Annuler la réponse

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉