Est-ce que tu sais ce qu’est un parallélogramme ? Cette forme géométrique incroyablement intéressante par toutes ses propriétés ! Dans cet article, on part à sa découverte pour comprendre comment il est utilisé dans la vie de tous les jours ! Alors, prêt à te plonger dans le monde captivant de cette forme géométrique 😁 ? C’est parti !
Qu’est-ce qu’un parallélogramme ? 🤔
Un parallélogramme, c’est un quadrilatère (un mot un peu compliqué pour désigner une figure à quatre côtés) avec des propriétés particulières !
Comment reconnaître un parallélogramme ?
Du coup, tu te demandes sûrement comment reconnaître un parallélogramme parmi tous les quadrilatères ? Eh bien, on recense 4 propriétés qu’il faut vérifier qu’on t’illustre avec un exemple 👇
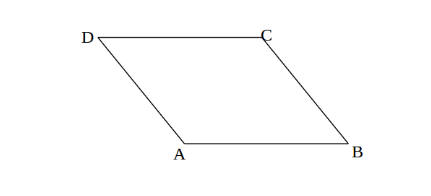
On a les points A, B, C et D qui forment un quadrilatère. On te dit que c’est un quadrilatère, mais tu veux vérifier s’il s’agit vraiment d’un parallélogramme en examinant ses propriétés !
1️⃣ Les côtés opposés sont parallèles.
Regarde les côtés AB et CD. Si ces côtés sont parallèles, cela signifie que les segments AD et BC devraient également être parallèles. Utilise ensuite un rapporteur pour mesurer les angles entre AD et BC et AB et CD. Si ces angles sont égaux, cela confirme que les côtés opposés sont parallèles !
🤓 Le savais-tu ?
Eh oui, si tu montres que les angles opposés d’un quadrilatère sont de mêmes mesures (comme ∠A = ∠C et ∠B = ∠D), cela indique que les côtés opposés sont en fait parallèles (comme AB || CD et BC || AD). C’est une règle géométrique essentielle !
2️⃣ Les côtés opposés ont la même longueur.
Mesure les longueurs des côtés opposés AB et CD, ainsi que AD et BC, à l’aide d’une règle. Si ces longueurs sont égales, alors cette propriété est vérifiée !
3️⃣ Les angles opposés sont égaux.
Mesure les angles entre les côtés AB et CD, et entre AD et BC, à l’aide d’un rapporteur. Si ces angles sont égaux, cela confirme la propriété !
4️⃣ Les diagonales se croisent en leur milieu.
Trace les diagonales AC et BD, puis utilise une règle pour mesurer la distance entre les points où elles se croisent. Si cette distance est égale à la moitié de la longueur de AC ou BD, alors cette propriété est vérifiée !
Il faut savoir que ces propriétés entraînent :
👉 Un centre de symétrie en tant que point d’intersection de ses diagonales
👉 Des angles consécutifs supplémentaires (leur somme est égale à 180°C) !
👀 Le savais-tu ?
Des angles consécutifs, parfois appelés angles adjacents, sont des angles qui partagent un côté commun et qui ont un sommet commun, mais qui ne se chevauchent pas !


Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Les différents types 🔷◼️
Tu te demandes certainement quels sont les différents types de parallélogrammes et ce qui les distingue. Eh bien, on t’explique tout en détail 👇.
Le rectangle ⬜
Imagine un rectangle comme une variante du parallélogramme où les angles sont tous droits, c’est-à-dire de 90 degrés ! Les côtés opposés sont aussi parallèles, et leurs longueurs sont égales. En gros, un rectangle a toutes les caractéristiques d’un parallélogramme, mais avec des angles bien droits !
Le carré ◼️
Maintenant, imagine un carré comme une version encore plus spéciale du rectangle. Tous les côtés du carré ont exactement la même longueur, et tous les angles sont droits, comme dans le rectangle. Donc, un carré est à la fois un rectangle et un parallélogramme !
Le losange 🔷
Voici le dernier membre de la famille des parallélogrammes : le losange. C’est un rectangle avec des côtés de même longueur, mais des angles qui ne sont pas forcément droits !
Peu importe le type, les propriétés de base restent les mêmes !
Calculer l’aire d’un parallélogramme 🧮
💡 Rappel : l’aire
L’aire est une mesure de la surface d’une forme géométrique. En gros, c’est la quantité d’espace occupée à l’intérieur de cette forme.
Par exemple, lorsque tu calcules l’aire d’une part de terrain, d’une salle, d’un rectangle, d’un cercle ou de tout autre objet en 2D, tu évalues la surface qu’il occupe. Elle est exprimée en unités carrées (m^2, l^2, cm^2…) !
Formule 🟰
Lorsqu’il s’agit de calculer l’aire d’un parallélogramme, c’est assez simple. Il suffit de multiplier la longueur de la base par la hauteur (la distance entre les bases parallèles).
La formule est donc 👇 :
Aire = base × hauteur.
Exemple 📖
On suppose que tu as le parallélogramme suivant ABCD
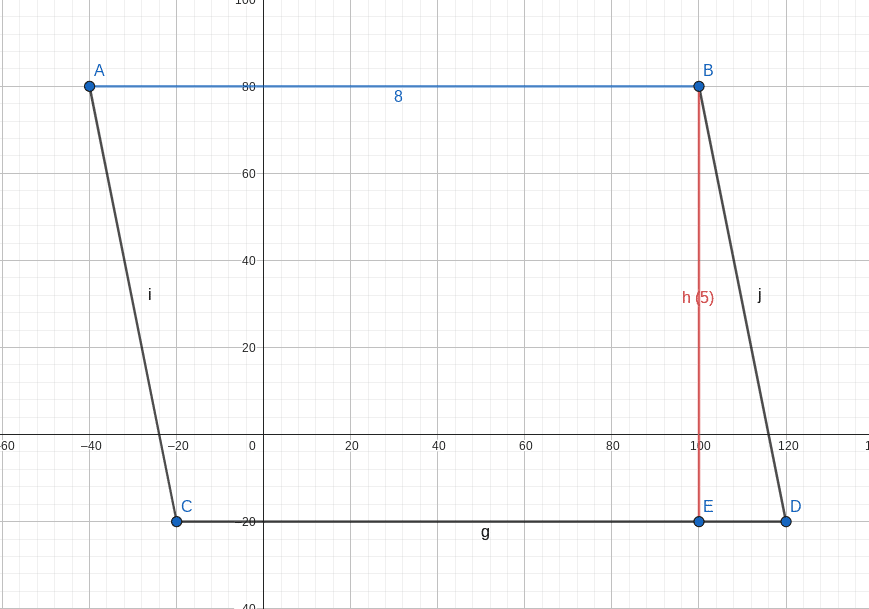
La base est le côté AB (ou CD) et la hauteur (H) est la distance entre les côtés AB et CD (ou AD et BC) !
AB = 8 unités
H = 5 unités.
Pour calculer l’aire, on utilise la formule suivante :
Aire = 8 unités × 5 unités = 40 unités carrées D
Donc, l’aire est de 40 unités carrées.


Ton premier cours particulier de maths est offert ! 🎁
Tous nos profs sont passés par les meilleures écoles de France !
Applications dans la vraie vie 😉
Les parallélogrammes ont de nombreuses applications pratiques dans la vie quotidienne et dans plein de domaines ! Voici quelques exemples 👇.
Architecture 🏠
Ils sont utilisés dans l’architecture et la construction pour créer des structures stables et esthétiques. Les portes et les fenêtres sont souvent encadrées dans des formes rectangulaires, et les poutres et les colonnes peuvent être conçues sous forme de parallélogrammes pour soutenir les charges !
Design et art 🎨
Les parallélogrammes, en particulier les rectangles et les carrés, sont utilisés dans le design d’intérieur et dans la création d’œuvres d’art pour obtenir des compositions équilibrées. Les tableaux, les cadres et les meubles rectangulaires sont des exemples courants !
Dans la nature 🌿
De nombreux cristaux et minéraux naturels ont des formes de parallélogrammes dans leur structure. Les cellules hexagonales des ruches d’abeilles en sont un exemple !

Ingénierie ⚙️
Les concepts de parallélogrammes sont utilisés en ingénierie pour résoudre des problèmes liés aux forces et aux déplacements. Par exemple, les mécanismes de levage et de pivotement peuvent être basés sur cette géométrie !
Exercice 🥊
Exercice 1 : Calcul d’aire
Tu as le parallélogramme ABCD suivant :
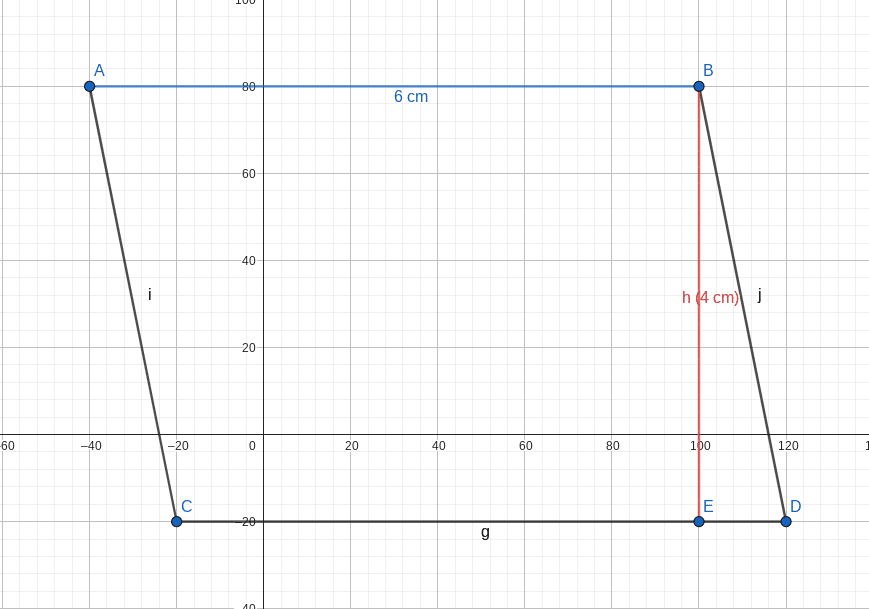
Les côtés AB et CD = 6 cm
H = 4 cm
Correction
L’aire se calcule en multipliant la longueur de la base (dans ce cas, AB ou CD) par la hauteur (H)
Aire = 6 cm × 4 cm = 24 cm²
Donc, l’aire est de 24 cm² !
Exercice 2 : Calcul d’aire
Tu as le parallélogramme EFGH suivant :
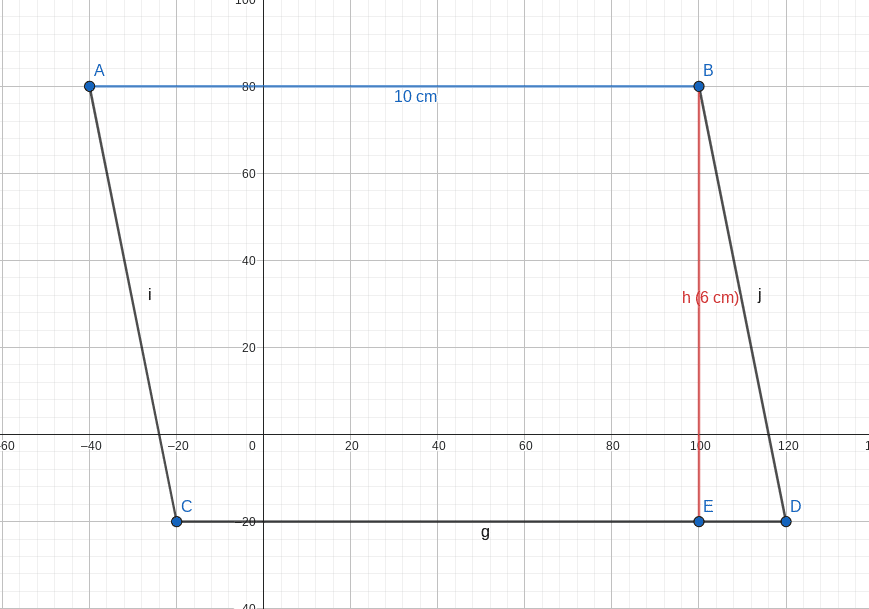
Les côtés EF et GH = 10 cm
H = 6 cm
Correction
L’aire se calcule en multipliant la longueur de la base (dans ce cas, EF ou GH) par la hauteur (H)
AAire = 10 cm × 6 cm Aire = 60 cm²
Donc, l’aire est de 60 cm².
Voilà, maintenant, tu sais tout le parallélogramme et leurs formules ! Retrouve nos autres fiches de cours de maths et n’hésite pas à contacter un prof particulier parmi nos Sherpas si tu as besoin d’aide ou que tu souhaites juste te perfectionner en maths !














