Lorsque tu entends les mots ‘racine carrée’, tu ne penses pas au super album de Stromae, mais plutôt au symbole mathématique. Ce qui est certain, c’est que les mathématiques te donnent davantage la migraine que les chansons du Belge ! 😰 Pour te changer la vie, on t’a concocté un cours sur les racines carrées. Grâce à ça, les théorèmes de Pythagore et de Thalès ne te poseront plus de problèmes ! 😆
Racine carrée, kezaco ?
Définition racine carrée
La racine carrée d’un chiffre correspond au résultat d’un nombre qui est multiplié par lui-même. En gros, la racine carrée, c’est le chiffre qui est à l’origine d’un carré. 😟
Voici un exemple pour que tu puisses mieux comprendre cette définition.
👉 Exemple : la racine carrée de 9, c’est 3 ! 3 x 3 = 9 ! Tu saisis ?
⚠️ Important
-
- Uniquement possible de calculer la racine carrée de nombres entiers positifs.
-
- Une racine carrée donne toujours un nombre positif. Il est impossible qu’une racine carrée donne un nombre négatif.
Aux origines de la racine carrée 🌍
La racine carrée est apparue pour la première fois au XXᵉ siècle avant Jésus-Christ. Oui, tu as bien compris, AVANT Jésus-Christ. Elle ne date pas d’hier ! 😱 Cependant, son symbole tel qu’on le connaît est apparu pour la première fois en 1525 grâce à Christoff Rudolff (un brillant mathématicien allemand du XVIᵉ siècle).
💡 On a choisi d’utiliser le terme de racine carrée car à l’origine, après avoir calculé l’aire d’un carré, on revenait en arrière (à la racine) pour trouver la longueur du côté.

À quoi sert la racine carrée ? 🤔
La racine carrée représente un chiffre mathématique. Par conséquent, elle est utilisée pour résoudre des équations du second degré ou faire des calculs. Ce n’est pas tout, elle est également présente et utile dans de nombreux théorèmes. En particulier ton préféré : le théorème de Pythagore. 😭
La racine carrée, une fonction 🚀
La racine carrée n’est pas uniquement utilisée dans les théorèmes de Thalès ou de Pythagore. Elle est aussi utilisée en tant que fonction. Ça ne te dit rien ? Bouge pas.
Définition de fonction racine carrée : la fonction racine carrée est la fonction “f” qui a tout nombre de son ensemble de définition associe la racine carrée de ce nombre.
Formule de la fonction racine carrée : f(x) = a√bx
👉 La courbe de la fonction racine carrée est croissante

Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Les racines carrées les plus courantes
Certaines racines carrées sont à connaître et à retenir pour éviter de les calculer à la machine en plein DST. Comme on pense à tout, les voici pour toi !👇
Le tableau des racines carrées parfaites ✨
| Racine carrée de | Formule | Résultat |
|---|---|---|
| Racine carrée de 0 | √0 | 0 |
| Racine carrée de 1 | √1 | 1 |
| Racine carrée de 4 | √4 | 2 |
| Racine carrée de 9 | √9 | 3 |
| Racine carrée de 16 | √16 | 4 |
| Racine carrée de 25 | √25 | 5 |
| Racine carrée de 36 | √36 | 6 |
| Racine carrée de 49 | √49 | 7 |
| Racine carrée de 64 | √64 | 8 |
| Racine carrée de 81 | √81 | 9 |
| Racine carrée de 100 | √100 | 10 |
| Racine carrée de 121 | √121 | 11 |
| Racine carrée de 144 | √144 | 12 |
| Racine carrée de 169 | √169 | 13 |
| Racine carrée de 400 | √400 | 20 |
Le tableau des racines carrées courantes
| Racine carrée de | Formule | Résultat |
|---|---|---|
| Racine carrée de 2 | √2 | 1,4 |
| Racine carrée de 3 | √3 | 1,7 |
| Racine carrée de 5 | √5 | 2,2 |
| Racine carrée de 10 | √10 | 3,1 |
| Racine carrée de 20 | √20 | 4,4 |
Les formules des racines carrées 🧐
Le tableau des formules des racines carrées
| √a² = a |
|---|
| √a x √b = √axb |
| √a / √b = √a/b |
| (√a)² = a |
Lors d’un calcul, tu peux être amené à utiliser ces formules. On te conseille donc de les apprendre par cœur. 💖
⚠️ Important
Lorsqu’une racine est associée à un carré, les deux s’annulent. Il ne reste plus que la valeur du chiffre ou du nombre.
👉 Exemple : (√9)² = 9
🖍️ Exercice
Dans cet exercice, tu devras utiliser les formules juste au-dessus pour réécrire les équations.
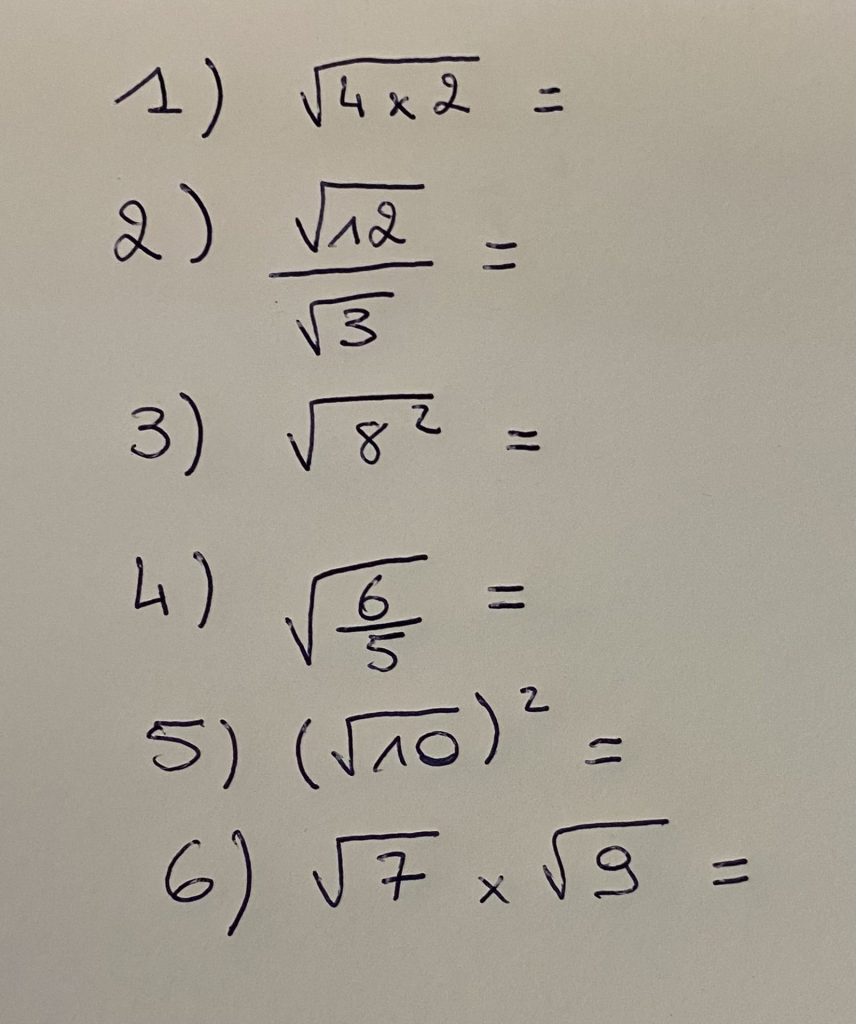
✅ Correction
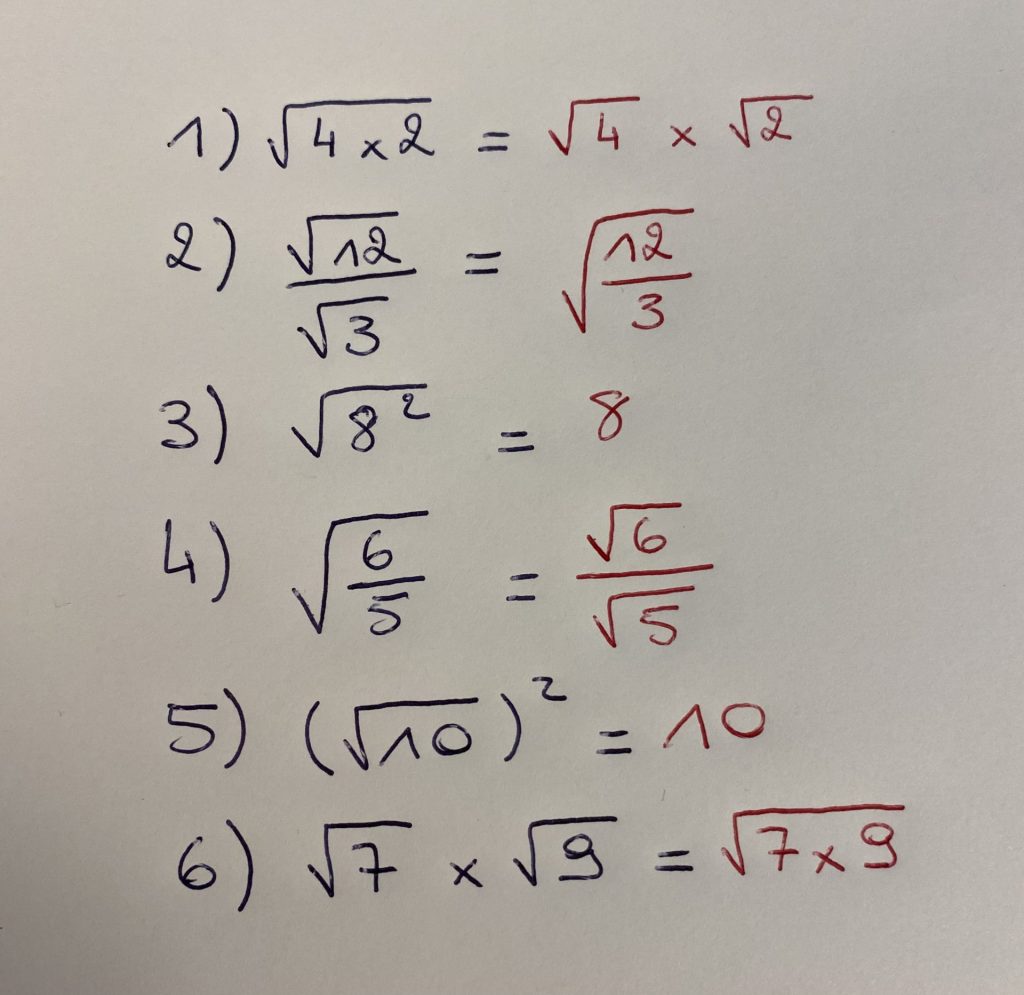
Ton premier cours particulier de maths est offert ! 🎁
Tous nos profs sont passés par les meilleures écoles de France !
Une méthode pour calculer la racine carrée sans calculatrice 🖐️
Il est clair que dans le siècle où les ordinateurs et les téléphones portables sont devenus rois, tu utilises la calculatrice pour faire tous tes calculs. Néanmoins, il vaut mieux être préparé à toutes les éventualités ! C’est pourquoi on a décidé de te présenter une technique qui te permettra de la calculer à la main. 🖐️ Oui, tu ne rêves pas. Allez, on te l’explique.
La méthode de l’encadrement successif :
Dans cet exemple, on souhaite trouver la racine carrée de 125 685.
1️⃣ 1ʳᵉ étape : Pour commencer, il va falloir trouver deux nombres qui, au carré, encadrent 125 685.
👉 Exemple :
- 300 au carré est égale à 90 000.
- 400 au carré est égale à 160 000.
- Donc : 90 000 < 125 685 < 160 000.
La racine carrée de 125 685 se situe forcément entre 300 et 400.
2️⃣ 2ᵉ étape : Maintenant que l’on sait dans quel intervalle se situe notre racine, il faut affiner le résultat. Pour ça, tu vas devoir réaliser deux soustractions.
La première sera entre le terme dont on cherche la racine carrée (ici 125 685) et le plus petit terme de l’encadrement (ici 90 000).
La seconde sera entre le plus grand terme de l’encadrement (ici 160 000) et le terme qu’on recherche (ici 125 685).
Ces deux calculs te permettent de voir où se situe ton nombre et donc de te rapprocher de sa racine carrée.
👉 Exemple :
- 125 685 – 90 000 = 35 685
- 160 000 – 125 685 = 34 315
Comme tu peux le constater, le résultat est presque le même dans les deux calculs. Cela signifie que la racine carrée de 125 685 se situe au milieu de l’intervalle 300-400.
3️⃣ 3ᵉ étape : Grâce aux calculs précédents, on sait que la racine carrée se situe au milieu de l’intervalle. Tu vas répéter le même procédé que lors de la première étape, en utilisant un encadrement plus précis.
👉 Exemple :
- 350 au carré est égale à 122 500.
- 360 au carré est égale à 129 600.
- 122 500 < 125 685 < 129 000.
4️⃣ 4ᵉ étape : Tu t’en doutes peut-être mais à partir de maintenant, tu vas devoir répéter le procédé jusqu’à trouver la valeur la plus proche ou exacte.
👉 Exemple :
- 354 au carré est égale à 125 316.
- 355 au carré est égale à 126 025
- 125 316 < 125 685 < 126 025.
On est tout proche du résultat !
Essayons de calculer le carré de 354,5.
- 354,5 au carré = 125 670.
Au vu de la proximité du résultat, on peut garder 354,5 comme racine carrée.
Le résultat exact était : 354,520.
💡 Verdict
Savoir calculer à la main sa racine carrée, c’est bien… Mais c’est quand même plus pratique et plus rapide à la calculatrice !
👉 Alors pense à ne pas l’oublier avant tes examens. Tu pourrais en avoir besoin. 😉
Ton premier cours particulier est offert ! 🎁
Nos profs sont passés par les meilleures écoles et universités.
Comment travailler les racines carrées ? 🤔
Maintenant que tu as mieux compris comment fonctionnait les racines carrées, il faut que tu t’entraînes. Parce que sinon, tu risques d’oublier tout ce que tu as retenu. Voici donc trois conseils qui te permettront d’ancrer la racine carrée au plus profond de ta mémoire.
👉 Faire une fiche de cours : cette petite astuce vieille comme le monde est pourtant toujours aussi efficace. Tu n’auras qu’à y renseigner toutes les formules des racines carrées qu’on t’a présentées, ainsi que les racines parfaites les plus importantes. 😁
👉 Faire des exercices : pour progresser, c’est ce qu’il y a de mieux ! Si Stephen Curry arrive à mettre autant de tirs à 3 points par match, c’est parce qu’il fait au moins 1000 shoots par jour. C’est ce que tu vas faire avec les racines carrées. Tu vas faire plein d’exercices pour les maîtriser (peut-être pas 1000 par jours hein 😉) ! Juste quelques-uns pendant plusieurs jours après avoir vu le cours.
👉 Faire appel à un Sherpa : si malgré les exercices, tu as encore un peu de mal avec les racines carrées, pas de panique. Il y a encore une solution pour toi : tu peux faire appel à l’un de nos super profs de mathématiques, un excellent complément à ton cours de maths ! L’un de nos professeurs saura répondre à ton problème et trouver la solution que tu espères tant ! 🤩
Ce petit guide sur les racines carrées est maintenant terminé. On espère que tu maîtriseras le sujet aussi bien que les chansons de l’album de Stromae. N’hésite pas à nous laisser un commentaire ! 😉