📒Les paraboles : cours et exos {Fiche de Maths}

Devinette ! Mon premier trace l’équation du second degré, mon deuxième peut sourire ou faire la grimace et mon tout est une courbe très connue en mathématiques. Eh oui, on veut évidemment parler de la parabole ! Apprends, révise et exercice-toi grâce à notre fiche de cours. Tu es prêt ? C’est parti ! 🚀

Une femme tient un tuyau en forme de parabole et dis que ce sont des maths.

Une parabole, c’est quoi ? 👀

Définition 📖

Une parabole est courbe qui représente une fonction polynôme du second degré.

Donc de la forme : $f(x)=ax^2+bx+c$ avec $a\neq0$

Représentation graphique de la parabole ✏️

Quand $a>0$ alors la parabole est tournée vers le haut.
Quand $a<0$ alors la parabole est tournée vers le bas.

Avec deux exemples, ça donne ça !

En abscisse on a les $x$ et en ordonnée les $y$ $(y=f(x))$ .

💡 Rappel

En abscisse on a les x et en ordonnée les y (y=f(x)).

La première coordonnée se lit sur l’axe des abscisses et la seconde se lit sur l’axe des ordonnées.

Coordonnée (x , y)
Coordonnée (abscisse , ordonnée)

Si tu confonds toujours les abscisses des ordonnées, voici un petit moyen mnémotechnique :

Moyen mnémotechnique pour les abscisses et les ordonnées.

Avec a>0

$f(x)=2x^2+x-2$

Et voici la parabole représentative de cette équation.

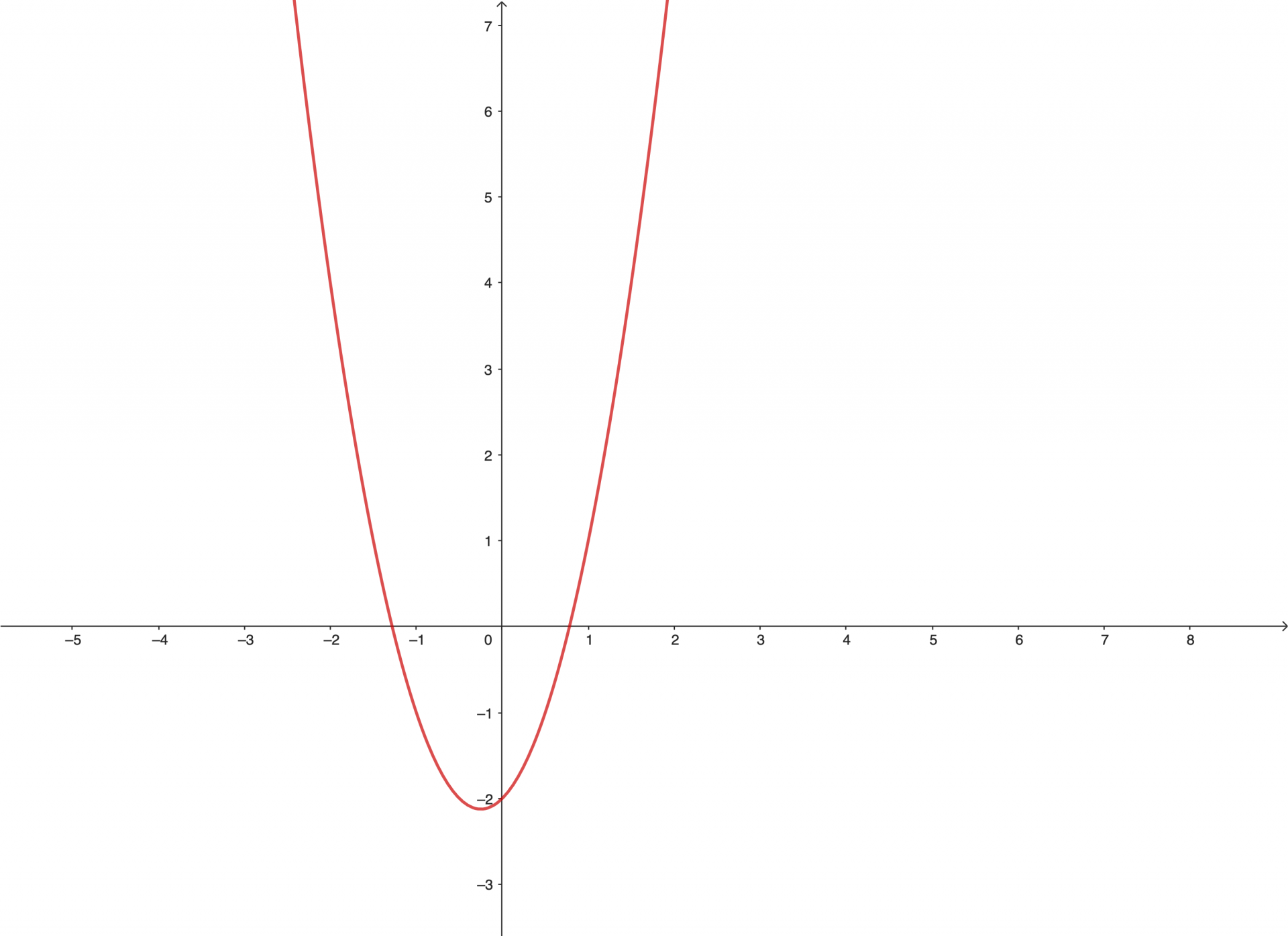
La parabole est convexe. Elle sourit 😊

Avec a<0

$f(x)=-3x^2+2x-1$

Et voici la parabole représentative de cette équation.

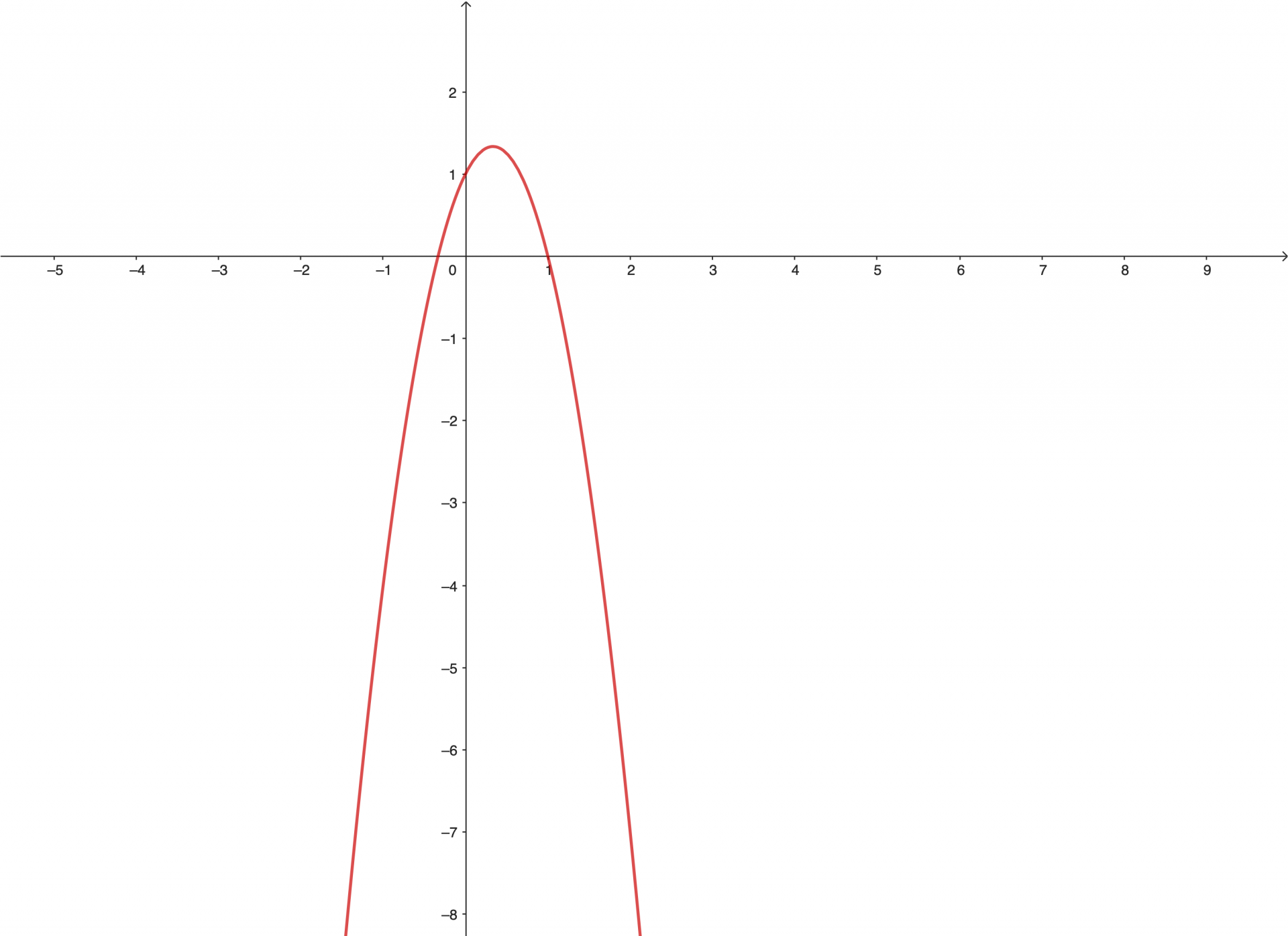
La parabole est concave. Elle fait la grimace ☹️

Tu galères en mathématiques ? Trouve ton prof particulier chez les Sherpas !

Thibault

ENS Paris Ulm

20€/h

Emilie

Sciences Po Lyon

19€/h

Clémence

HEC Paris

21€/h/h

Hugo

Insa Lyon

16€/h

Antoine

Sciences Po Paris

18€/h/h

Pierre

ESSEC

16€/h

Nicolas

CentraleSupélec

17€/h

Sophie

Sciences Po Bordeaux

12€/h

Ton premier cours particulier est offert ! 🎁

Nos profs sont passés par les meilleures écoles et universités.

J’EN PROFITE MAINTENANT !

Les notions à connaître 🧐

L’axe de symétrie

Dans une parabole, l’axe de symétrie est une droite imaginaire qui divise la parabole en deux parties symétriques.

Cette droite passe par le sommet de la parabole.

Mathématiquement, son équation est de la forme : $y=ax^2+bx+c$ s’écrit $x=\frac{-b}{2a}$

Le sommet

Le sommet de la parabole est le point le plus bas (dans le cas d’une parabole ouverte vers le haut) ou le point le plus haut (dans le cas d’une parabole ouverte vers le bas).

Si l’équation de la parabole est donnée sous la forme $y=ax^2+bx+c$ , les coordonnées du sommet peuvent être trouvées en utilisant les formules suivantes :
$(\frac{-b}{2a},\frac{4ac-b^2}{4a})$

Les différente formes d’une fonction du second degré 🤓

On peut écrire une équation du second degré de plusieurs formes.

Un homme dit que le diable a plusieurs formes. — *Toi avec les maths avant de connaître les Sherpas*

Forme développée

Écriture

$f(x)=ax^2+bx+c$

Sommet

$h=\frac{-b}{2a}$

$k=f(h)$

Zéros

Pour déterminer le(s) point(s) qui coupent l’axe des abscisses, il faut trouver le(s) racine(s) de l’équation.

En gros pour quel(s) $x$ , $y$ est égal à $0$ .

Une équation du second degré est une équation de la forme $ax^2+bx+c=0$ où $a$ , $b$ et $c$ sont des réels avec $a\neq0$

Une solution de cette équation s’appelle une racine du trinôme $ax^2+bx+c$
On appelle discriminant du trinôme $ax^2+bx+c$ , le nombre réel, noté $\Delta$
$\Delta=b^2-4ac$ .

Si $\Delta>0$ alors $ax^2+bx+c=0$ a deux solutions distinctes :
$x_1=\frac{-b-\surd{Delta}}{2a}$
$x_2=\frac{-b+\surd{Delta}}{2a}$

Si $\Delta=0$ alors $ax^2+bx+c=0$ a une unique solution :
$x_0=\frac{-b}{2a}$

Si $\Delta<0$ alors $ax^2+bx+c=0$ n’a pas de solution.

Forme factorisée

Écriture

$f(x)=a(x-x_1)(x-x_2)$

Sommet

$h=\dfrac{x_1+x_2}{2}$

$k=f(h)$

Zéros

$x_1$ et $x_2$

Effectivement si $x_1=x$ ou $x_2=x$ alors l’équation s’annule.

Forme canonique

Écriture

$f(x)=a(x-h)^2+k$

Sommet

$h$ et $k$

Zéros

$x=h\pm\sqrt[2]{\frac{-k}{a}}$

Clémence

HEC Paris

21€/h/h

Thibault

ENS Paris Ulm

20€/h

Sophie

Sciences Po Bordeaux

12€/h

Noémie

M2 en droit à Assas

19€/h

Fanny

Ponts ParisTech

19€/h

Simon

4e année de médecine

26€/h

Nicolas

CentraleSupélec

17€/h

Victor

ESCP

25€/h

Besoin d’un prof particulier ? ✨

Nos profs sont là pour t’aider à progresser !

JE PRENDS UN COURS GRATUIT !

Exercices ✍️

Si tu as bien compris le cours, tu devrais pouvoir résoudre ces exercices !

Une professeure fait un test de maths. — *À toi de jouer !*

Exercice 1

Représente graphiquement la fonction $f(x)=2x^2+2x+1$

Exercice 2

Détermine l’équation de cette parabole.

Corrigés 💯

Corrigé 1

$f(x)=2x^2+2x+1$

Détermine le sommet de la parabole à l’aide des coordonnées :

$(\dfrac{-b}{2a},\dfrac{4ac-b^2}{4a})$
$(\dfrac{-2}{2\times2},\dfrac{4\times2\times1-2^2}{4\times2})$

$(\dfrac{-2}{4},\dfrac{4}{8})$

$(\dfrac{-1}{2},\dfrac{1}{2})$

Choisis quelques valeurs de x et calcule les valeurs correspondantes de y en utilisant l’équation de la parabole pour placer ces points sur le graphique.

$f(-2)=2(-2)^2+2(-2)+1=8-4+1=5$
$f(-1)=2(-1)^2+2(-1)+1=2-2+1=1$
$f(0)=2(0)^2+2(0)+1=1$
$f(1)=2(1)^2+2(1)+1=5$

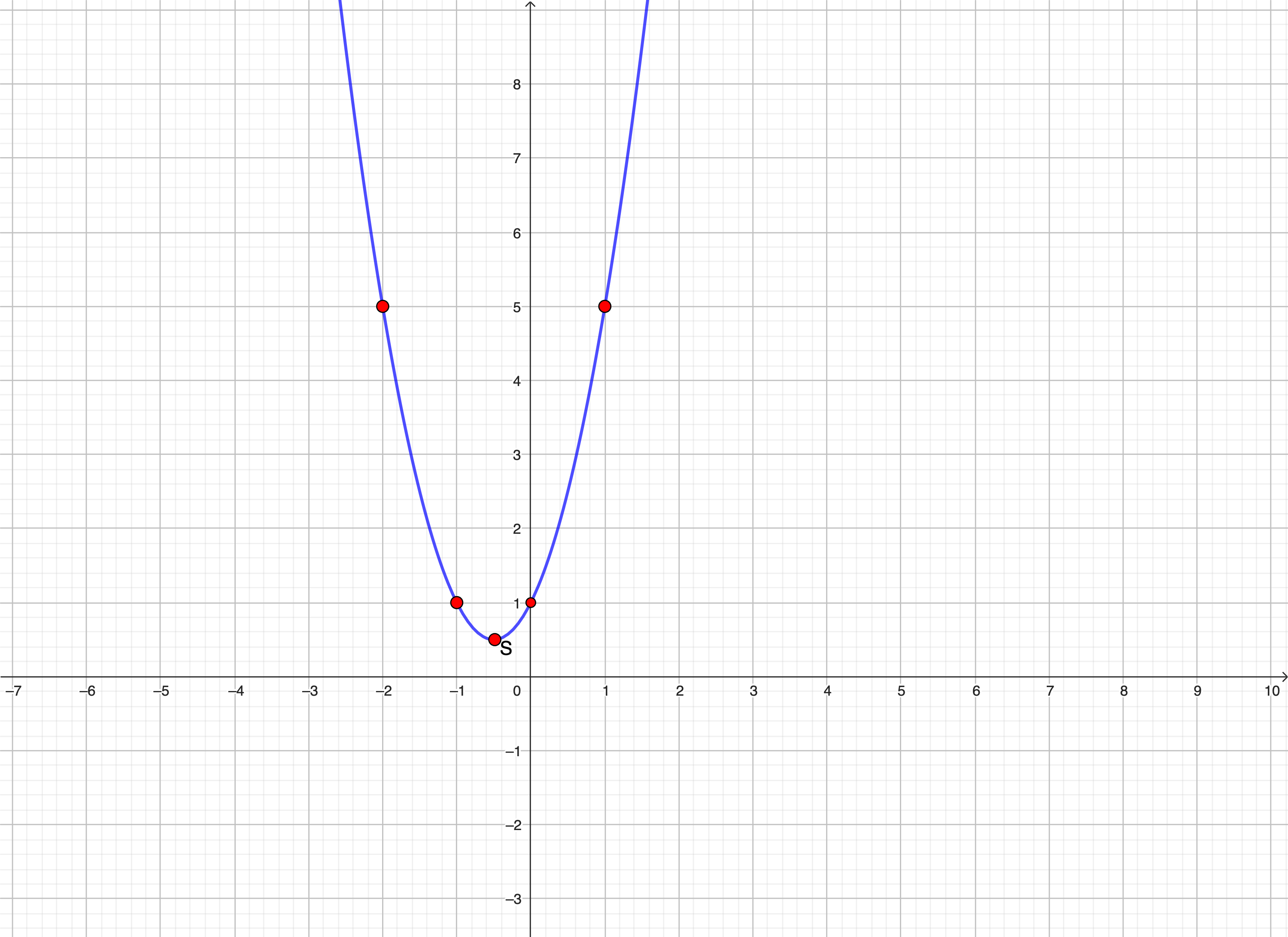
Si tu calcules le delta :

$\Delta=b^2-4ac$ .

$\Delta=2^2-4\times2\times1=4-8=-4<0$ .

Si $\Delta<0$ alors $ax^2+bx+c=0$ n’a pas de solution.

Donc la parabole ne coupe pas l’abscisse. Et c’est bien ce que nous avons représenté.

Corrigé 2

Pour cet exercice, on utilise la forme factorisée :

$f(x)=a(x-x_1)(x-x_2)$ où $x_1$ et $x_2$ sont les racines. La parabole coupe l’axe des abscisses en ces deux points.

$f(x)=a(x-x_1)(x-x_2)$
$f(x)=a(x-(-3)(x-1)$
$f(x)=a(x+3)(x-1)$

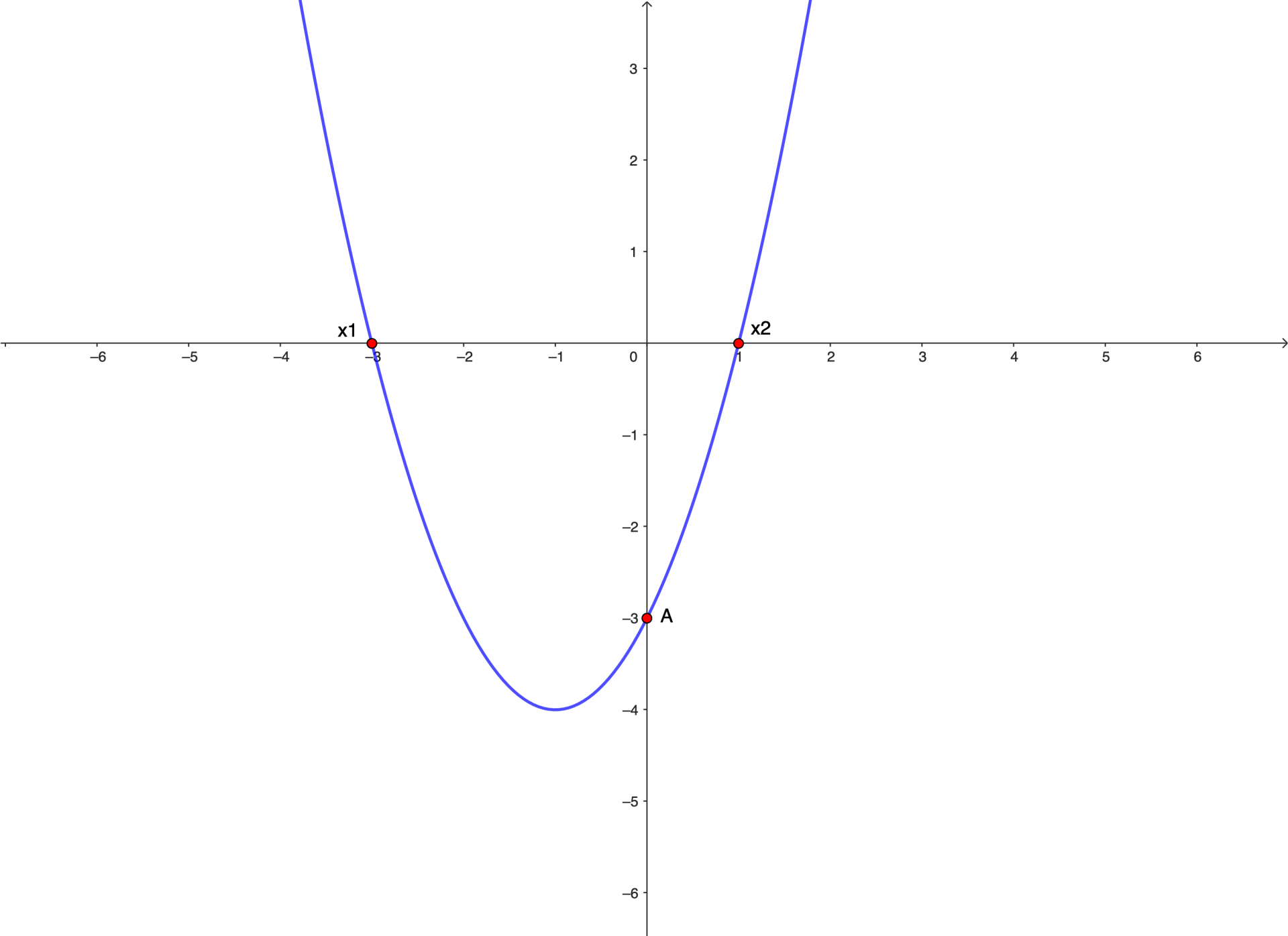
Pour trouver a, on utilise le point A de coordonnées (0;-3) qui appartient à la courbe et coupe l’axe des ordonnées en -3.

Quand $x=0$ alors $y=-3$

Et comme $f(x)=y$ alors $f(0)=-3$ .
On calcule $f(0)$

$f(0)=a(0+3)(0-1)$

$f(0)=a3\times-1=-3a$

Donc $-3a=-3$

$a=\dfrac{-3}{-3}=1$

On a donc : $f(x)=(x+3)(x-1)$

Pour retrouver la forme développée de l’équation, il suffit de la développer.

$f(x)=x^2-x+3x-3=x^2+2x-3$

Un homme dit que la mission est accomplie.

Voilà, notre fiche de cours sur la parabole est terminée ! On espère qu’elle t’aura aidé à mieux comprendre cette courbe. Si tu as des difficultés à comprendre et résoudre les exercices, n’hésite pas à prendre des cours de mathématiques avec un de nos Sherpas !

5/5 - (1 vote)

Paraboles : définition, calcul 🔢

Une parabole, c’est quoi ? 👀

Définition 📖

Représentation graphique de la parabole ✏️

Avec a>0

Avec a<0

Les notions à connaître 🧐

L’axe de symétrie

Le sommet

Les différente formes d’une fonction du second degré 🤓

Forme développée

Écriture

Sommet

Zéros

Forme factorisée

Écriture

Sommet

Zéros

Forme canonique

Écriture

Sommet

Zéros

Exercices ✍️

Exercice 1

Exercice 2

Corrigés 💯

Corrigé 1

Corrigé 2

Annuler la réponse

Annuler la réponse