Etude d'une fonction logarithme

Quels sont les points-clés de l’étude d’une fonction logarithme, les définitions et propriétés de base ? Ce cours de mathématiques va répondre à toutes ces questions et bien plus encore. Tu pourras également découvrir la dérivée de la fonction logarithme et savoir à quoi ressemblent ses variations, vers quelles limites elle tend. Continue de lire et bientôt les fonctions logarithme népérien n’auront plus aucun secret pour toi.

Définition de la fonction logarithme

On appelle fonction logarithme népérien, notée $\ln$

, l’unique fonction définie, continue et dérivable sur $\mathbb{R}_+^*$

s’annulant en $1$

, dont la dérivée est la fonction inverse.

On déduit de cette définition les propriétés suivantes :

Pour tout $(x,y)\in(\mathbb{R}_+^*)^2$

, on a :

$\ln(xy)=\ln(x)+\ln(y)$

;

$\displaystyle\ln\left(\dfrac{1}{x}\right)=-\ln(x)$

;

$\forall n\in\mathbb{Z}$

, $\ln\left(x^n\right)=n\ln(x)$

;

$\ln(x)\le x-1$

;

$\displaystyle\ln\left(\dfrac{x}{y}\right)=\ln(x)-\ln(y)$

;

$\displaystyle\lim_{x\rightarrow 0^+}\ln(x)=-\infty$

;

$\displaystyle\lim_{x\rightarrow +\infty}\ln(x)=+\infty$

Démonstration

On va montrer l’égalité $\ln(xy)=\ln(x)+\ln(y)$

. Soit $y\in\mathbb{R}_+^*$

, on considère la fonction $f:x\mapsto \ln(xy)-\ln(x)-\ln(y)$

. $f$

est dérivable sur $\mathbb{R}_+^*$

(comme composée de fonctions dérivables) et :

$\forall x\in\mathbb{R}_+^*,\;f'(x)=\dfrac{y}{xy}-\dfrac{1}{x}=0.$

La fonction $f$

est constante sur $\mathbb{R}_+^*$

, or $f(1)=0$

, d’où l’égalité recherchée.

On va montrer que pour tout $x\in\mathbb{R}_+^*$

, $\displaystyle\ln\left(\dfrac{1}{x}\right)=-\ln(x)$

. On remarque que pour tout $x\in\mathbb{R}_+^*$

: $x\times \dfrac{1}{x}=1$

, soit $\ln(x\times \dfrac{1}{x})=0$

. En utilisant le premier résultat : $\ln(x)+\ln(1/x)=0$

Pour montrer que : $\forall n\in\mathbb{N}$

, $\ln\left(x^n\right)=n\ln(x)$

, on procède par récurrence en utilisant le fait que : $\ln(x^2)=2\ln(x)$

. On généralise cette relation sur $\mathbb{Z}$

en utilisant la relation : $x^{-n}=\dfrac{1}{x^n}$

Pour montrer l’inégalité, on étudie les variations de la fonction $f:x\mapsto \ln(x)- (x-1)$

sur $\mathbb{R}_+^*$

Pour montrer l’égalité $\displaystyle\ln\left(\dfrac{x}{y}\right)=\ln(x)-\ln(y)$

, on utilise les relations précédentes.

Ces limites sont admises pour l’instant.

Tu galères en cours ? Essaie avec un professeur particulier de maths !

Représentation graphique de la fonction logarithme népérien

Définition
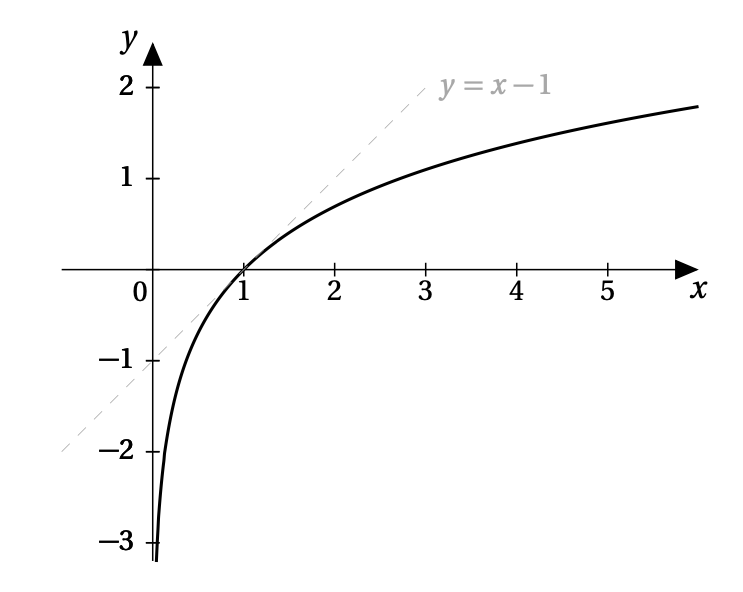
Soit $a>0$

, on définit le logarithme en base $a$

la fonction $\log_a:x\mapsto \dfrac{\ln(x)}{\ln(a)}$

Remarque : On note simplement le logarithme en base 10 : log. Cette fonction est notamment très utilisée en sciences de l’ingénieur ou en physique.

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

3.7/5 - (3 votes)

Étude d’une fonction logarithme

Définition de la fonction logarithme

Représentation graphique de la fonction logarithme népérien

Annuler la réponse

Annuler la réponse