Comment calculer la comatrice ?

William Mievre - Mis à jour le 29/05/2022

En galère sur un exercice de calcul de la comatrice ? Rassure-toi, grâce à ce cours entièrement dédié à la notion Comment calculer la comatrice ?, cette notion n’aura bientôt plus aucun secret pour toi ! Le 20/20 est assuré sur ta prochaine interrogation ! Et pour propulser tes compétences en algèbre à un niveau supérieur, apprends à maîtriser la comatrice avec des cours en ligne de mathématiques interactifs.

Comatrice

Définition : Comatrice

Soit $A\in\mathcal{M}_n(\mathbb{K})$

. La matrice $\big(\Delta_{i,j}\big)_{1\leq i,j\leq n}$

des cofacteurs de $A$

est appelée comatrice de $A$

et est notée $\mathrm{Com}(A)$

Proposition

Soit $A\in\mathcal{M}_n(\mathbb{K})$

.
On a ${}^t\mathrm{Com}(A)\times A=A\times{}^t\mathrm{Com}(A)=\mathrm{det}(A).I_n$

Démonstration

On note $A=(a_{i,j})_{1\leq i,j\leq n}$

. Soit $(i,j)\in [[1,n]]^2$

.
Le coefficient en position ligne $i$

colonne $j$

de ${}^t \mathrm{Com}(A)\times A$

est $\displaystyle\sum\limits_{k=1}^n \Delta_{k,i}a_{k,j}=\displaystyle\sum\limits_{k=1}^na_{k,j} \Delta_{k,i}.$

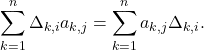
On note $B_{i,j}$

la matrice obtenue en remplaçant la $i$

-ème colonne de $A$

par la $j$

-ème.
Par développement par rapport à la $i$

-ème colonne, on a $\mathrm{det}(B_{i,j})=\displaystyle\sum\limits_{k=1}^na_{k,j}\Delta_{k,i}$

.
Si $i\neq j$

, alors les colonnes $i$

et $j$

de $B_{i,j}$

sont égales, donc, $\mathrm{det}(B_{i,j})=0$

. Si $i=j$

, alors $B_{i,j}=A$

, donc $\mathrm{det}(B_{i,j})=\mathrm{det}(A)$

.
Ainsi,

$\sum\limits_{k=1}^n \Delta_{k,i}a_{k,j} = \left\lbrace\begin{array}{cl} \mathrm{det}(A) & \text{si $i=j$}\\ 0 & \text{si $i\neq j$}. \end{array}\right.$

Donc, ${}^t\mathrm{Com}(A)\times A=\mathrm{det}(A).I_n$

. L’égalité $A\times {}^t\!\mathrm{Com}(A)=\mathrm{det}(A).I_n$

se montre de la même manière.

On a alors immédiatement le résultat suivant.

Corollaire

Soit $A\in\mathrm{GL}_n(\mathbb{K})$

. On a :

$A^{-1} = \frac{1}{\mathrm{det}(A)}.{}^t\mathrm{Com}(A).$

Cet article est extrait de l’ouvrage Maths MPSI-MP2I. Tout-en-un : cours, méthodes, entraînement et corrigés (éditions Vuibert, juin 2021) écrit par E. Thomas, S. Bellec, G. Boutard. ISBN n°9782311408720

1.5/5 - (2 votes)

Sommaire

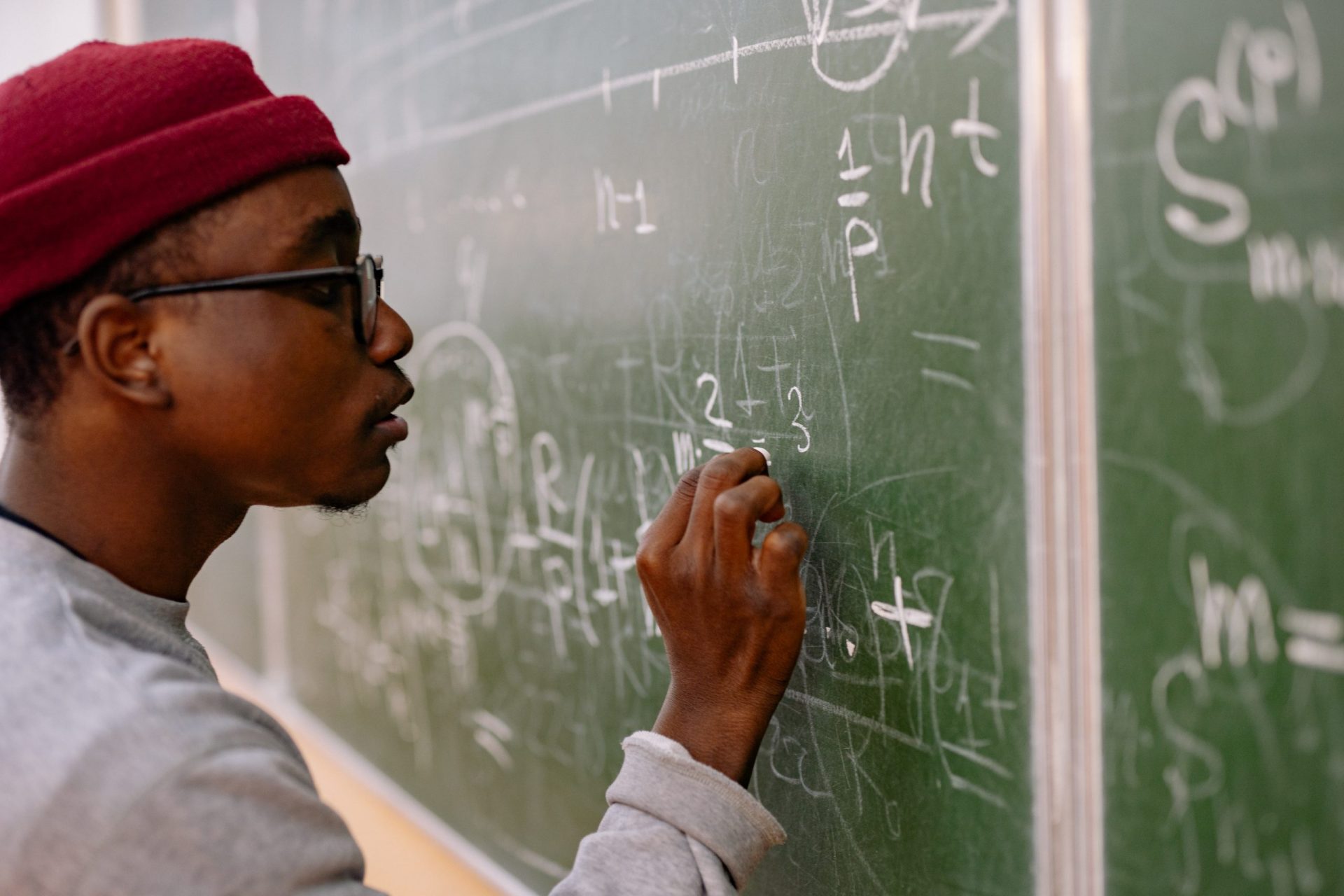
Comatrice

Sur le même sujet

Théorème de Thalès : quésaco ? 😲

Comment exploser tes épreuves de maths en prépa HEC ? 💥

Calcul pourcentage : fiche de maths

Ton premier cours est offert ! 🎁

+4,36 points sur la moyenne pour les élèves prenant des cours réguliers chez Les Sherpas ! 👇

William Mievre

Co-fondateur des Sherpas

Passé par une Prépa HEC puis l'ESCP, j'ai donné des centaines d'heures de cours particuliers avant de créer Les Sherpas avec Étienne. Passionné d'éducation, je te partage désormais mes meilleurs conseils afin de t'aider à réussir et t'épanouir dans tes études. Cheers ✌️💖 !

Prépa Prépa scientifique

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉

Annuler la réponse

Laisse-nous un commentaire !

Des questions ? Des bons plans à partager ? Nous validons ton commentaire et te répondons en quelques heures ! 🎉