Tu es passionné de jeux ou un vrai stratège en général ? Ne bouge pas ! On t’explique aujourd’hui ce qu’est la théorie des jeux. Des mathématiques à l’économie en passant par la psychologie, c’est un domaine passionnant qui te permet de prendre des décisions et de prévoir celles des autres. Dans cette fiche de cours, on t’explique les bases de cette discipline !
La théorie des jeux, c’est quoi ? 👀
Histoire 📚
Tout commence dans les années 20. Émile Borel, un mathématicien français, publie La théorie du jeu et les équations intégrales à noyau symétrique en 1928. Dans son livre, il introduit les jeux de stratégie et les équilibres. Émile Borel jette ainsi les bases de la théorie des jeux.
Mais ce n’est qu’en 1944 que la théorie des jeux a été popularisée par la publication de Theory of Games and Economic Behavior par John von Neumann, un mathématicien et physicien hongrois, et Oskar Morgenstern, un économiste autrichien. La théorie des jeux devient un domaine distinct de recherche !
Définition 📖
La théorie des jeux est un domaine des mathématiques et de l’économie qui étudie les comportements stratégiques et les interactions entre les individus quand ils doivent prendre une décision. On appelle les individus en question des “joueurs”. L’idée est d’analyser pour mieux comprendre les choix rationnels et prédire les résultats possibles.
↪️ Exemple
Tu joues au morpion avec ton ami John. Chacun doit choisir une action en fonction de l’autre. Vous devez tous les deux prendre des décisions en anticipant les actions de l’autre. Tu prédis les coups de ton adversaire et tu t’adaptes, et, s’il est aussi compétiteur que toi, John fait de même !
Eh bien, la théorie des jeux permet de comprendre comment toi et John pensez et comment vous prenez vos décisions lors du jeu.
Notions en théorie des jeux 📜
Pour qu’un jeu fonctionne en théorie des jeux, il faut respecter quelques critères. Eh oui, sinon c’est trop facile.
📌 Les jeux ont des règles : les interactions stratégiques sont modélisées à l’aide de jeux abstraits qui donnent les règles et les actions possibles des joueurs.
📌 Les joueurs sont rationnels : les joueurs cherchent à maximiser leur gains.
📌 Les choix sont stratégiques : les joueurs choisissent la stratégie la plus avantageuse pour eux.
📌 Les joueurs interagissent : les choix de chaque joueur influencent les résultats des autres joueurs.
Ton premier cours particulier est offert ! 🎁
Nos profs sont passés par les meilleures écoles et universités.
L’équilibre de Nash : concept clé en théorie des jeux
L’équilibre de Nash est une situation où aucun joueur n’a intérêt à changer de stratégie étant donné les choix des autres joueurs. C’est un état de stabilité ! En fait, chaque joueur prédit correctement la stratégie de l’autre et maximise son gain en fonction.
L’équilibre de Nash a été théorisé par le mathématicien et économiste John Nash.
💡 Le savais-tu ?
John Nash a reçu le prix Nobel d’économie en 1994 pour ses travaux sur la théorie des jeux.
Dans le film Un homme d’exception, l’équilibre de Nash est expliqué dans un bar dans une situation de drague. On t’explique !
Alors que John Nash se trouve dans un bar avec des amis, 4 femmes entrent. Les hommes sont tous attirés par une seule femme, la blonde.
Pour lancer le sujet, l’un des hommes cite Adam Smith : “Dans le cadre de la compétition, les ambitions individuelles servent la communauté.” En gros, chacun pour soi !
Mais John Nash n’est pas d’accord avec Adam Smith.
👉 S’ils attaquent tous la blonde ils se font tous rejeter. Ils vont se rabattre sur ses copines qui vont les rejeter aussi, car personne n’aime être un deuxième choix.
👉 Si personne n’attaque la blonde, ils ne se gênent pas les uns les autres et ne vexent pas les autres filles. Ils ont intérêt à choisir chacun une fille.
➡️ C’est le seul moyen de gagner et de ne pas finir la soirée seul !
En gros pour arriver à un résultat optimal, le groupe doit s’occuper d’eux individuellement mais du groupe aussi.
À lire aussi
🎞️ Découvre notre sélection des 7 films qui vont te faire aimer les maths !
Exemples en théorie des jeux
Jeu à somme nulle ⚽
En théorie des jeux, un jeu à somme nulle est un jeu dans lequel le gain d’un joueur est la perte de l’autre joueur, comme par exemple un match de foot PSG et OM.
👉 Si le PSG gagne et l’OM perd, alors on a 1+(-1) = 1-1 = 0
👉 Si le PSG perd et l’OM gagne, alors on a -1+1 = 0
👉 S’il y a match nul, alors on a 0+0 = 0
Le dilemme du prisonnier 🤝
Un braquage a eu lieu. Les policiers décident de convoquer Bonnie et Clyde qui sont présumés complices dans ce braquage. La police n’a pas de preuve pour les inculper de ce braquage, mais assez de preuves pour une peine mineure. Elle décide de les interroger séparément.
Voici les règles du jeu 👇
| Clyde garde le silence | Clyde balance Bonnie | |
| Bonnie garde le silence | Ils prennent 1 an chacun | Clyde libéré et Bonnie fait 10 ans de prison |
| Bonnie balance Clyde | Bonnie libérée et Clyde fait 10 ans de prison | Chacun fait 5 ans de prison |
💡 Le savais-tu ?
Le dilemme du prisonnier est un jeu à somme non nulle car il n’y a pas de compensation de gains. Ce que l’un gagne n’est pas forcément ce que l’autre perd.
Qu’est-ce qu’ils ont intérêt à faire ?
Intuitivement, on se dit qu’ils ont intérêt à se taire tous les deux et faire qu’un an de prison chacun.
Mais voici ce qui peut se passer.
Mets-toi à la place de Bonnie. Voici ce qu’elle se dit :
👉 Si Clyde la balance et qu’elle se tait alors elle fait 10 ans de prison. Elle se dit qu’elle a intérêt à le balancer aussi pour faire 5 ans au lieu de 10 ans.
👉 Si Clyde se tait, elle a intérêt à le balancer pour sortir libre au lieu de faire 1 an de prison.
→ Quel que soit le choix de Clyde, Bonnie a intérêt à le trahir et le balancer.
Et c’est la même chose pour Clyde !
👉 Si Bonnie la balance et qu’il se tait, alors il encourt 10 ans de prison. Il se dit qu’il a intérêt à le balancer aussi pour faire 5 ans au lieu de 10 ans.
👉 Si Bonnie se tait, il a intérêt à la balancer pour sortir libre au lieu de faire 1 an de prison.
→ Il la trahit donc aussi
➡️ Ils vont donc prendre 5 ans de prison chacun !
Tout ça pour dire que même si la bonne solution serait de se taire, si les deux réfléchissent chacun dans leur côté à leur propre intérêt ils vont choisir de trahir. Et ils vont donc se retrouver à faire tous les deux de la prison pendant 5 ans.
Il s’agit de l’équilibre de Nash. Si un joueur décide de changer sa position, il ne peut que perdre. Aucun des joueurs n’a intérêt à bouger s’il est le seul à le faire.
👉 Si Bonnie décide de se taire, alors elle risque 10 ans de prison.
👉 Si Clyde décide de se taire, alors il encourt 10 ans de prison.
La bataille des sexes 🎥
Il s’agit d’un jeu opposant un couple d’une femme et d’un homme qui veulent sortir ce week-end, mais n’ont pas les mêmes envies.
La femme veut aller au théâtre alors que l’homme veut aller au cinéma.
Tu te demandes sûrement pourquoi ils ne vont pas seuls où ils veulent. Eh bien, chacun préfère faire l’activité de son choix plutôt que de participer à l’activité préférée de l’autre, mais ils préfèrent tous les deux passer du temps ensemble plutôt que d’être seuls. Nos deux tourtereaux sont trop amoureux pour laisser l’autre seul.
Voici les règles du jeu 👇
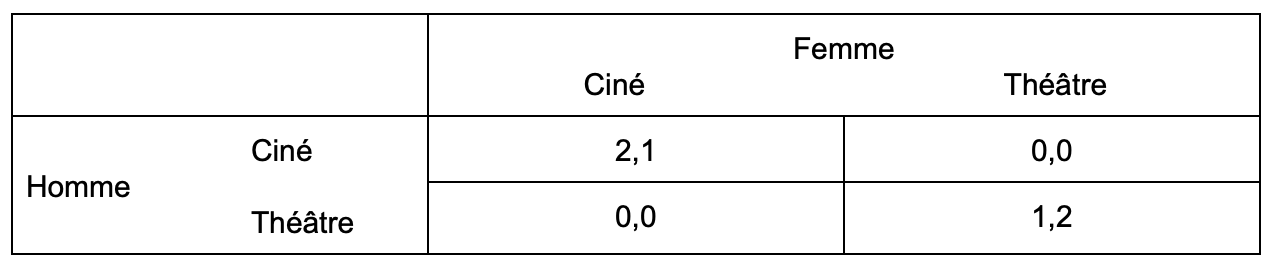
Si les deux vont au cinéma, alors l’homme remporte 2 et la femme 1.
Si les deux vont au théâtre c’est la femme qui remporte 2 et l’homme 1.
S’ils vont séparément ils ne gagnent rien.
Pour ce jeu, il n’y a pas de stratégie optimale. Même s’ils finissent par passer la soirée ensemble, le jeu est déséquilibré car l’un sera plus satisfait que l’autre.
Besoin d’un prof particulier ? ✨
Nos profs sont là pour t’aider à progresser !
La théorie des jeux, à quoi ça sert ? 🧐
Maintenant tu te dis que c’est bien beau de jouer à des jeux, mais ça sert à quoi ? La théorie des jeux sert à prédire et analyser des comportements, élaborer des stratégies, analyser les coopérations et les conflits, prendre des décisions collectives, etc. Elle est présente dans de nombreux domaines ! Voici quelques exemples 👇
En économie 💸
👉 Pour analyser les situations de concurrence, la théorie des jeux permet d’étudier le comportement des entreprises et en ressort les décisions de prix, de publicité ou encore de production.
👉 En théorie des contrats, on l’utilise pour sortir le contrat optimal pour les deux parties.
👉 Durant des enchères, les acheteurs cherchent à faire la meilleure affaire possible en fonction des autres acheteurs. La théorie des jeux permet de modéliser les stratégies, prédire les résultats et déterminer le prix optimal.
Si tu as besoin de cours en économie, n’hésite pas à contacter un de nos Sherpas !
En science politique 👔
👉 La théorie des jeux est utilisée pour analyser les décisions politiques dans le cadre des choix publics. Elle permet de modéliser les comportements des acteurs politiques, les coalitions, les négociations, les compromis et les résultats des processus décisionnels politiques.
👉 Pour des élections, la théorie des jeux est utilisée pour modéliser les interactions entre les partis politiques, les candidats et les électeurs. Elle permet d’analyser les stratégies de campagne, les coalitions, la mobilisation des électeurs et les résultats.
👉 Lors de négociations internationales, la théorie des jeux intervient pour analyser les négociations et les relations internationales entre les pays. Elle permet de comprendre les incitations des dirigeants, les conflits, les accords, et les jeux de pouvoir dans les relations diplomatiques.
💡 Le savais-tu ?
Une des raisons qui a poussé à développer la théorie des jeux est la situation qu’il y avait entre les États-Unis et l’URSS pendant la guerre froide.
| URSS n’investit pas dans l’armement | URSS investit dans l’armement | |
| USA n’investit pas dans l’armement | pas de guerre froide | URSS peut attaquer les USA |
| USA investit dans l’armement | USA peut attaquer l’URSS | guerre froide |
En science sociale 🤝
👉 La théorie des jeux permet d’analyser des situations où les individus doivent prendre des décisions pour coordonner leurs actions. On parle de jeux de coordination comme le dilemme du prisonnier.
👉 La théorie des jeux est utilisée pour analyser les comportements de confiance et de réciprocité.
↪️ Exemple
Un jeu portant sur un ultimatum. Disons que la somme maximum qu’un joueur peut gagner est 100 euros. Si les deux joueurs décident de partager ils remportent chacun 50 euros. Si un joueur décide de partager et l’autre non alors le joueur qui a décidé de ne pas partager remporte 100 euros. Si les deux décident de ne pas partager ils remportent tous les deux 0 euros. Et si les deux ne partagent pas alors ils ne remportent rien non plus. C’est une application du dilemme du prisonnier qu’on développe plus bas dans l’article.
| Joueur 2 partage | Joueur 2 ne partage pas | |
| Joueur 1 partage | 50 chacun | 100 pour le joueur 2 et 0 pour le joueur |
| Joueur 1 ne partage pas | 100 pour le joueur 1 et 0 pour le joueur 2 | 0 chacun |
En biologie 🐻
👉 La théorie des jeux permet d’étudier les interactions entre les prédateurs et leurs proies. On y analyse les comportements d’attaque, de défense des animaux pour maximiser leur chances de survie.
En informatique 💻
👉 Comme pour les enchères en réel, la théorie des jeux est utilisée pour les enchères électroniques. Elle permet de prédire les comportements des acheteurs et donc de maximiser les gains.
👉 En sécurité informatique, la théorie des jeux permet d’analyser le comportement des hackers et donc d’analyser la vulnérabilité d’un système.
Voilà ! Tu connais les bases de la théorie des jeux. N’hésite pas à nous dire en commentaire si cette fiche de cours t’a plu et t’a permis de mieux appréhender cette discipline.
