Le programme de maths de 3ᵉ peut te provoquer quelques cheveux blancs. Pas de panique ! On est là pour démystifier certains chapitres qui peuvent te paraître complexes. Aujourd’hui, on s’attaque à la trigonométrie. On va tout t’expliquer et on te dévoilera même notre formule magique pour ne plus jamais faire l’erreur dans le choix de la formule trigonométrique. (Oui, on est trop cool 😆)
Allez, plus une minute à perdre, let’s go.
La trigonométrie, qu’est-ce que c’est ? 🧐
Définition
La trigonométrie est issue des mathématiques et traite des relations entre angles et distances dans un triangle rectangle. Des fonctions trigonométriques y sont associées comme le cosinus, le sinus et la tangente.
L’objectif de cette discipline est de résoudre des problèmes géométriques.
Les origines de la trigonométrie
La trigonométrie a fait son apparition il y a bien longtemps. Eh oui, on retrouve les premières traces de son utilisation à l’époque égyptienne et babylonienne. Soit 4 000 ans avant l’apparition de l’incontournable Jésus-Christ. Ça fait un bail !
En Europe, on ne redécouvre la trigonométrie qu’à partir de 1595. Légèrement après les Égyptiens. 😅
Cette année-là, le mathématicien Bartholomäus Pitiscus publie un ouvrage intitulé Trigonometria. C’est comme ça que le nom de trigonométrie est né. Le mot est issu du grec, “trigone metron” qui veut dire triangle mesure.

Les métiers qui utilisent la trigonométrie
À l’origine, les Égyptiens utilisaient la trigonométrie pour naviguer et se repérer. Aujourd’hui, elle est toujours employée pour se diriger. Les formules trigonométriques sont aussi employées de nos jours en architecture, ingénierie, astronomie et même en musique.
N’aie donc pas d’inquiétude quant à l’utilité de cette discipline ! 😉

Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Les formules trigonométriques 🧑🏫
La formule trigonométrique du sinus
La fonction sin d’un angle dans un triangle rectangle se définit par le rapport entre la longueur du côté opposé de l’angle et la longueur de l’hypoténuse.
Si tu n’as rien compris avec cette définition, c’est normal. Regarde ce schéma et la formule, ça te semblera plus clair.👇
Formule
sin = dimension du côté opposé / dimension de l’hypoténuse

📌 Rappel : L’hypoténuse correspond au segment opposé à l’angle droit
👉 Exemple :
Le triangle rectangle ABC.
On cherche à calculer le sinus de l’angle C.
Donc :
Sin ( C ) = côté opposé / hypoténuse
Sin ( C ) = 8 / 10
Sin ( C ) = 0,8
Le sin de l’angle C est égal à 0,8.

💡Pour info
Le sinus d’un angle est toujours compris entre 0 et 1. Il n’a pas d’unité de mesure.
La formule trigonométrique du cosinus
La fonction cos d’un angle dans un triangle rectangle se définit par le rapport entre la longueur du côté adjacent de l’angle et la longueur de l’hypoténuse.
Là encore, on te conseille de regarder la formule et le schéma. 👇
Formule
cos = dimension du côté adjacent / dimension de l’hypoténuse

👉 Exemple :
Le triangle rectangle ABC.
On cherche à calculer le cosinus de l’angle C.
Donc :
Cos ( C ) = côté adjacent / Hypoténuse
Cos ( C ) = 6 / 10
Cos ( C ) = 0,6
Le cos de l’angle C est égal à 0,6.

💡 Pour info
Le Cosinus d’un angle est toujours compris entre 0 et 1. Il n’a pas d’unité de mesure.
La formule trigonométrique de la tangente
La fonction tan d’un angle dans un triangle rectangle se définit par le rapport entre la longueur du côté opposé de l’angle et la longueur du côté adjacent de l’angle.
Même chose, regarde 👇 pour mieux comprendre.
Formule
tan = dimension du côté opposé / dimension du côté adjacent

👉 Exemple :
Le triangle rectangle ABC.
On cherche à calculer la tangente de l’angle C.
Donc :
Tan ( C ) = côté opposé / côté adjacent
Tan ( C ) = 8 / 6
Tan ( C ) = 1,3
La tan de l’angle C est égale à 1,3

💡 Pour info
La tangente peut être supérieure à 1. Elle n’a pas d’unité de mesure.
À lire aussi
Révise tes cours de maths en revoyant le théorème de Thalès.
La formule magique des Sherpas ✨
C’est le moment de te révéler notre secret pour que tu évites de te prendre la tête avec ces trois fonctions.
SOH CAH TOA
Ce petit mot t’aidera à ne pas te mélanger les pinceaux. On t’explique pourquoi.
- Le premier groupe de mots SOH représente la formule du sinus. La première lettre S représente le sinus. Le O représente le côté opposé et le H représente l’hypoténuse.
- Le deuxième groupe de mots CAH représente la formule du cosinus. La première lettre C représente le Cosinus. La seconde lettre A représente le côté adjacent et le H représente l’hypoténuse.
- Le troisième groupe de mots TOA représente la formule de la tangente. La première lettre T représente la tangente. La seconde lettre O représente le côté opposé et le A représente le côté adjacent.
Avec cette technique, tu es sûr de ne plus te tromper et tu sais aussi dans quel ordre placer les valeurs. Tu n’auras qu’à suivre l’ordre d’écriture de SOH CAH TOA. On te conseille de l’apprendre par cœur ! 💖
À lire aussi
Les exercices 📝
C’est le moment de te mettre à l’épreuve. On vérifie ensemble que tu as bien compris le cours. 😊
Exercice 1 :
Utilise la formule trigonométrique qui convient pour trouver le cos, le sin et la tan des angles B et C.

Exercice 2 :
Utilise le cosinus de B pour retrouver la mesure de l’hypoténuse.

Exercice 3 :
Utilise le sinus de B pour retrouver la mesure du côté opposé de l’angle B.

Les corrections ✅
Exercice 1 :
Pour l’angle B :
- Cos (B) = côté adjacent / hypoténuse =
16 / 20 = 0,8.
Le cos de B est égal à 0,8. - Sin (B) = côté opposé / hypoténuse =
13 / 20 = 0,65.
Le sin de B est égal à 0,65. - Tan (B) = côté opposé / côté adjacent =
13 / 16 = 0,81.
La tan de B est égale à 0,81.
Pour l’angle C :
- Cos ( C ) = côté adjacent / hypoténuse =
13 / 20 = 0,65.
Le cos de C est égal à 0,65. - Sin ( C ) = côté opposé / hypoténuse =
16 / 20 = 0,8.
Le sin de C est égal à 0,8. - Tan ( C ) = côté opposé / côté adjacent =
16 / 13 = 1,23.
La tan de C est égale à 1,23.
Exercice 2 :
En 3ᵉ, tu seras amené à utiliser le cosinus ou le sinus d’un angle pour retrouver la mesure d’un segment qui compose l’angle. Pour cela, tu devras utiliser le produit en croix.
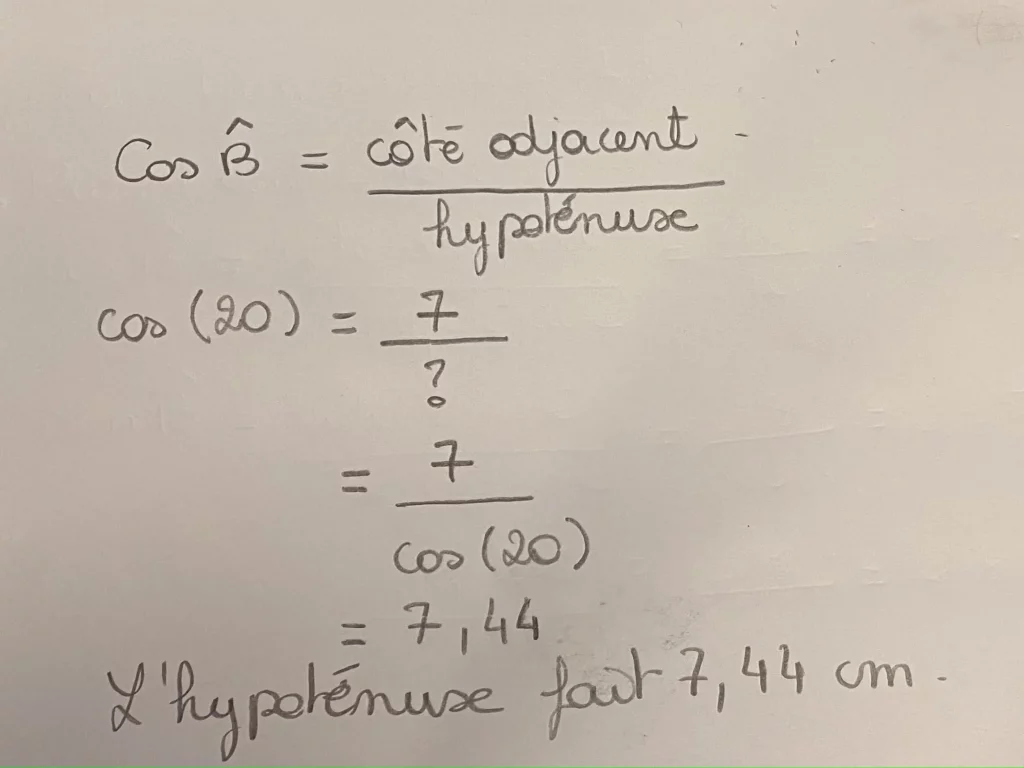
📌 Rappel du produit en croix :

Exercice 3 :
Ici aussi, tu devras utiliser le sinus d’un angle et le produit en croix, pour retrouver la mesure d’un segment qui le compose. On te met la correction juste en dessous.

Ton premier cours particulier de maths est offert ! 🎁
Tous nos profs sont passés par les meilleures écoles de France !
Le tableau des formules trigonométriques
On s’est dit que cela pourrait te faciliter la vie d’avoir un tableau qui résume les formules. 😆 N’hésite pas à le recopier !
| Nom de la formule | Éléments concernés | Formule |
|---|---|---|
| Sinus | - le côté opposé - l'hypoténuse | sin = côté opposé / hypoténuse |
| Cosinus | - le côté adjacent - l'hypoténuse | cos = côté adjacent / hypoténuse |
| Tangente | - le côté opposé - le côté adjacent | tan = côté opposé / côté adjacent |
Progresser rapidement 📈
On te présente trois de nos conseils pour progresser rapidement en trigonométrie.
- Apprendre les formules trigonométriques par cœur 💖 : c’est l’étape la plus importante du chapitre. Grâce à ça tu seras incollable sur le sujet. Pour t’aider dans cette démarche, n’hésite pas à utiliser SOH CAH TOA !
- Faire des exercices : en mathématiques, il est important de mettre en pratique la leçon. N’hésite pas à faire des exercices pour vérifier tes acquis. C’est la meilleure façon de progresser. Parole de Sherpas ! 🤚
- Prends des cours particuliers : si tu as toujours des difficultés, n’hésite pas à prendre des cours particuliers de maths. Cela peut vraiment t’aider dans ta progression. De plus, nos Sherpas sont les meilleurs du milieu, tu trouveras forcément celui qui saura répondre à tes besoins.
Après avoir lu cet article, la trigonométrie et ses formules ne devraient plus avoir aucun secret pour toi. 😆
N’oublie pas, pense SOH CAH TOA et tu trouveras forcément la solution. On espère que cet article a pu t’aider et si oui, n’hésite pas à nous le dire en commentaires !