Lorsque tu réalises une figure géométrique, il peut arriver que tu doives changer les dimensions en l’agrandissant ou en la rétrécissant pour plus de lisibilité. Dans ce cas, il est essentiel de garder les mêmes proportions ! C’est là que notre amie l’homothétie rentre en jeu !
Aujourd’hui, on te parle de cette transformation géométrique essentielle utilisée dans de nombreux domaines ! 🚀
Qu’est-ce que l’homothétie ? 🤔
Définition
L’homothétie est une transformation géométrique qui consiste à agrandir ou à réduire une figure en conservant ses proportions. Elle est souvent utilisée en mathématiques et en géométrie pour représenter des objets de manière similaire, mais de tailles différentes !
L’homothétie préserve certaines propriétés géométriques, telles que les angles. Elle est surtout utilisée dans de nombreux domaines, tels que l’art, l’architecture, la cartographie ou le graphisme 😍 !
Le centre d’homothétie 🎯
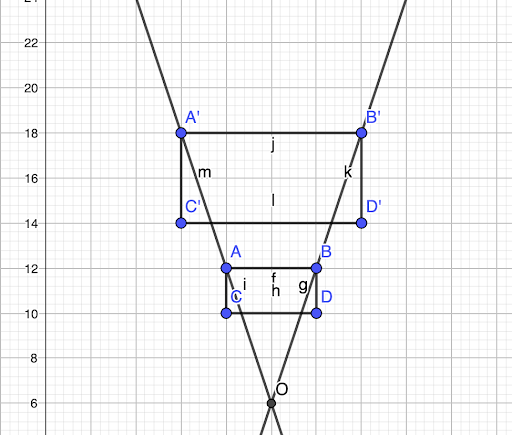
Le centre d’homothétie (O) est le point autour duquel une figure géométrique subit une homothétie ! Il reste fixe et ne change pas de position après la transformation !
📌 Pour le trouver, il te suffit de :
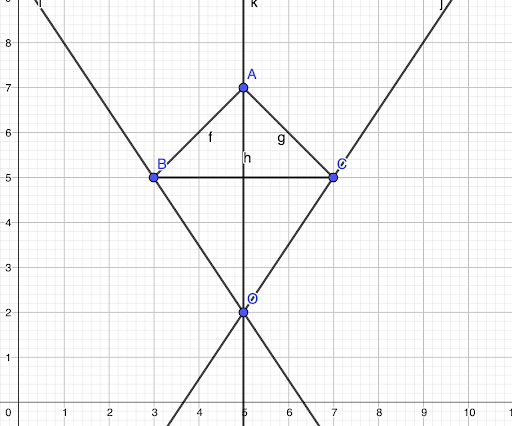
👉 Tracer une droite qui passe par les sommets A et A’,
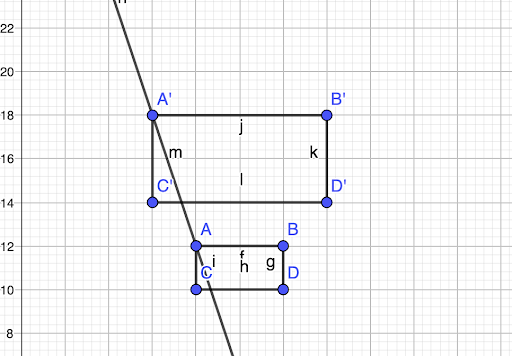
👉 Tracer une droite qui passe par les sommets B et B’.
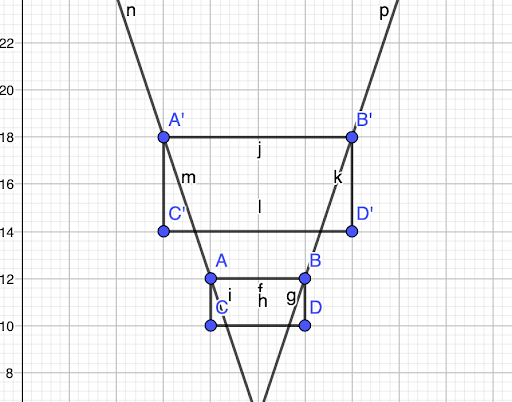
Eh voilà, le centre d’homothétie est le point d’intersection des deux droites tracées précédemment (O) 👇
Ton premier cours particulier est offert ! 🎁
Nos profs sont passés par les meilleures écoles et universités.
Rapport d’homothétie 🧐
Explication
📌 Le rapport d’homothétie est le rapport de proportionnalité entre deux figures après une homothétie !
📌 Par exemple, si un rapport d’homothétie est égal à 2, cela signifie que la figure est deux fois plus grande que la première. A contrario, s’il est égal à 0,5, la figure est deux fois plus petite 😉.
📌 Il est noté par la variable k et peut aussi être appelé rapport de similitude !
Influence de sa valeur
Le rapport d’homothétie influence la taille de la figure, mais pas seulement ! Il influence aussi son sens dans certains cas. 👇
Influence de sa valeur sur la taille
👉 Lorsque k > 1, ça signifie que la figure aura des dimensions plus grandes que l’originelle. Par exemple, si k = 2, la figure sera deux fois plus grande que l’originelle.
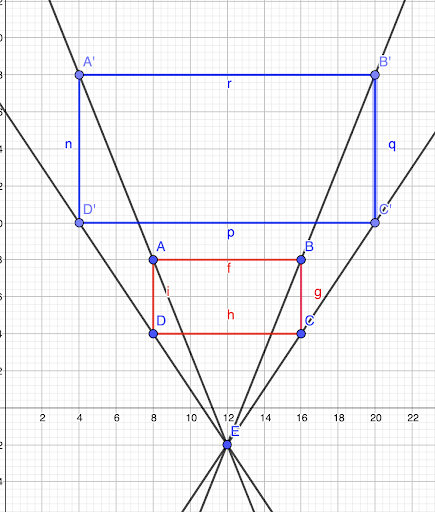
👉 Lorsque 0 < k < 1, ça signifie que la figure aura des dimensions plus petites que l’originelle.
Par exemple, si k = 0,5, la figure sera deux fois plus petite que l’originelle.
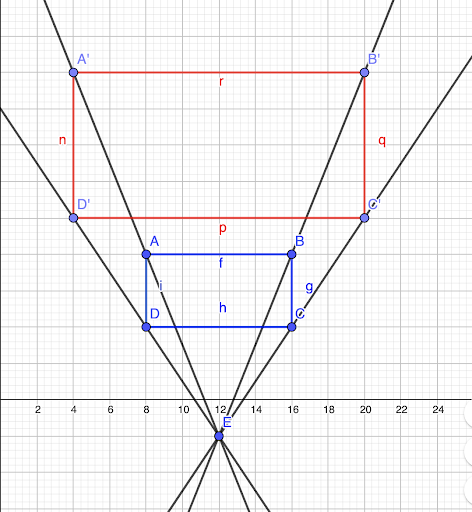
👉 Lorsque k = 1, ça signifie que la figure aura exactement les mêmes proportions que l’originelle.
Influence de sa valeur sur le sens
Le sens de la figure va uniquement changer lorsque k < 0. Dans ce cas, le centre d’homothétie O devient comme un axe de symétrie, et la figure change de sens comme si elle était face à un miroir !
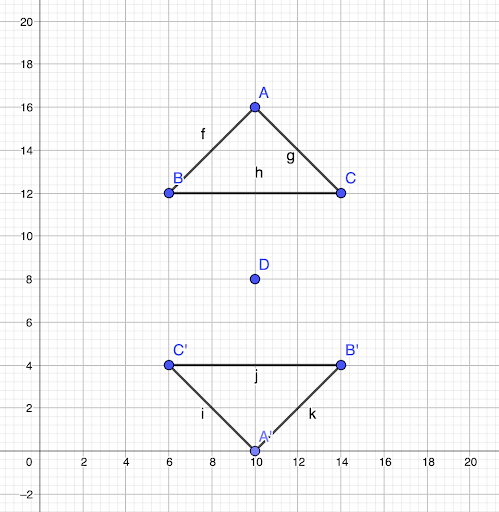
k = -1
À lire aussi
Découvre avec nous un des solides phares de la géométrie : le tétraèdre ! 🔺
Calculer le rapport d’homothétie
Pour calculer le rapport d’homothétie ou rapport de proportionnalité entre les deux figures, il suffit d’utiliser la formule suivante 👇
k = Distance entre le centre d’homothétie et le sommet de l’image / Distance entre le centre d’homothétie et le sommet initial
La construction d’une figure par homothétie 📐
On arrive sur la partie un peu plus délicate de cette notion : la construction de l’image 😬. Pas de panique, on t’explique ça étape par étape ! 👇 !
👉 Prenons par exemple cette figure avec un rapport d’homothétie noté k=2
- Trace une droite reliant chaque sommet au centre d’homothétie
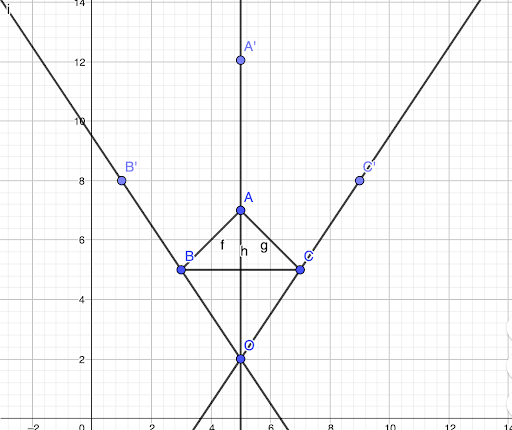
- Tu vas ensuite mesurer chaque distance entre les sommets et le centre d’homothétie, puis multiplier ces distances par le rapport d’homothétie. Ces calculs vont te permettre de trouver la distance séparant les sommets de l’image avec le centre d’homothétie !
- Tu reportes ensuite ces mesures sur les droites que tu as précédemment tracées ! Par exemple, pour reporter A’, tu mesures 10 cm sur ta droite passant par A, en partant de O !
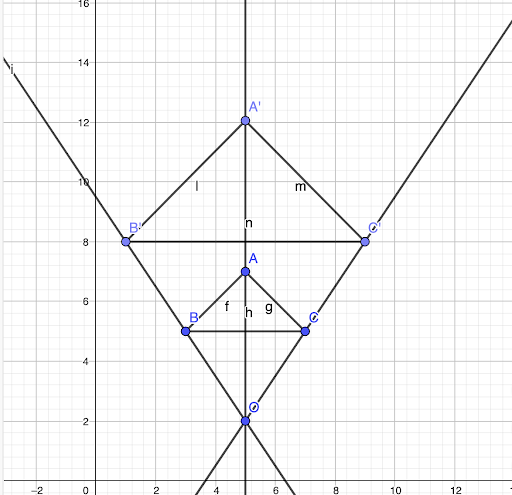
- Pour finir, il te suffit de relier les points, pour tracer ta figure 🥳
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Exercices ✍️
Trouve le centre d’homothétie de cette figure
Correction :
👉 Trace une droite reliant B et B’
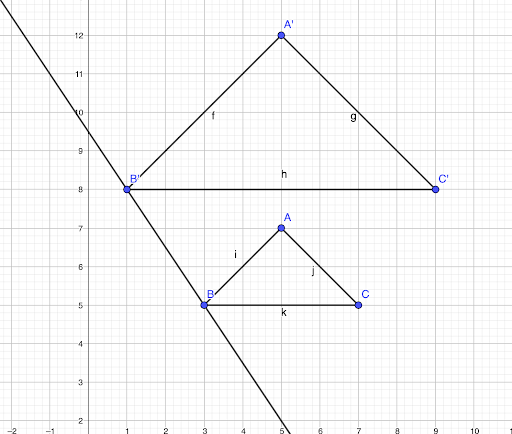
👉 Trace une droite reliant C et C’
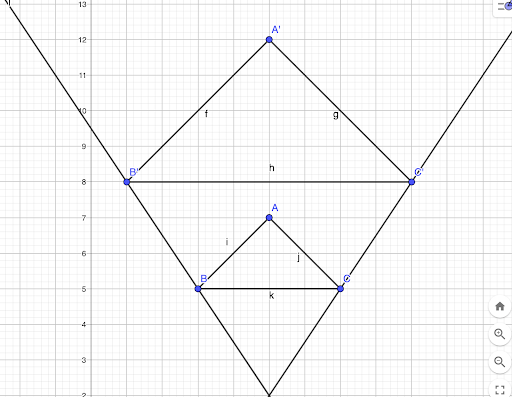
👉 Le centre d’homothétie est le point d’intersection des deux droites tracées préalablement (O) !
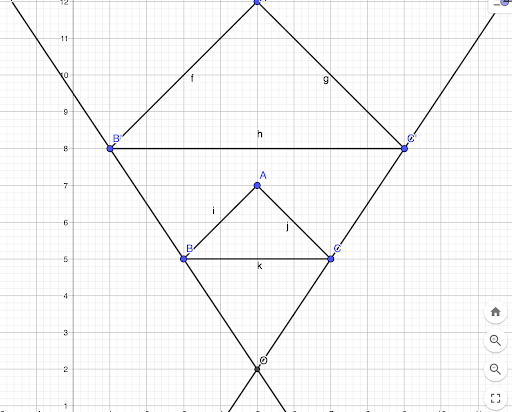
Calcule le rapport d’homothétie de cette figure
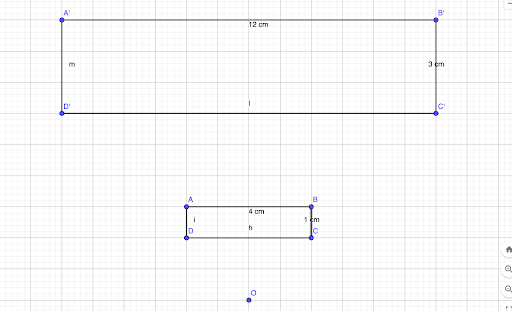
Correction :
Pour calculer le rapport d’homothétie, il nous faut calculer les distances OA et OA’
On a donc un rapport d’homothétie de 3, c’est-à-dire que l’image est trois fois plus grande que la figure originelle.
💡 Pour info
On aurait peu utilisé OC et OC’ ainsi qu’OB et OB’ 😉
Voilà maintenant, tu sais tout sur l’homothétie et tu es capable de reproduire une figure avec précision peu importe sa taille ! Si tu as besoin de plus d’aide en maths, n’hésite pas à contacter l’un de nos Sherpas pour prendre des cours particuliers de maths en ligne !

FAQ ✅
Comment définir une homothétie?
L’homothétie est une transformation géométrique qui agrandit ou réduit une figure par rapport à un point fixe, appelé le centre d’homothétie. Elle conserve les formes mais modifie les tailles.
Comment calcule-t-on une homothétie?
Pour effectuer une homothétie, on multiplie la distance entre chaque point de la figure et le centre d’homothétie par le rapport d’homothétie. Ceci donne les nouveaux emplacements des points.
Quelles sont les propriétés d’une homothétie?
L’homothétie conserve les angles, les parallélismes et les alignements. Toutefois, elle modifie les longueurs selon le rapport d’homothétie choisi.