Pendant toute ta scolarité, tu vas entendre parler d’abscisse et d’ordonnée. Eh oui, ces notions sont utilisées principalement en mathématiques, mais pas que. Tu les retrouves aussi dans d’autres matières scientifiques ! Tu l’as compris, il est essentiel que tu les maîtrises sur les bouts des doigts ! Alors découvre avec nous, ce que c’est et comment les utiliser !
Repère cartésien 💫
Avant de parler des coordonnées, il est important de comprendre la définition d’un repère cartésien 👇.
Un repère cartésien est un système de référence qui permet de localiser et d’identifier des points dans un plan. Il se compose de deux axes : l’axe horizontal (ou axe des abscisses) et l’axe vertical (ou axe des ordonnées). Ces deux axes se croisent en un point appelé l’origine du repère !
L’abscisse 📍
L’abscisse est la coordonnée horizontale d’un point dans un repère cartésien ou sur une droite graduée. Elle indique la distance entre ce point et l’axe vertical. Pour représenter l’abscisse d’un point, on utilise généralement la lettre « x ».
Par exemple, si tu as un point P avec une abscisse de 5, cela signifie que P est situé à cinq unités à droite de l’origine.
L’ordonnée 📍
L’ordonnée est la coordonnée verticale d’un point dans un repère cartésien. Elle indique la distance entre ce point et l’axe horizontal. Pour représenter l’ordonnée d’un point, on utilise généralement la lettre « y ».
Par exemple, si tu as un point Q avec une ordonnée de 2, cela signifie que Q est situé à deux unités au-dessus de l’origine.
Se repérer dans un plan 🧭
Maintenant que tu as compris ce que sont l’abscisse et l’ordonnée, tu peux facilement lire les coordonnées d’un point ! Elles sont généralement écrites sous la forme (x, y), avec x l’abscisse et y pour l’ordonnée !
Donc si tu as un point R avec des coordonnées (4, 1), cela signifie que R est situé à quatre unités à droite de l’origine et une unité au-dessus de l’origine.

💡 Pour info
Les coordonnées peuvent très bien être négatives !
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Dans quel domaine utilise-t-on cette notion ? 🤔
Géométrie 📏
Les coordonnées des points dans un repère cartésien sont énormément utilisées en géométrie.
Tu seras amené à tracer des figures géométriques telles que des segments, des droites ou des polygones dans un plan ! En utilisant les coordonnées des points, tu peux déterminer les longueurs, les aires et les périmètres de ces figures. Les coordonnées te permettront également de démontrer des propriétés géométriques en utilisant des calculs précis.
Algèbre 🔢
En algèbre, les coordonnées des points sont essentielles pour résoudre des équations et des systèmes d’équations. Tu peux représenter graphiquement les équations linéaires en utilisant les coordonnées de leurs points solutions. Ça peut t’aider à comprendre visuellement les relations entre les variables et à résoudre certains problèmes d’équations plus facilement !
Physique 👨🏻🔬
En physique, tu vas souvent utiliser des graphiques pour représenter des phénomènes et des relations mathématiques. Les coordonnées des points dans un repère cartésien te permettront de tracer des graphiques de vitesses, de forces, de mouvements, etc. Notamment quand tu verras la 3ᵉ loi de Newton !

Fonction 📊
Eh oui, tu vas en manger des fonctions dans ta scolarité, alors connaître son repère cartésien, c’est très très TRÈS important pour bien maîtriser cette notion et ce pour plusieurs raisons 👇.
👉 Représentation graphique
Les fonctions peuvent être représentées sous forme de courbes dans un plan cartésien. L’abscisse correspond généralement à une variable indépendante, souvent notée « x », tandis que l’ordonnée correspond à la variable dépendante, souvent notée « y ». En utilisant les coordonnées des points, tu peux tracer la courbe représentative d’une fonction et ainsi visualiser son comportement global !
👉 Lecture des coordonnées
En connaissant l’abscisse d’un point, tu peux facilement trouver l’ordonnée correspondante et vice versa. Cette compétence est essentielle pour comprendre les valeurs associées à différents points de la fonction, telles que les extrema, les intersections avec les axes, les valeurs spécifiques, etc !
👉 Analyse des variations
En étudiant les coordonnées des points sur la courbe d’une fonction, tu peux analyser les variations d’une fonction ! Tu peux alors déterminer les intervalles dans lesquels la fonction est croissante, décroissante, constante, etc !
À lire aussi
Trouver l’équation d’une droite 🔎
Voici les 5 étapes pour trouver l’équation d’une droite à l’aide des coordonnées de deux points 👇 :
1️⃣ Détermine la valeur de la pente :
Pour calculer la pente (m) d’une droite à partir de deux points donnés (x1, y1) et (x2, y2), utilise la formule suivante :
2️⃣ Remplace la pente dans l’équation D
Dans l’équation de la droite :
Remplace le paramètre m par la valeur de la pente que tu as calculée à l’étape 1.
3️⃣ Remplace les coordonnées d’un des points
Choisis l’un des deux points donnés (x, y) et remplace x et y dans l’équation par les valeurs correspondantes du point choisi.
4️⃣ Isole le paramètre
Isole le paramètre en résolvant l’équation.
5️⃣ Écris l’équation de la droite
Maintenant que tu as la valeur de la pente (m) et du paramètre d’ordonnée à l’origine (b), écris l’équation de la droite sous la forme :
En utilisant les valeurs des paramètres m et b que tu as obtenues !
À lire aussi
Découvre avec nous l’un des solides phares de la géométrie : le tétraèdre !
Besoin d’un prof particulier ? ✨
Nos profs sont là pour t’aider à progresser !
Exercices ✍️
Trouve les coordonnées de ces points 🔎 :
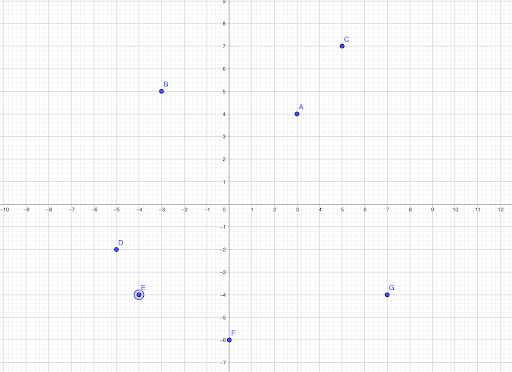
Correction :
A (3;4)
B (-3;5)
C(5;7)
D(-5;-2)
E(-4;-4)
F(0;-6)
G(7;-4)
Trouve l’équation de cette droite 🔎 :
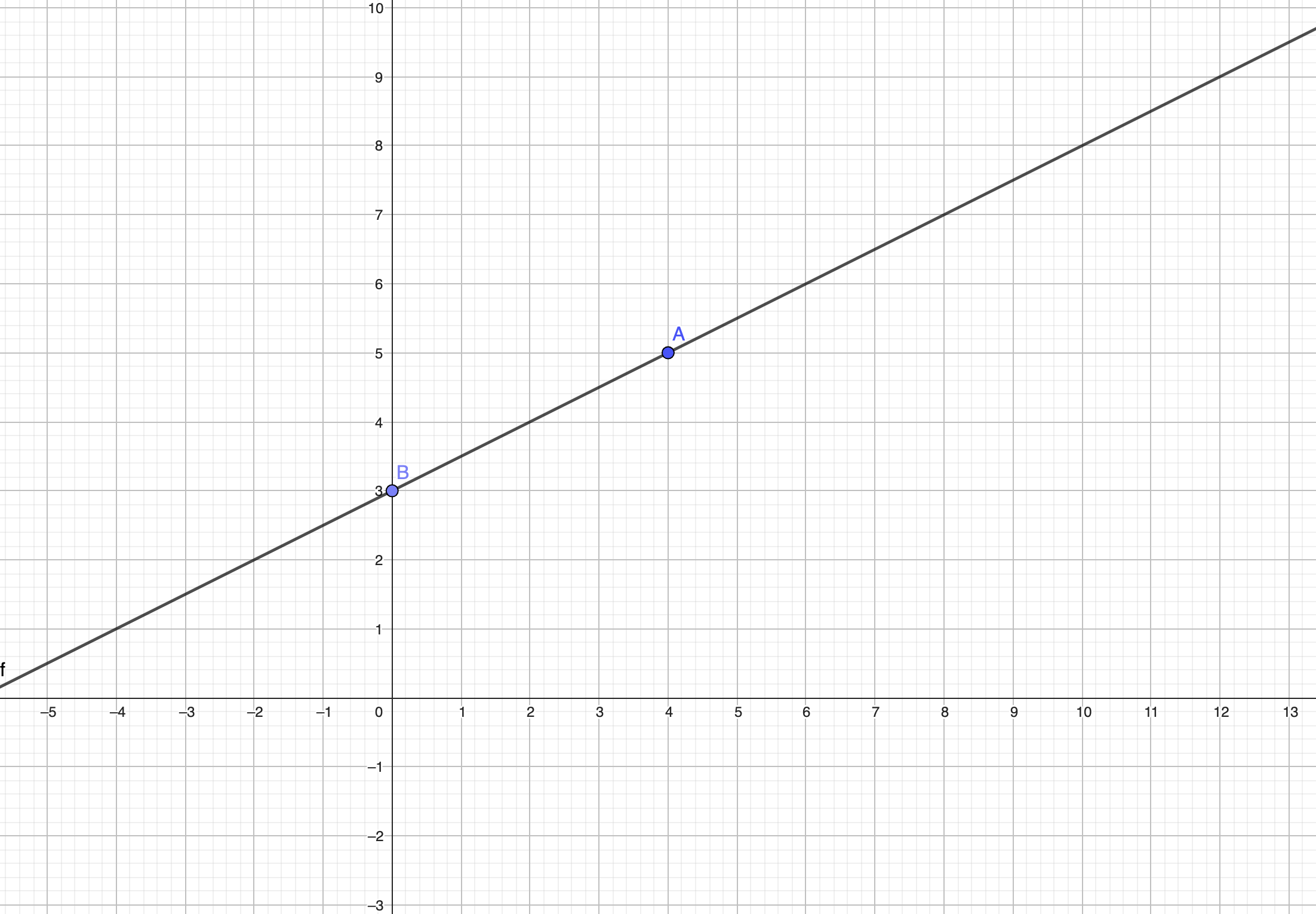
Correction :
1️⃣ Détermine la valeur de la pente
On utilise les coordonnées des points A et B
2️⃣ Remplace la pente dans l’équation D
Remplace le paramètre m par la valeur de la pente
3️⃣ Remplace par les coordonnées d’un des points
On utilise les coordonnées du point A
4️⃣ Isole le paramètre
5️⃣ Écris l’équation de la droite
Eh voilà, maintenant que tu sais te repérer comme un chef dans un repère cartésien, tu vas pouvoir être à l’aise dans pas mal de matière ! Si tu as besoin de plus d’aide, n’hésite pas à contacter un de nos professeurs en mathématiques en ligne 😉 !













