🔢 Probabilités {fiche de maths}

Tu souhaites calculer tes chances de réussir ton prochain contrôle de maths ? Eh bien, sache qu’avec cette fiche de cours, ta note risque de bien augmenter. Aujourd’hui, on t’apprend les bases d’un thème clé en mathématiques : les probabilités ! Tu es prêt ? C’est parti !

Quand tu calcules des probabilités ! — *Quand tu calcules ta probabilité de réussir ton année sans les Sherpas !*

Les probabilités, c’est quoi ? 👀

Définition 📖

Les probabilités sont une branche des mathématiques qui étudient les phénomènes aléatoires.

Ce sont les chances qu’un événement se produise.

Notions à connaître 📜

Quand tu prends des notes sur les probas ! — *Prends des notes !*

📌 Expérience aléatoire : expérience qui dépend du hasard, mais dont les résultats possibles sont connus.

↪️ Exemple : lancer un dé non pipé

📌 L’univers ou l’espace des possibles : l’ensemble de tous les résultats possibles d’une expérience aléatoire.

Il est noté $\Omega$ .

↪️ Exemple : si on garde l’exemple du lancer de dé non pipé, l’espace des possibles est :

$\Omega={1, 2, 3, 4, 5, 6}$

📌 Événement : un sous-ensemble de l’espace des possibles. On le note par une lettre majuscule.

↪️ Exemple : toujours avec notre lancer de dé, l’événement A est “obtenir un nombre impair”

A={1, 3, 5}

👉 Événement élémentaire : une seule issue

👉 Événement impossible : irréalisable

👉 Événement certain : toutes les issues

👉 Événement contraire de A : tout sauf l’événement A

📌 Nombre d’éléments dans un événement : on note card de l’événement.

↪️ Exemple : encore et toujours avec notre lancer de dé, l’événement A est “obtenir un nombre impair”

A={1, 3, 5} → l’événement A contient 3 éléments donc card(A)=3

📌 L’événement $A\cup{B}$ ou A union B : la réalisation de A ou de B ou des deux simultanément.

📌 L’événement $A\cap{B}$ ou A inter B : la réalisation de A et de B

Propriétés 🤔

La probabilité d’un événement A, noté P(A), est la somme des probabilités des évènements qui le composent → $0\leq{P(A)}\leq1$

Un événement certain a une probabilité qui vaut 1 → $P(\Omega)=1$

Un événement impossible a une probabilité qui vaut 0 → $P(\phi)=0$

Formules 🤓

$P(A)=\frac{cardA)}{card(\Omega)}$

$P(A\cap{B})=P(A)\timesP_A(B)$

$P(A\cup{B})=P(A)+P(B)$

$P(A\cup{B})=P(A)+P(B)-P(A\cap{B})$ si A et B sont possibles

$P_A(B)=\frac{P(A\cap{B})}{P(A)}$

$P(\bar{A})=1-P(A)$

$P(A)=P(A\cap{B})+P(A\cap{\bar{B}})$

Probabilités conditionnelles et indépendance 🧐

La probabilité conditionnelle de l’événement A sachant l’événement B, notée P(A|B) ou $P_{A}(B)$ , représente la probabilité que A se produise sachant que B s’est déjà produit.

$P_{A}(B)=\frac{P(A\cap{B})}{P(A)}$

Les événements A et B sont indépendants si et seulement si :

$P(A\cap{B})=P(A)\times{P(B)}$

et donc :

$P_{A}(B)=P(A)$

Pour savoir si les événements A et B sont indépendants, il faut calculer $P(A\cap{B})$ et $P(A)\times{P(B)}$ .

S’ ils sont égaux alors ils sont indépendants. S’ils sont différents, alors ils sont dépendants.

Quand des événements sont indépendants ! — *Quand l’événement A n’a pas besoin de l’événement B !*

Variable aléatoire et loi de probabilité 🤔

Une variable aléatoire est une application X de $\Omega$ . C’est un peu abstrait, mais avec une application concrète, tu vas mieux comprendre.

💡 Le savais-tu ?

Une variable aléatoire est dite “discrète” quand l’ensemble des valeurs qu’elle peut prendre est fini ou dénombrable.

Exemples :

Un lancer de dé car il ne peut prendre que 6 valeurs : 1, 2, 3, 4, 5, 6.

Pile ou face car il ne peut prendre que 2 valeurs : pile, face.

Tu lances un dé, si tu tombes sur 1 ou 2 tu perds 2 points, si tu tombes sur 3 ou 4, tu as 0 points et si tu tombes sur 5 ou 6, tu gagnes 5 points.

Quand tu calcules ta probabilité d'avoir un deux 6 !

On peut alors définir une loi de probabilité, c’est-à-dire la probabilité d’obtenir chacune des valeurs de X que l’on note $x_i$ . Ici on a $x_1$ , $x_2$ et $x_3$

$P(X=x_1)$ est la probabilité d’obtenir 1 ou 2 au lancer de dé

$P(X=x_2)$ est la probabilité d’obtenir 3 ou 4 au lancer de dé

$P(X=x_3)$ est la probabilité d’obtenir 5 ou 6 au lancer de dé

$P(X=x_1)=P(X=-2)=P({1;2})=\frac{2}{6}=\frac{1}{3}$

$P(X=x_2)=P(X=0)=P(3;4})=\frac{2}{6}=\frac{1}{3}$

$P(X=x_3)=P(X=5)=P({5;6})=\frac{2}{6}=\frac{1}{3}$

Pour résumer :

Si tu as besoin d’aide, n’hésite pas à prendre des cours de probabilités avec un de nos Sherpas !

Exercices ✍️

Maintenant, place à la pratique !

Exercice 1

Tu tires au hasard dans un paquet de 52 cartes.

Calcule la probabilité d’avoir un roi.
Calcule la probabilité d’avoir la dame de cœur ou le 7 de pique.

Exercice 2

Tu vas au restaurant.

Tu as 60% de chance de choisir le burger et 40% de choisir la salade. On note P(B) la probabilité de choisir le burger et P(S) la probabilité de choisir la salade.

Si tu choisis le burger, tu as 20% de chance de prendre un dessert.

Si tu choisis la salade, tu as 90% de chance de prendre un dessert.

On note P(D) la probabilité de prendre un dessert.

La probabilité de prendre un burger et un dessert sont-ils indépendants ?
Calcule la probabilité de prendre une salade et pas de dessert.

Ta probabilité de prendre un burger ! — *Sa-QUOI?*

Exercice 3

On lance 2 fois une pièce de monnaie. On désigne X comme étant la variable aléatoire représentant le nombre de face obtenus. Détermine la loi de probabilité de X.

Corrections 💯

Correction 1

1. Si tu as déjà joué aux cartes, tu sais que dans un jeu, il y a 4 rois (le roi de cœur, le roi de carreau, le roi de pique et le roi de trèfle).

On note P(A) la probabilité de tirer un roi.

La formule est : $P(A)=\frac{card{A}}{card{\Omega}}$

$P(A)=\frac{4}{52}=\frac{1}{13}$

Tu as donc une chance sur 13 de tomber sur un roi.

2. Il y a une dame de cœur et un 7 de pique dans un jeu de cartes.

On note P(B) la probabilité de tirer la dame de cœur et P(C) la probabilité de tirer le 7 de pique. On applique la formule suivante :

P(B\cup{C})=P(B)+P(C)

⚠️ Attention ! Vu que tu tires une seule carte, B et C ensemble ne sont pas possible. Si tu avais tiré deux cartes simultanément tu aurais choisi la formule suivante : $P(B\cup{C})=P(B)+P(C)-P(B\cap{C})$

$P(B)=\frac{1}{52}$

$P(C)=\frac{1}{52}$

$P(B\cup{C})=\frac{1}{52}+\frac{1}{52}=\frac{2}{52}=\frac{1}{26}$

Ta probabilité d'avoir un As de carreau ! — *On ne l’avait pas prévue celle-là !*

Correction 2

Pour cet exercice, le mieux est de te faire un arbre pour bien visualiser les probabilités.

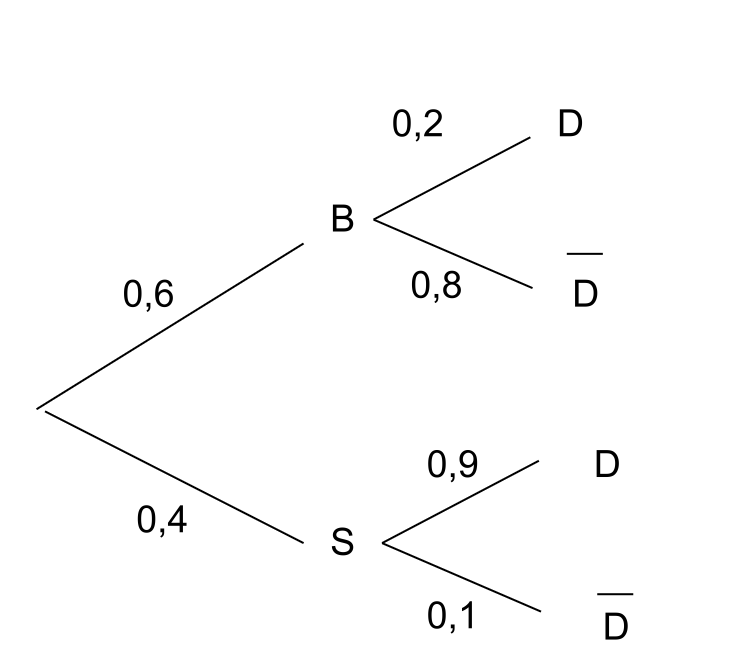
On sait que si les événements B et D sont indépendants alors :

$P(B\cap{D})=P(B)\timesP(D)$

Tu dois alors calculer $P(B\cap{D})$ et $P(B)\timesP(D)$ séparément

$P(B\cap{D})=0,6\times0,2=0,12$

$P(B)=0,6$

$P(D)=0,6\times0,2+0,4\times0,9=0,48$

$P(B)\times{P(D)}=0,6\times0,48=0,288$

$P(B\cap{D})\neq{P(B)\times{P(D)}}$

Les événements B et D sont donc dépendants.

2. Calcul de la probabilité de prendre une salade et pas de dessert.

On note $P(S)$ la probabilité de prendre une salade, $P(\bar{D})$ la probabilité de ne pas prendre de dessert et $P_S{(\bar{D})}$ la probabilité de ne pas prendre de dessert sachant qu’on a pris une salade. On applique la formule suivante :

$P(S\cap{\bar{D}})=P(S)\times{P_S(\bar{D})}$

$P(S\cap{\bar{D}})=0,4\times0,1=0,04$

Correction 3

On note $X(\Omega)$ comme étant l’ensemble des valeurs que peut prendre la variable aléatoire X. On note F l’événement “obtenir face” et P l’événement “obtenir pile”.

Tu lances 2 fois le dé. Tu peux avoir FF, PP, PF, FP. L’ensemble des possibles est donc $\Omega={FF, PP, PF, FP}$

Donc tu peux avoir 2 fois face, 1 fois face et aucune fois face.

$X(\Omega)={0,1,2}$

On définit la loi de probabilité de X :

$P(X=x_1)=P(X=0)=\frac{1}{4}$

$P(X=x_2)=P(X=1)=\frac{2}{4}=\frac{1}{2}$

$P(X=x_3)=P(X=2)=\frac{1}{4}$

On peut résumer la loi de probabilité de la variable aléatoire X comme ceci :

On arrive au bout de notre fiche de mathématiques sur les probabilités. On espère qu’elle t’a plu et t’a aidé à mieux comprendre comment les appliquer. Si tu as quelques difficultés, n’hésite pas à prendre des cours de maths avec un de nos Sherpas !