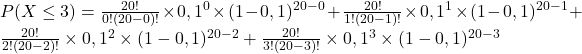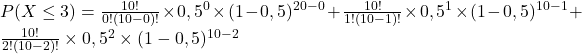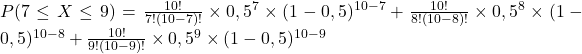🔢 Loi binomiale {fiche de maths}

Aujourd’hui, on te parle d’une notion clé en probabilités : la loi binomiale ! Dans cette fiche de cours on t’explique ce qu’est cette loi de probabilité et comment l’appliquer dans des exercices. Tu es prêt ? C’est parti ! 🚀

You ARE a math guy — *Toi, avant de connaître les Sherpas !*

La loi binomiale, c’est quoi ? 👀

Histoire 📚

L’histoire de la loi binomiale remonte à l’année 1713 avec Jacob Bernoulli, un mathématicien suisse.

Jacob Bernoulli étudie les processus de tirage aléatoire, notamment les jeux de pile ou face. Il réalise des expériences et observe les résultats obtenus. Il formule ensuite des principes mathématiques pour décrire ces résultats.

Il introduit la loi binomiale formellement dans son ouvrage Ars Conjectandi. Lors d’une même expérience, indépendante, répétée plusieurs fois qui admet deux issues (le succès ou l’échec), Bernoulli utilise la loi binomiale pour modéliser le nombre de succès.

Aujourd’hui, la loi binomiale est un des concepts fondamentaux de la théorie des probabilités !

Définition 📖

Si tu as lu l’histoire de la binomiale, tu l’as bien compris, elle a un rapport avec la loi de Bernouilli. On t’explique !

💡 Rappel de la loi de Bernoulli

Soit une épreuve de Bernoulli de paramètre p et X une variable aléatoire discrète qui vaut 1 si l’épreuve donne un succès et 0 si elle donne un échec.
P(X= 1) = p et P(X=0) = 1- p, avec 0 ≤ p ≤ 1

La loi binomiale, de paramètres n et p, est la loi de probabilité d’une variable aléatoire X égale au nombre de succès rencontrés au cours d’une répétition de n épreuves de Bernoulli, p étant la probabilité de succès dans chacune d’entre elles.

On note :

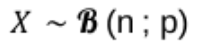
Donc la loi binomiale est une loi de Bernoulli, mais avec plusieurs épreuves qui ne dépendent pas les unes des autres.

Formule 🤓

$P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}$

$P(X=k)=\frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}$

La combinaison $\binom{n}{k}$ est le coefficient de binomiale. On dit aussi k parmi n, donc les succès parmi toutes épreuves.

n : paramètre du nombre d’épreuves de Bernoulli
p : paramètre de la probabilité d’avoir un succès
(1-p) : la probabilité d’avoir un échec
k : le nombre de succès

💡 Rappel sur les

n!=1x2x3x…x(n-1)xn

↪️ Exemple

4!=1x2x3x4=24

Propriétés

L’espérance de X, notée E(X), est la moyenne des valeurs possibles de X pondérée par les probabilités que ces valeurs arrivent.

👉 E(X)=np

La variance de X, notée V(X), est l’écart moyen entre chaque valeur et la moyenne. Elle permet de voir si les différentes valeurs sont plus ou moins dispersées.

👉 V(X)=np(1-p)

Si tu as des lacunes, prends des cours de probabilités avec un de nos Sherpas !

Exercices

Maintenant, exerce-toi !

Exercice 1

Soit X une variable aléatoire qui suit une loi binomiale de paramètres n=20 et p=10%

Calcule la probabilité d’avoir 5 succès.
Calcule la probabilité au plus 3 succès.
Calcule la probabilité moins de 3 succès
Calcule la probabilité d’avoir entre 3 et 5 succès (inclus)
Donne l’espérance et la variance

Exercice 2

Tu lances une pièce de monnaie 10 fois de manière indépendante. Chaque fois que tu obtiens face, tu gagnes 1 point.

Quelle est la probabilité d’avoir exactement 3 points ?
Quelle est la probabilité d’avoir 2 points ou moins ?
Quelle est la probabilité d’avoir entre 7 et 9 points (inclus) ?
Quelle est la probabilité de faire carton plein (10 points) ?
Quelle est la probabilité de n’avoir aucun point ?

Corrections

Correction 1

1. $P(X=5)=\binom{20}{5}0,1^5(1-0,1)^{20-5}=\frac{20!}{5!(20-5)!}0,1^5(1-0,1)^{20-5}$

$P(X=5)=\frac{20!}{5!(20-5)!}0,1^5(1-0,1)^{20-5}=0,0319$

Tu as 3,19% d’avoir 5 succès.

💡 Astuce

Il existe la table de la loi binomiale pour trouver directement la probabilité !

Tu as juste à regarder les paramètres n, p et k dans la table et tu as la réponse !

2. $P(X\leq3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)$

$P(X\leq3)=\frac{20!}{0!(20-0)!}\times0,1^0\times(1-0,1)^{20-0}+\frac{20!}{1!(20-1)!}\times0,1^1\times(1-0,1)^{20-1}+\frac{20!}{2!(20-2)!}\times0,1^2\times(1-0,1)^{20-2}+\frac{20!}{3!(20-3)!}\times0,1^3\times(1-0,1)^{20-3}$

$P(X\leq3)=0,1216+0,2702+0,2852+0,1901=0,8671$

Tu as 86,71% d’avoir au plus 3 succès.

3. $P(X<3)=P(X=0)+P(X=1)+P(X=2)=0,1216+0,2702+0,2852=0,6762$

Tu as 67,62% de chance d’avoir moins de 3 succès.

4. $P(3\leq{X}\leq5)=P(X=3)+P(X=4)+P(X=5)$

$P(3\leq{X}\leq5)=0,1901+0,0898+0,0319=0,3118$

Tu as 31,18% de chance d’avoir un succès.

5. On rappelle que $E(X)=np$ et $V(X)=np(1-p)$

$E(X)=20\times0,1=2$

L’espérance est de 2.

$V(X)=20\times0,1\times0,9=1,8$

La variance est de 1,8.

Correction 2

Soit X une variable aléatoire qui suit une loi binomiale de paramètres n=10 et p=0,5 et k le nombre de points que tu gagnes (nombre de succès).

1. $P(X=3)=\frac{10!}{3!(10-3)!}\times0,5^3\times(1-0,5)^{10-3}=0,1172$

Tu as 11,72% de chance d’avoir 3 points (3 fois face).

2. $P(X\leq3)=P(X=0)+P(X=1)+P(X=2)$

$P(X\leq3)=\frac{10!}{0!(10-0)!}\times0,5^0\times(1-0,5)^{20-0}+\frac{10!}{1!(10-1)!}\times0,5^1\times(1-0,5)^{10-1}+\frac{10!}{2!(10-2)!}\times0,5^2\times(1-0,5)^{10-2}$

$P(X\leq3)=0,0010+0,0098+0,0439=0,0547$

Tu as 5,47% de chance d’avoir entre 0 et 2 points (0, 1 ou 2 fois face).

3. $P(7\leq{X}\leq9)=P(X=7)+P(X=8)+P(X=9)$

$P(7\leq{X}\leq9)=\frac{10!}{7!(10-7)!}\times0,5^7\times(1-0,5)^{10-7}+\frac{10!}{8!(10-8)!}\times0,5^8\times(1-0,5)^{10-8}+\frac{10!}{9!(10-9)!}\times0,5^9\times(1-0,5)^{10-9}$

$P(7\leq{X}\leq9)=0,1172+0,0439+0,0098=0,1709$

Tu as 17,09% de chance d’avoir entre 7 et 9 points (7, 8 ou 9 fois face).

4. $P(X=10)=\frac{10!}{10!(10-10)!}\times0,5^10\times(1-0,5)^{10-10}=0,0010$

Tu as 0,1% de chance de n’avoir que des succès (10 fois face).

5. $P(X=0)=\frac{10!}{0!(10-0)!}\times0,5^0\times(1-0,5)^{10-0}=0,0010$

Tu as 0,1% de chance de n’avoir que des échecs (10 fois pile).

💡 Le savais-tu ?

On est dans un jeu où la probabilité d’avoir un succès est égale à celle d’avoir un échec. Donc la probabilité de n’avoir que des succès est égale à celle de n’avoir que des échecs.

On arrive au bout de notre fiche de maths sur la loi binomiale ! On espère qu’elle t’a plu et qu’elle t’a permis de mieux comprendre cette notion primordiale en probabilités. N’hésite pas à prendre des cours de maths avec un de nos Sherpas si tu as des difficultés.