Aujourd’hui, nous allons explorer ensemble un concept mathématique fondamental : la proportionnalité. Ne t’inquiète pas, même si cela peut sembler un peu intimidant au premier abord, on t’explique tout ça de manière claire et simple. 😉
La proportionnalité, qu’est-ce que c’est ? 🤔
La proportionnalité est une relation entre deux quantités qui grandissent ou diminuent ensemble de manière constante. Cela signifie que quand l’une des quantités change, l’autre quantité change également de manière proportionnelle. Par exemple, si on a deux quantités, x et y, et que lorsque x double, y double aussi, alors nous pouvons dire que x et y sont proportionnelles.
Petit exemple 👇
Imagine que tu vendes des pommes à 2 euros l’unité. Si l’on considère le nombre de pommes vendues et le montant total de la vente, ces deux quantités seront proportionnelles. Par exemple, si tu vends 5 pommes, tu gagneras 10 euros. Si tu vends 10 pommes, tu gagneras 20 euros, et ainsi de suite. Tu peux voir que le montant total de la vente est toujours le double du nombre de pommes vendues. C’est ça, la proportionnalité !
À lire aussi
Tu as du mal avec les probas ? Découvre notre article : probabilités : définition, notions, formules 🧮
Rapport de proportionnalité 📏
Le « rapport de proportionnalité » est un concept essentiel en proportionnalité. Il permet d’exprimer la relation entre les valeurs de deux quantités proportionnelles. Il s’agit du rapport constant qui lie ces valeurs !
Prenons un exemple pour mieux comprendre 👇
👉 Supposons que tu as deux quantités, x et y proportionnelles.
👉 Si tu observes que chaque fois que x augmente de 2 unités, y augmente de 3 unités, alors le rapport de proportionnalité entre x et y est de 2/3.
👉 Ce rapport de 2/3 signifie que pour chaque variation de deux unités dans la quantité x, la quantité y varie de trois unités dans la même proportion.
👉 Peu importe les valeurs spécifiques des quantités, tant que le rapport de proportionnalité reste constant, tu peux affirmer que les quantités sont proportionnelles.
L’importance du rapport de proportionnalité réside dans sa constance. Cela signifie que quelle que soit la valeur de x, si tu multiplies ou divises x par un certain nombre, tu dois également multiplier ou diviser y par le même nombre pour maintenir la proportionnalité !
💡 Le savais-tu ?
Le rapport de proportionnalité peut être exprimé sous différentes formes. Parfois, il est donné sous la forme d’une fraction irréductible, comme 2/3 dans notre exemple. Il peut également être exprimé sous forme de nombre décimal, tel que 0,67 (arrondi) dans ce cas.
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
Le produit en croix X
Maintenant que tu as une compréhension solide de la proportionnalité, on te présente une règle très couramment utilisée qui t’aidera à résoudre tes problèmes de proportionnalité de manière plus simple : le produit en croix !
La règle des produits en croix consiste à multiplier les termes en diagonale et à égaler les produits obtenus. Cela ne fonctionne que si les valeurs sont proportionnelles !
Par exemple, si on a l’équation :
On peut appliquer la règle des produits en croix en multipliant 3 par 8 et en divisant 4 pour trouver x, ce qui donne :
En résolvant cette équation, on peut trouver la valeur de x !
Reprenons l’exemple de nos pommes 👇
Tu te rends chez ton petit épicier en face de chez toi qui vends ses pommes par lot de deux à trois euros. Tu souhaites savoir le prix total pour huit pommes. C’est là que notre superbe produit en croix rentre en jeu 🥳
X représente donc le prix de huit pommes
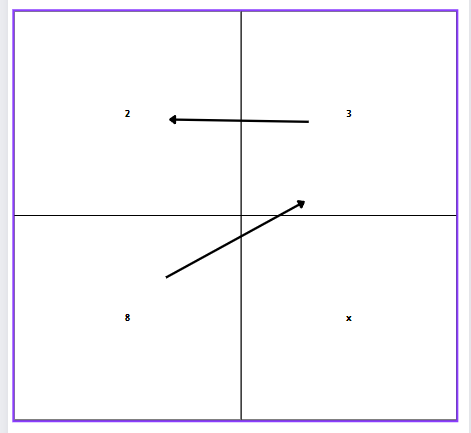
On a ainsi l’équation :
À lire aussi
Représentation graphique 📈
Les graphiques de proportionnalité te seront très utiles pour visualiser et interpréter les relations entre les quantités. Pour créer un graphique de proportionnalité, il suffit de placer les valeurs des quantités proportionnelles sur un système de coordonnées. Les points ainsi obtenus peuvent être reliés par une droite qui passe par l’origine.
Par exemple, reprenons notre exemple précédent avec les pommes vendues 👇
Si on place le nombre de pommes vendues sur l’axe horizontal (abscisse) et le prix total sur l’axe vertical (ordonnée), on obtient une droite qui passe par l’origine. Chaque point sur cette droite représente une paire de valeurs proportionnelles. Plus le nombre de pommes vendues est élevé, plus le montant total de la vente augmente, et vice versa.
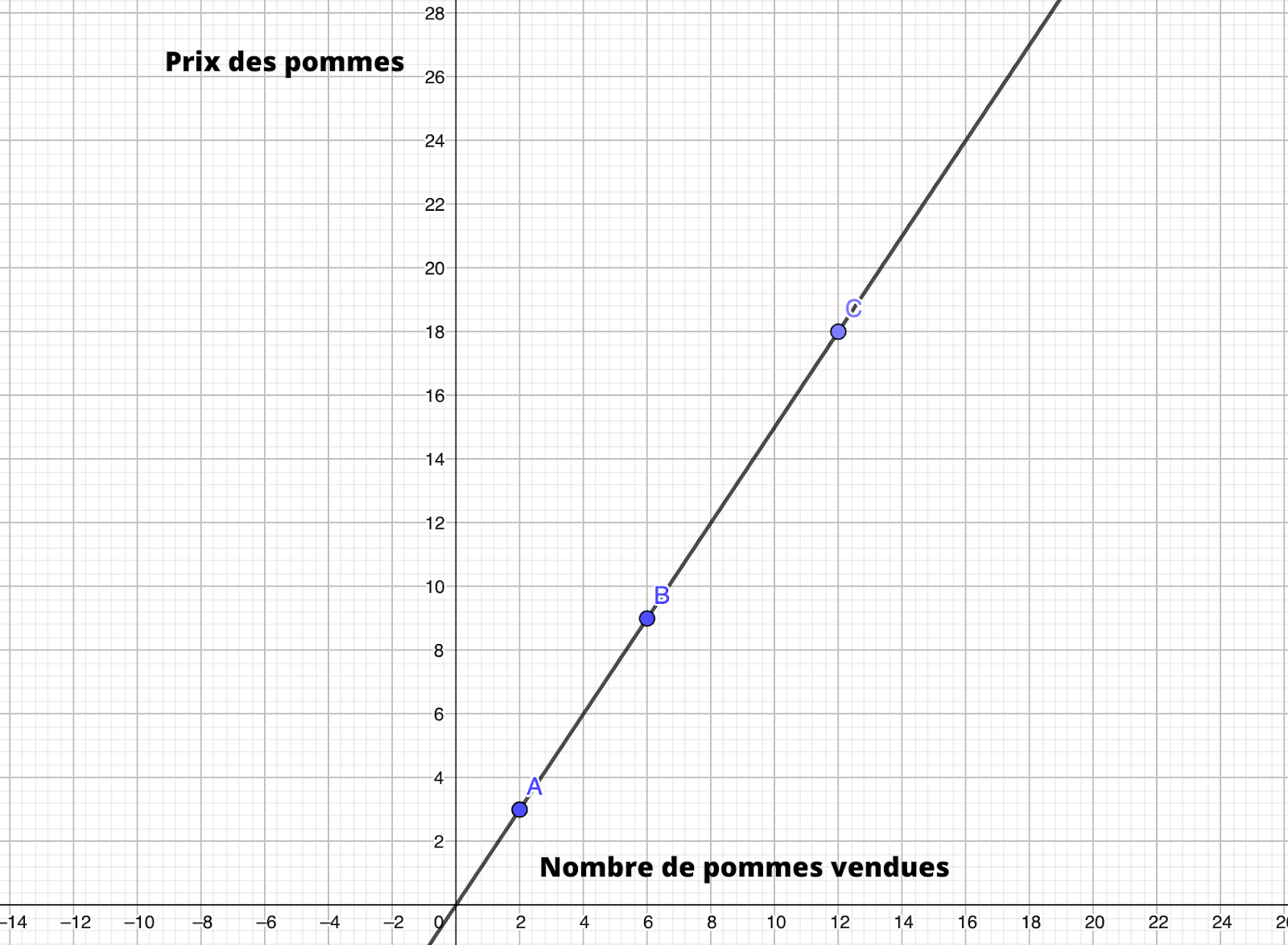
En lisant notre graphique, on peut retrouver notre prix facilement ! Par exemple, le point C nous indique que pour 12 pommes, tu paieras 18 euros !
Ton premier cours particulier de maths est offert ! 🎁
Tous nos profs sont passés par les meilleures écoles de France !
Quand est-elle utilisée ? 🤔
La proportionnalité n’est pas seulement une notion mathématique abstraite, elle est également extrêmement utile dans de nombreux aspects de la vie quotidienne 👇.
🛒 Elle peut être utilisée pour comparer des prix au supermarché en calculant le coût pour une quantité donnée de produit. On ne va pas encore te reparler des pommes, mais tu comprends le principe. 😉
🧑🍳 La proportionnalité est aussi utile en cuisine, notamment lors de l’ajustement des proportions d’une recette. Si tu veux doubler ou diviser par deux une recette, il suffit d’appliquer la proportionnalité pour adapter les quantités d’ingrédients. Par exemple, si une recette demande 250 g de farine pour 4 personnes, tu peux calculer que pour 8 personnes, tu auras besoin de 500 g de farine !
🚶 Les conversions d’unités impliquent souvent la proportionnalité. Par exemple, pour convertir des kilomètres en miles, tu peux utiliser le facteur de conversion (1 km = 0,621371 mile). En multipliant la distance en kilomètres par ce facteur, tu obtiendras la distance équivalente en miles.
Voilà maintenant, tu sais tout sur la proportionnalité ! Retrouve tous nos autres articles de maths juste ici ! Si l’article ne te suffit pas et que tu souhaites te perfectionner, n’hésite pas à prendre des cours particuliers de maths avec l’un de nos Sherpas !



![Comment être fort en maths ? [Méthode]](https://sherpas.com/content/uploads/2021/10/woman-holding-books-3768126.jpg)








