Le programme de maths de troisième est un casse-tête pour de nombreux élèves. Dans cet article, on va te parler du célèbre Théorème de Thalès, troisième chapitre du programme scolaire ! De quoi ça parle, d’où il vient… On te donne les clés pour réussir cette étape et être à l’aise le jour du Brevet ! 🤗
Le théorème de Thalès de long en large
Le théorème de Thalès en 3ème est redouté… On comprend pourquoi ! Après ces quelques explications de cours, tu devrais bien t’en sortir. C’est parti ! 🚀
Qu’est-ce que le théorème de Thalès ? 🧐
Définition
D’un point de vue théorique, le théorème de Thalès est une théorie de géométrie. Elle affirme que dans le plan d’un triangle, une droite parallèle à l’un des côtés du triangle, définit un deuxième triangle avec des angles proportionnels à l’aide des deux autres côtés.

Voici le plan d’un triangle appelé ABC.
La droite DE est une droite parallèle au côté BC. Grâce à cette droite, on obtient un nouveau triangle ADE.
D’après le théorème de Thalès (qu’on t’explique juste après), on définit que les angles du triangle ADE sont proportionnels à ceux du triangle ABC.
D’un point de vue pratique, ce théorème permet de calculer des longueurs et de démontrer qu’en présence de deux droites parallèles, on peut constater des formes proportionnelles.

Collégien en galère ? Ton premier cours est offert ! 🎁
Nos profs sont là pour t’aider à progresser !
D’où vient le théorème de Thalès ? 👀
Il vient directement de Monsieur Thalès en personne, de son vrai nom Thalès de Milet. Philosophe grec et grand savant, Thalès a vécu plus de 500 ans avant J.C. Notamment connu pour son théorème, il est renommé à travers le monde pour bien d’autres exploits : prédiction d’éclipse, chercheur en maths… et surtout en géométrie !
👉 Il est entré dans l’Histoire grâce à ses méthodes d’analyses. Contrairement à ses contemporains, Thalès ne s’appuyait pas sur la mythologie, mais bel et bien sur l’observation et la démonstration.
🔥 Petite anecdote
La première fois que Thalès découvre et met en pratique son théorème, c’était pour déterminer les propriétés de la grande pyramide de Khéops en Égypte !

À lire aussi
✅ Tout comprendre au théorème de Pythagore
Quand utiliser le théorème de Thalès ? ✨
Pour être utilisé, le théorème de Thalès nécessite la présence de deux droites parallèles coupées par deux droites sécantes.
Le reconnaître
Le théorème s’applique seulement pour deux figures.

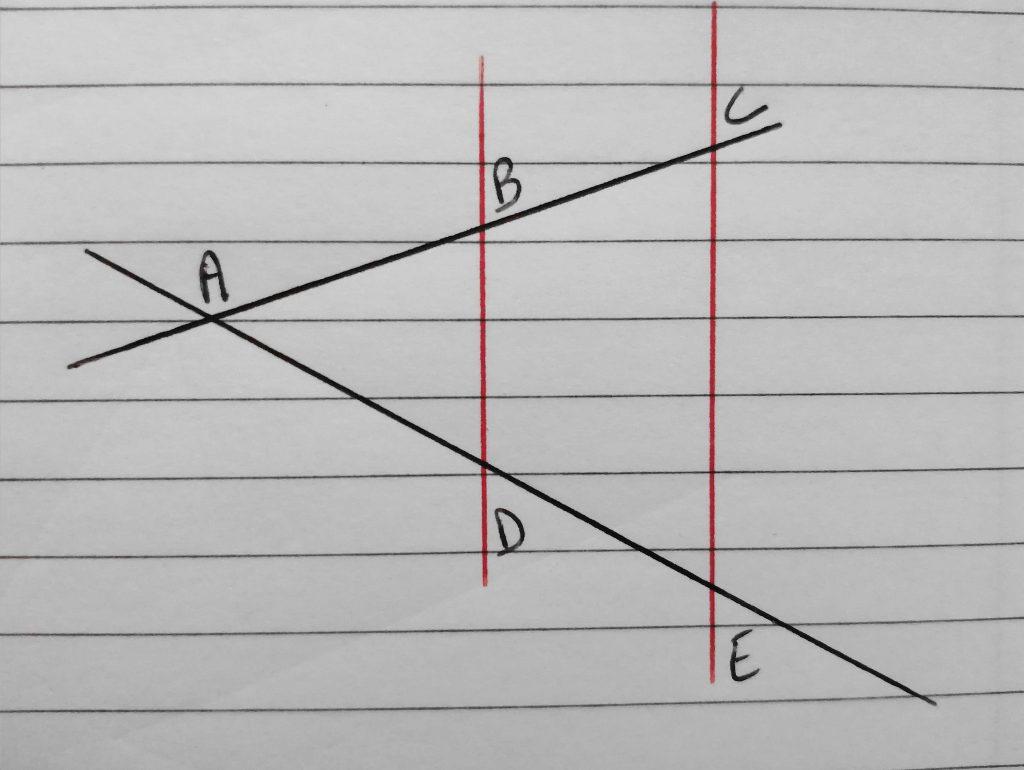
💡 Rappel de cours
- Des droites sont parallèles si elles ne possèdent aucun point en commun. Il s’agit de deux lignes droites allant dans la même direction sans jamais se rencontrer en un point.
- Des droites sont sécantes si elles possèdent un point en commun. Ce point se nomme le point d’intersection.
L’utiliser
Maintenant que tu sais reconnaître les cas de figure où le théorème peut être utilisé, passe à la pratique ! Pour ça, tu as besoin de connaître les valeurs d’au moins trois longueurs.
Voici des exemples pour que tu puisses visualiser.


Le théorème s’applique de la même façon pour les deux configurations de triangle. La seule différence est pour la 1. Les triangles sont distincts, il te faut donc prendre le point de croisement (ici le point N), comme point commun entre les deux figures.
Le théorème de Thalès 📏
Pour chaque figure, on parle de Propriété à appliquer. Voici un petit guide :
- Énonce le théorème et écris les rapports égaux
- Remplace les mesures connues par leur valeur numériques et raie la valeur inutile
- Réalise un produit en croix (des fractions 🥲)
Exemple :
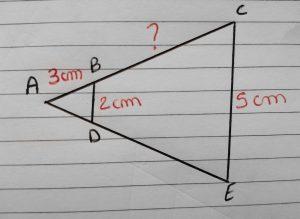
Énoncé : Calcule la longueur de AC et déduis celle du segment BC.
- Dans cette figure, on observe deux triangles. Le triangle ABD et le triangle ACE. Ainsi que la droite [CE] parallèle à la droite [BD].
On sait que [CE] et [BD] sont parallèles, on obtient donc des angles égaux.
Alors les angles ADB et AEC sont égaux ; ABD = ACE et EAC = DAB
- Selon le théorème de Thalès :
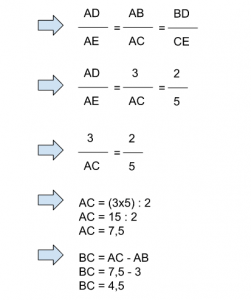
Ainsi AC = 7,5 cm, de ce fait BC = 4,5 cm.
🚨 Pas de secret, l’entraînement sera la clé de ta réussite sur ce chapitre !
👉 Si tu as des difficultés à comprendre la leçon, tu peux te tourner vers un de nos super professeurs de mathématiques. Tu peux le choisir selon ton niveau et tes besoins. Il pourra même t’aider à gérer le brevet, de quoi trouver la perle rare ! 💎
À lire aussi
✅ Le kit pour devenir fort en maths
As-tu compris la méthode ? Essaie cet exercice pour voir ! 🤓
En utilisant le théorème de Thalès, calcule la longueur du segment FJ à 0,1 cm près.
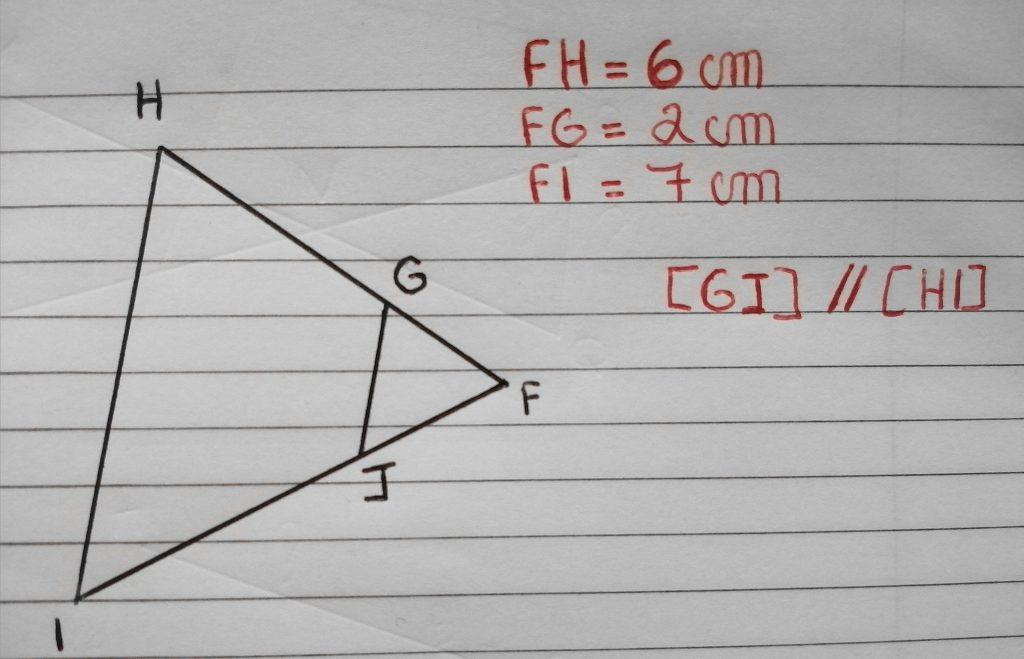
Réponse et démonstration
Dans cette figure, il y a deux triangles : FGJ et FHI. On sait que les droites [GH] et [HI] sont parallèles.
Selon le théorème de Thalès :
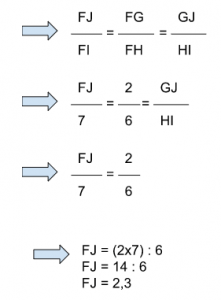
Alors FJ mesure 2,3 cm.
Besoin d’un prof particulier de maths ? ✨
Nos Sherpas sont là pour t’aider à progresser et prendre confiance en toi !
La réciproque du Théorème de Thalès 🤨
Eh oui, ce n’est pas terminé. Comme beaucoup de théorèmes, celui de Thalès possède sa réciproque ! Elle est très utilisée dans le programme de troisième au collège.
La réciproque du théorème de Thalès s’applique lorsque les points considérés sont situés sur deux droites issues d’un même sommet, et que les rapports des longueurs partant de ce sommet sont égaux.

Déterminer deux droites parallèles
En quelques mots, la réciproque du théorème de Thalès permet de démontrer que deux droites sont parallèles (ou non). Auquel cas, tu peux utiliser le théorème.
💡 Petite astuce Sherpa
Pour le calcul de tes équations, tu peux choisir l’ordre que tu souhaites.
👉 On te conseille de prendre la plus petite mesure en haut et la plus grande en bas.
Exemple :
Pour prouver que [WZ] et [YX] sont parallèles, on calcule séparément [VZ/VY] et [VW/VX], et on vérifie qu’ils sont égaux.

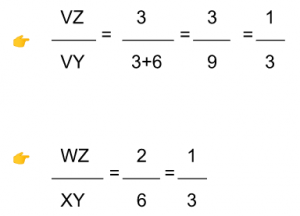
Si [VZ/VY] et [VW/VX] sont égaux, alors d’après la réciproque du théorème de Thalès, les droites [WZ] et [XY] sont parallèles.
Si les rapports ne sont pas égaux, les droites ne sont pas parallèles.
Tu l’auras compris, ce chapitre de mathématique est rempli d’équations et de géométrie. Maintenant que tu sais utiliser le théorème de Thalès et sa réciproque, tu as toutes les cartes en mains pour réussir ce cours de géométrie ! 🃏 Surtout n’oublie pas de bien t’entraîner avec plusieurs exercices. Garde l’œil ouvert sur le blog, on a plein d’articles pour t’aider en mathématiques !
FAQ ✅
Quelle est la formule du théorème de Thalès?
La formule du théorème de Thalès est AB/AC = DE/DF = BE/CF lorsque les droites (DE) et (BC) sont parallèles et (AC) les coupe. Ce théorème établit une proportionnalité entre les segments des droites sécantes.
Comment on utilise le théorème de Thalès?
Le théorème de Thalès est utilisé pour démontrer la proportionnalité des segments lorsque deux droites sont coupées par des droites parallèles. Il est souvent utilisé pour calculer une longueur manquante dans un triangle ou pour prouver que deux droites sont parallèles.
Quand est-ce qu’il faut utiliser le théorème de Thalès?
Il faut utiliser le théorème de Thalès lorsqu’on est confronté à des droites parallèles coupées par des droites sécantes. Ce théorème est particulièrement utile pour déterminer des longueurs inconnues dans un triangle ou pour vérifier la parallélité de deux droites.
Quelle est la réciproque de Thalès?
La réciproque du théorème de Thalès stipule que si, dans un triangle, on a une proportionnalité telle que AB/AC = BE/CF, alors les droites (BE) et (CF) sont parallèles. Elle permet de déduire la parallélité basée sur la proportionnalité des segments.
Comment savoir si un triangle est rectangle avec Thalès?
Avec Thalès, si dans un triangle, deux segments sont proportionnels aux deux plus grands côtés et sont issus du même sommet, alors ce triangle est rectangle. La réciproque du théorème de Thalès est souvent utilisée pour démontrer cela.














