Les triangles et vous, c’est une histoire (un peu 🥲) compliquée, surtout quand il s’agit de s’y retrouver avec tous ces angles et ces côtés ? Pas de panique ! Les Sherpas vous ont préparé une série d’articles « rappel » pour vous donner un coup de pouce.
Aujourd’hui, on vous propose une fiche de cours sur les triangles en géométrie. Triangle isocèle, triangle rectangle, triangle quelconque… (Re)découvrez-les tous ! 🚀
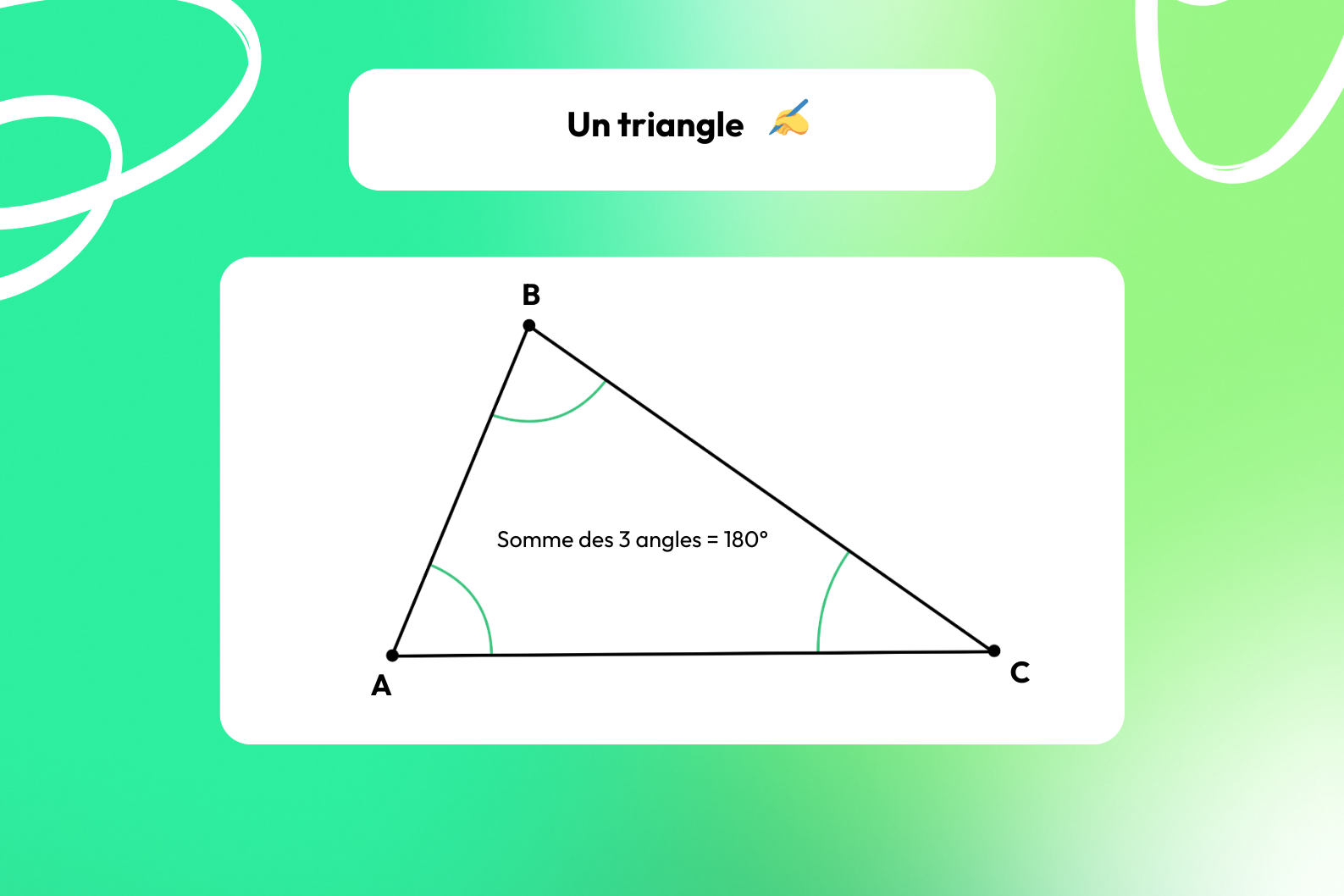
Un triangle, c’est quoi en géométrie ? 🤔
Un triangle est un polygone ✅
Commençons par le commencement, c’est-à-dire les définitions ! En géométrie euclidienne, un triangle est un polygone qui possède 3 côtés, 3 sommets et 3 angles.
📍 La somme de ses angles vaut 180°.
💡 Le saviez-vous ?
Le mot « triangle » vient du latin triangulus, qui est lui-même un dérivé de angulus (angle), auquel s’ajoute le préfixe tri- (trois). Plutôt logique, n’est-ce pas ? 😌
Pour rappel, un polygone est une figure plane fermée par des segments de droites. Il est dit « régulier » lorsque ses angles sont égaux les uns aux autres.
↪️ Exemples de polygones : le pentagone et l’hexagone.
Un triangle possède des droites particulières ✅
En mathématiques, on distingue 4 types de droites particulières dans un triangle : les médianes, les bissectrices, les hauteurs et les médiatrices. Chaque triangle possède 3 de ces droites. On vous en dit plus dans cette sous-partie ! 👇

Les médianes 📌
👉 Ces droites relient un sommet du triangle au milieu du côté opposé.
👉 Les médianes se rejoignent en un point unique appelé « centre de gravité du triangle ».
Ce point divise chaque médiane en deux segments, l’un étant deux fois plus long que l’autre, avec le centre de gravité situé aux deux tiers de la médiane à partir du sommet.
À lire aussi
🔢 Guide : comment réconcilier son enfant avec les maths !
Les hauteurs 📌
👉 Les hauteurs sont des droites perpendiculaires à un côté du triangle.
👉 Elles passent par le sommet opposé.
👉 Elles se rencontrent en un point appelé « orthocentre du triangle ».
Selon le type de triangle, l’orthocentre peut se situer à l’intérieur ou à l’extérieur.
À lire aussi
Les médiatrices 📌
👉 Ces droites sont perpendiculaires à un côté du triangle et passent par son milieu.
👉 Elles se coupent en un point appelé « centre du cercle circonscrit du triangle ».
Ce point est équidistant des trois sommets du triangle.
À lire aussi
📖 La véritable histoire des tables de multiplication
Les bissectrices 📌
👉 Ces droites divisent un angle du triangle en deux angles égaux.
👉 Les bissectrices se rejoignent en un point appelé « centre du cercle inscrit du triangle ».
Ce point est équidistant des trois côtés du triangle.
Besoin d’un prof particulier exceptionnel ? ✨
Nos Sherpas sont là pour aider votre enfant à progresser et à prendre confiance en lui.
Les propriétés des principaux triangles 🔎
Maintenant, passons aux choses sérieuses : les propriétés des triangles ! Vous verrez, ce n’est pas aussi dur qu’il n’y paraît. En plus, on vous a préparé des schémas. 😉
Le triangle quelconque 🔼
📍 Voici ce que vous devez savoir sur le triangle quelconque :
- Il possède 3 côtés différents ;
- Il a 3 angles inégaux ;
- La somme des angles est égale à 180°.
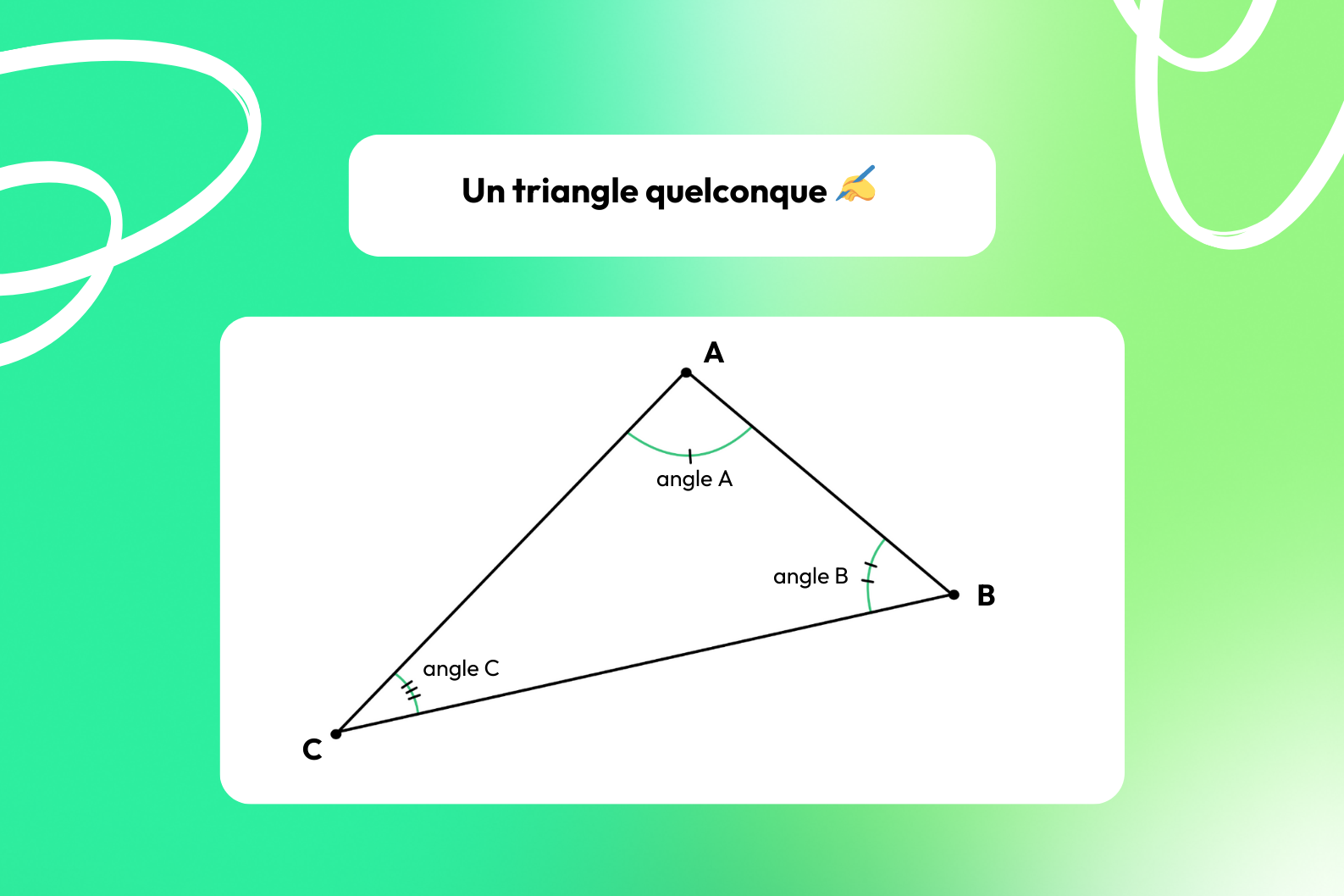
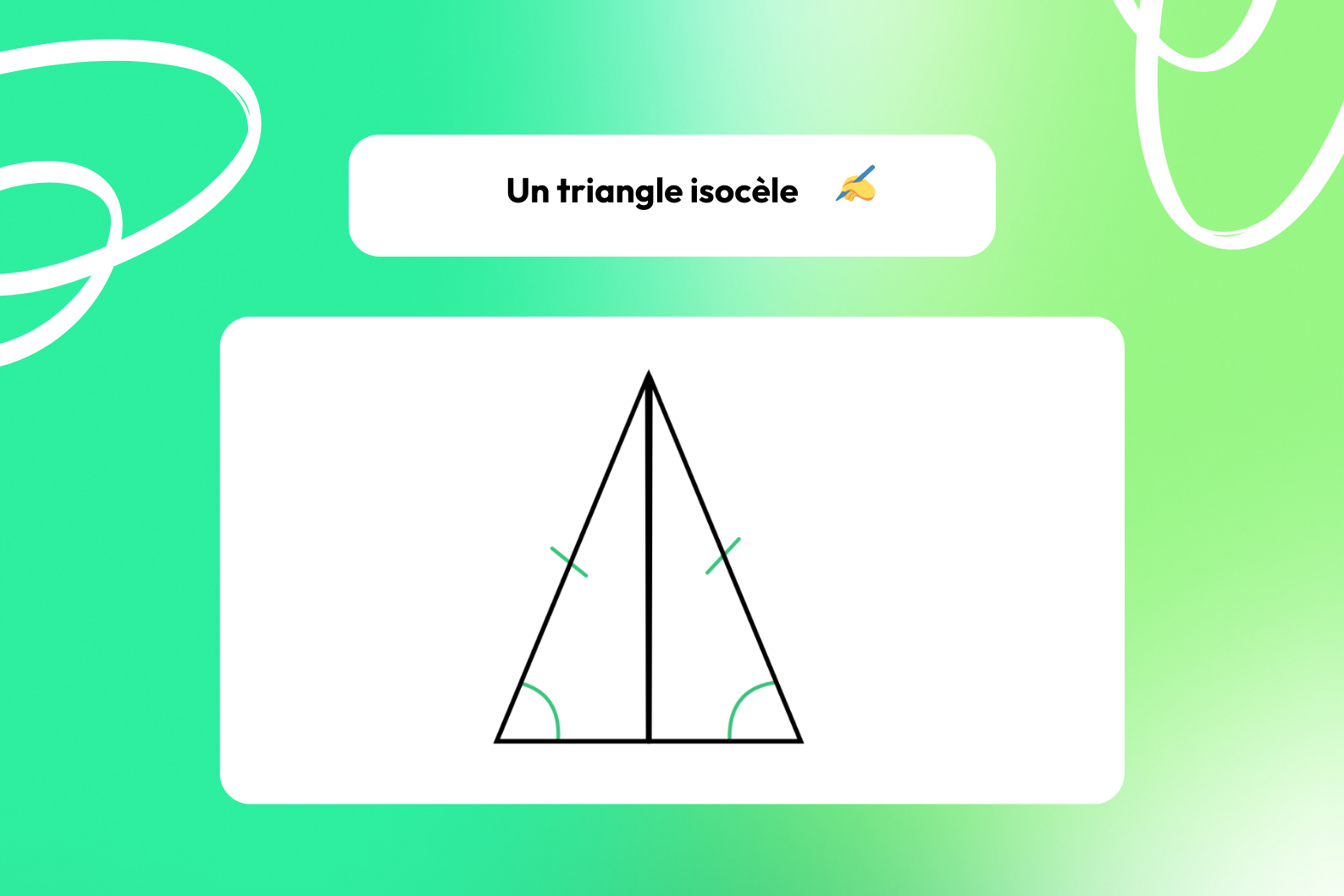
Le triangle isocèle 🔼
📍 Voici ce que vous devez savoir sur le triangle isocèle :
- Il a 2 côtés de même longueur,
- Les angles à la base (les angles opposés aux côtés égaux) sont égaux,
- Le sommet opposé à la base est symétrique par rapport à la médiatrice de la base.
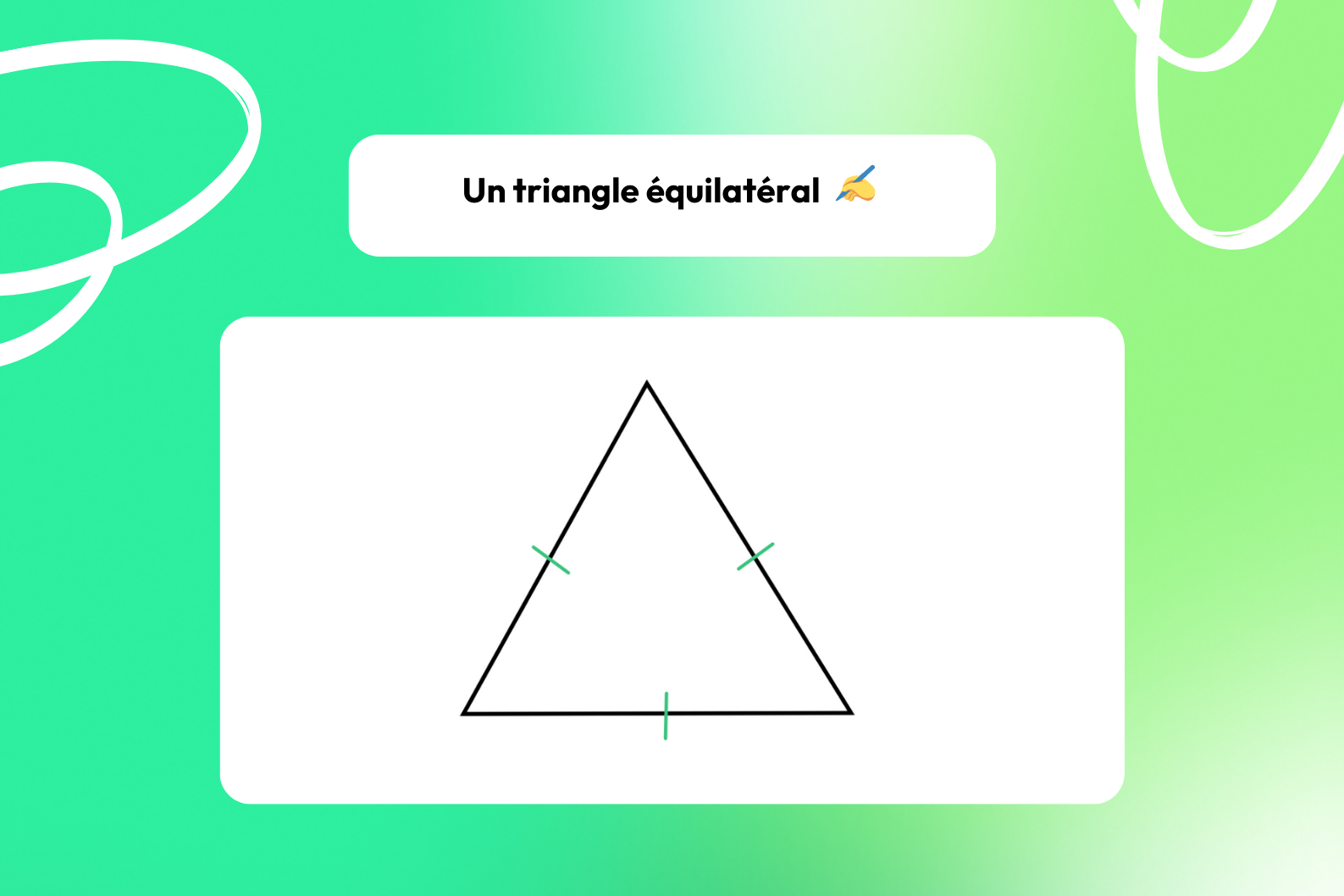
Le triangle équilatéral 🔼
📍 Voici ce que vous devez savoir sur le triangle équilatéral :
- Il possède 3 côtés de même longueur ;
- Tous les angles intérieurs sont égaux et mesurent 60° ;
- Il possède une symétrie axiale selon n’importe quelle médiane.
Le triangle rectangle 🔼
📍 Voici ce que vous devez savoir sur le triangle rectangle :
- Il possède 1 angle droit (90°) ;
- Le côté opposé à l’angle droit est l’hypoténuse (c’est le plus long côté du triangle).
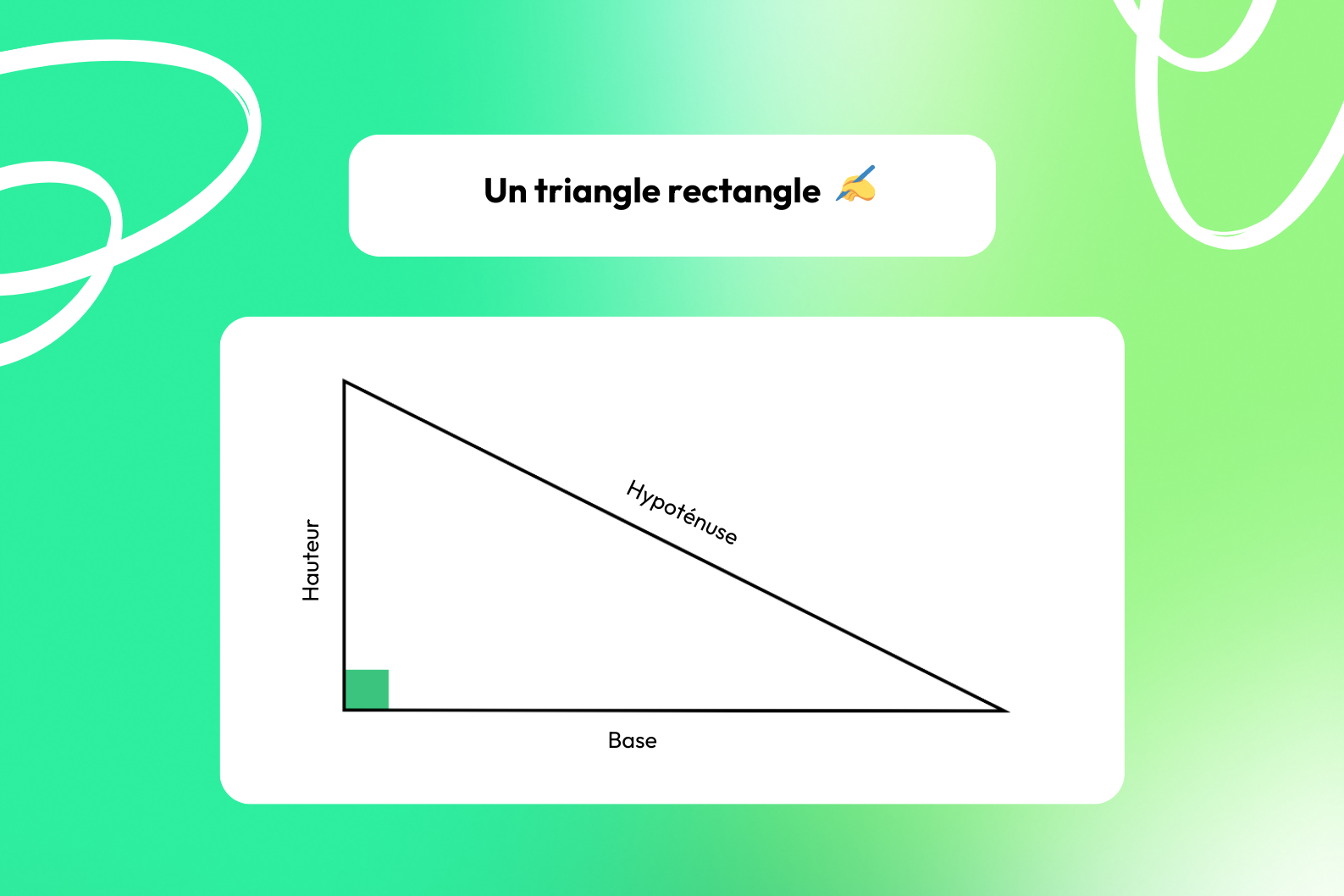
Selon le théorème de Pythagore, la somme des carrés des longueurs des deux autres côtés est égale au carré de la longueur de l’hypoténuse. La hauteur relative à l’hypoténuse divise le triangle en deux triangles rectangles similaires au triangle initial.
👉 Le centre du cercle circonscrit est situé au milieu de l’hypoténuse.
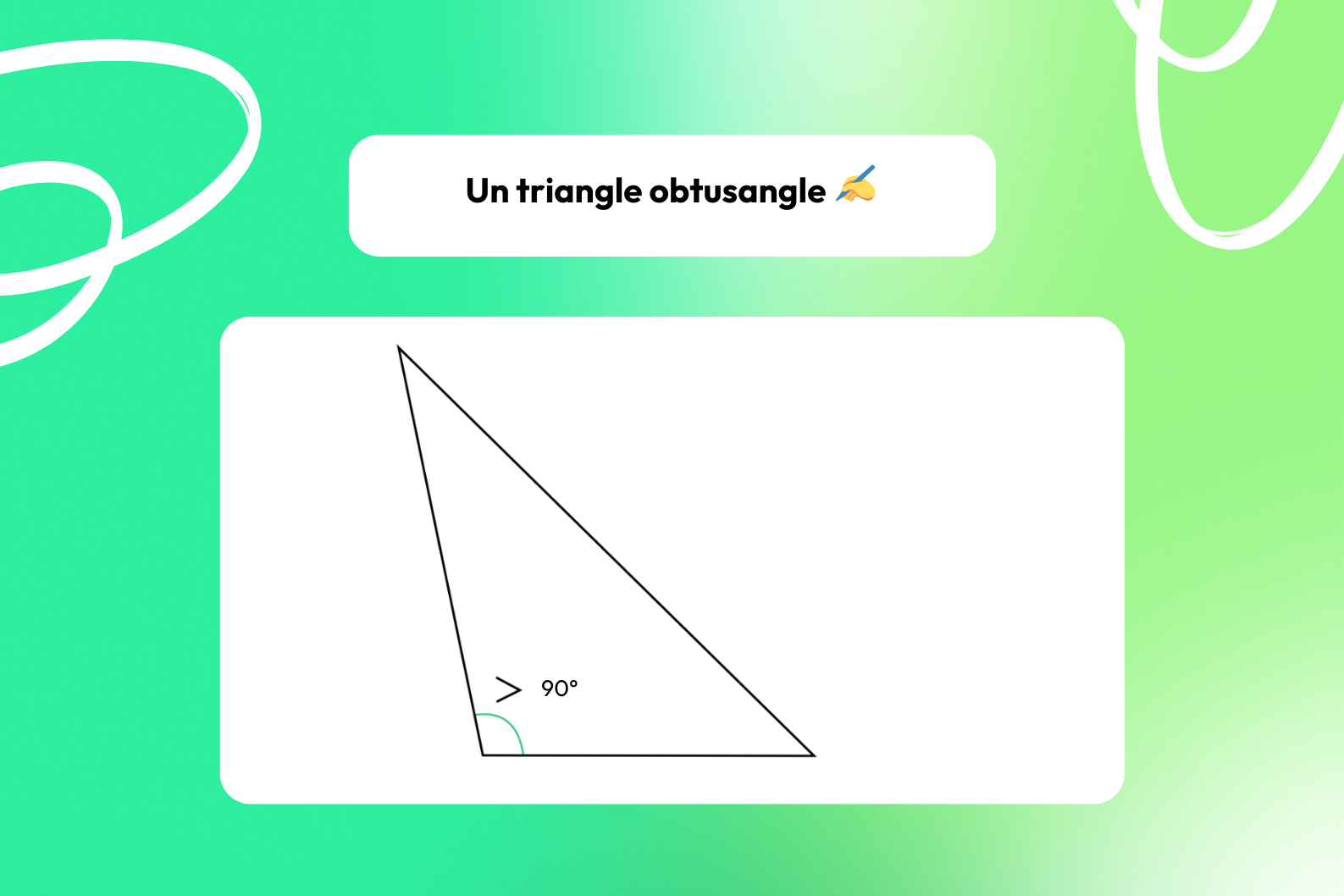
Le triangle obtusangle 🔼
📍 Voici ce que vous devez savoir sur le triangle obtusangle :
- Il a 1 angle intérieur supérieur à 90° ;
- L’angle obtus est toujours opposé au plus long côté ;
- L’orthocentre se trouve à l’extérieur du triangle.
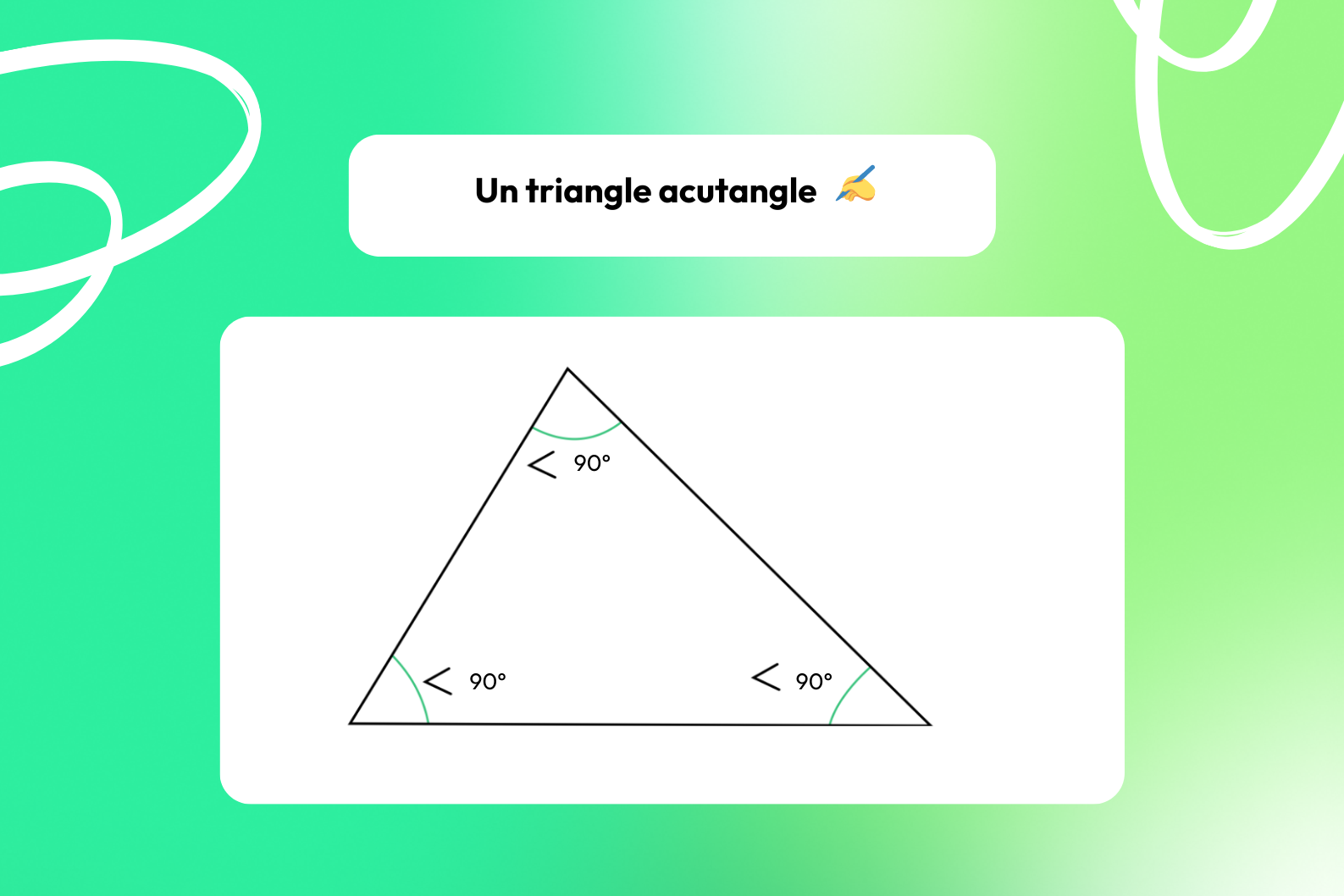
Le triangle acutangle 🔼
📍 Voici ce que vous devez savoir sur le triangle acutangle :
- Il a 3 angles intérieurs inférieurs à 90° ;
- Tous les angles sont aigus ;
- L’orthocentre se situe à l’intérieur du triangle.
Le premier cours particulier est offert ! 🎁
Aidez votre enfant en lui offrant des cours avec un étudiant passé par une des meilleures écoles de France.
Comment calculer l’aire de ces triangles ? 🧐
Pour rappel, l’aire représente une surface géométrique. Cette mesure indique sa taille en unités carrées (en cm² le plus souvent). Chaque figure possède une formule spécifique pour calculer son aire. Dans le cas des triangles, la formule générale est :
Aire = (Base x Hauteur) : 2
🧑🏫 Note : pour connaître l’aire d’un triangle, il vous faut connaître la mesure de la base (soit, l’un des côtés du triangle) ET la mesure de la hauteur.
L’aire des triangles quelconques, isocèles et équilatéraux 🧮
Pour ces triangles, la formule de l’aire reste la même. La base (B) est un côté du triangle et la hauteur (h) est la distance perpendiculaire entre cette base et le sommet opposé.
↪️ Exemple
Pour connaître l’aire d’un triangle ayant une base de 7 cm et une hauteur de 4 cm, on applique la formule ci-dessous. Ça nous donne une aire de 14 cm².
Aire = (7 cm x 4 cm) : 2
Aire = 28 cm² : 2
Aire = 14 cm²
L’aire des triangles rectangles 🧮
Les triangles rectangles sont des cas particuliers où un angle est droit (90°). Un triangle rectangle peut être considéré comme la moitié d’un rectangle.
Par conséquent, l’aire d’un triangle rectangle peut être calculée en utilisant la même formule que pour un rectangle, puis en divisant par deux. 🧑🤝🧑
↪️ Exemple
Imaginons que vous avez un triangle rectangle avec les côtés perpendiculaires AC = 4 cm et BC = 8 cm. Ce triangle est droit en C. Pour calculer son aire, il faut appliquer la formule ci-dessous, ce qui nous donne une aire de 16 cm².
Aire = (8 cm x 4 cm) : 2
Aire = 32 cm² : 2
Aire = 16 cm²
Conclusion
Cet article est maintenant terminé. On espère qu’il vous a permis de faire remonter à la surface de vieux souvenirs de mathématiques. Et n’oubliez pas que, si votre enfant a besoin d’aide, vous pouvez lui offrir des cours de soutien scolaire de mathématiques. À bientôt !