Notion essentielle de la fin de primaire et du collège, surtout en 4ᵉ, la proportionnalité est un des piliers des mathématiques lors de la scolarité de votre enfant. 💪
C’est pourquoi, en tant que parent, vous devez en savoir un minimum sur le sujet. En bons samaritains, on a décidé de vous faire un cours pour vous rappeler le bon vieux temps et vous replonger dans votre livre de mathématiques de quand vous aviez à peine 15 ans. 📖

Ne prenez pas peur face aux seringues, il s’agit seulement d’une piqûre de rappel. Vous êtes concentré ? C’est parti ! 💉
La notion de proportionnalité 🤔
Commençons par quelques éléments de définition, histoire de vous rafraîchir doucement la mémoire.
Explication & définition ✍️
✒️ Définition
Deux valeurs sont proportionnelles si lorsqu’on en multiplie une par un nombre, l’autre valeur est également multipliée par ce même nombre.
En bref, les deux grandeurs sont dites « proportionnelles » si lorsqu’une grandeur augmente, l’autre augmente aussi dans la même proportion. Ce qui signifie qu’elles ont, en effet, le même multiplicateur.
Vous n’avez toujours pas compris ? On va prendre pour exemple les deux valeurs suivantes : 1 et 3,5. La valeur « 1 » devient « 2 » et la valeur « 3,5 » devient « 7 ». Les grandeurs 1 et 3,5 sont-elles proportionnelles ? 🧐
La réponse est oui, car elles ont toutes les deux étaient multipliées par 2.
1 x 2 = 2.
3,5 x 2 = 7.
Autre exemple :
On a un 2 qui augmente et devient « 4 » et à côté, le chiffre décimal 1,2 qui devient 2,5. Les valeurs « 2 » et « 1,2 » sont-elles proportionnelles ? Non, car leur multiplicateur n’est pas le même. ❌
En effet, 2 a été multiplié par 2 pour obtenir 4, mais 1,2 x 2 n’est pas égal à 2,5 mais bien à 2,4. Les deux grandeurs n’ont donc pas augmenté dans la même proportion.
Les représentations graphiques 📈
Avant de passer au graphique, prenons un tableau pour mieux nous aider à comprendre cette notion de proportionnalité.
| Grandeur 1 | 1 | 2 | 6 |
| Grandeur 2 | 1,5 | 3 | 9 |
Notre question est la suivante : s’agit-il d’un tableau de proportionnalité ? Eh bien oui, car toutes les valeurs du haut sont multipliées par « 1,5 » pour obtenir les grandeurs du bas.
1 x 1,5 = 1,5.
2 x 1,5 = 3.
6 x 1,5 =9.
1,5 est donc appelé « le coefficient de proportionnalité ». Dans un tableau, vous pouvez reconnaître une situation de proportionnalité lorsqu’il existe un coefficient de proportionnalité. 👍
Représentons tous ces nombres sur un graphique (repère), que voici :
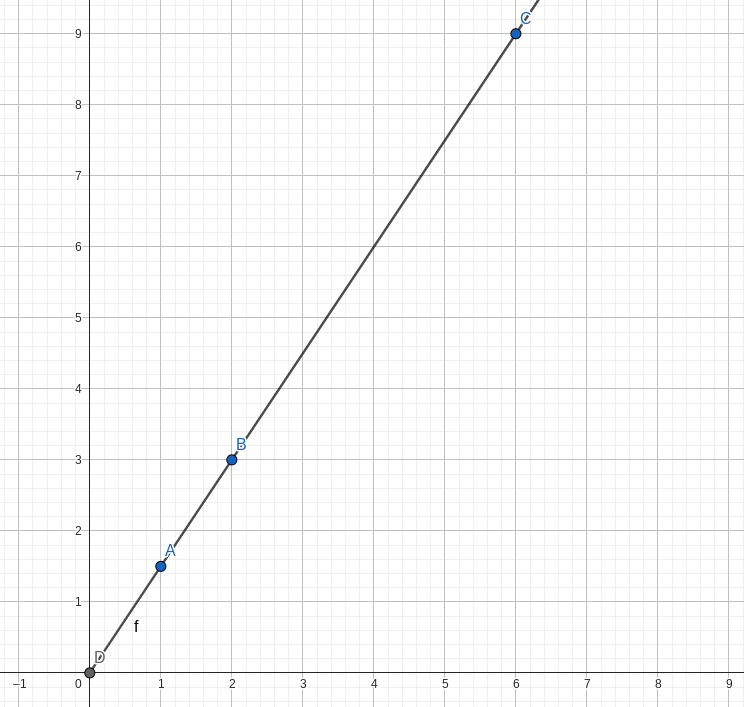
On a placé 1; 2 et 6 sur l’axe des abscisses et les valeurs correspondantes (1,5; 3 et 9) sur l’axe des ordonnées.
Sur un graphique, on parle de situation de proportionnalité lorsque cette dernière est représentée avec des points qui sont alignés avec l’origine. 📏
Besoin d’un prof particulier exceptionnel ? ✨
Nos Sherpas sont là pour aider votre enfant à progresser et à prendre confiance en lui.
Produit en croix ❎
On considère le tableau suivant :

Explication et exemple 🔎
Dans un tableau de proportionnalité, on a l’égalité suivante : a x d = b x c. On a donc une égalité en croix entre les diagonales b/c et a/d, d’où le nom de « produit (le résultat d’une multiplication) en croix ».
C’est bien beau toutes ces lettres, mais prenons un exemple avec des chiffres et des nombres pour mieux comprendre tout cela :
| Grandeur 1 | 4 | 5 |
| Grandeur 2 | 6,8 | 8,5 |
Les grandeurs 1 et 2 sont-elles proportionnelles ? 👀
Si 6,8 x 5 = 4 x 8,5, alors ce sera le cas.
Et en effet, 6,8 x 5 = 34 et 4 x 8,5 = 34 aussi ! D’après la propriété des produits en croix, on peut en déduire que les deux valeurs (grandeurs) sont proportionnelles.
La quatrième proportionnelle 👁️
Le terme de « quatrième proportionnelle » est utilisé pour décrire une situation de proportionnalité dans laquelle on ne connaît que trois nombres sur les quatre et où il faut donc trouver ce quatrième nombre encore inconnu.
Pour comprendre, faisons un petit exercice :
3,5 kg de fraises coûtent 8 €. Quel est le prix de 2 kg ? 🍓
Commençons par remplir notre joli tableau avec les valeurs que l’on a déjà.
| Prix (€) | 8 | 𝑥 |
| Masse (kg) | 3,5 | 2 |
Ce « 𝑥 », c’est justement ce qu’on appelle « la quatrième de proportionnalité » et on doit trouver ce qui se cache derrière.
𝑥 = 2 x 8 ÷ 3,5
= 16 ÷ 3,5
= 4,57.
Le prix de 2 kg de fraises est donc de 4,57 €.
Les fruits, c’est bien pour progresser en maths, des cours de soutien scolaire avec l’un de nos Sherpas, c’est mieux ! 🔥
Applications dans la vie quotidienne 🎒
La proportionnalité ce n’est pas seulement une notion théorique qui ne servirait qu’en classe de maths et pas ailleurs. On utilise les proportions dans la vie courante, on va vous le prouver !
La cuisine 🧑🍳
La proportionnalité est présente partout dans notre quotidien et notamment en cuisine. Allez aux fourneaux ! 🍲
Dans votre recette pour faire votre plus beau risotto, vous devez mettre 125 g de champignons pour 2 personnes, mais vous ne savez pas quelle quantité mettre si vous avez 5 couverts et non plus 2. 🍄
C’est là que la quatrième de proportionnelle intervient :
| Nb de personnes (unité) | 2 | 5 |
| Masse (g) | 125 | 𝑥 |
𝑥 = 125 x 5 ÷ 2
= 625 ÷ 2
= 312,5.
Pour votre recette pour 5 personnes, prenez donc 312,5 g (c’est très précis) de champignons !
La vitesse (moyenne) 🚘
Lors d’un trajet uniforme (en voiture, par exemple), la durée du voyage et la distance parcourue sont proportionnelles. C’est la vitesse qui est le coefficient de proportionnalité. ⚡
Par exemple, si vous allez à 110 km/h de moyenne et vous souhaitez calculer des distances en kilomètres et/ ou des durées en heure :
👣 vous multipliez les durées en heures par 110 pour avoir les distances parcourues en km,
🕰️ ou vous divisez les distances en km par 110 pour obtenir les durées en heures.
💡 Comment connaître la vitesse moyenne ?
Lors d’un trajet d’une distance « d » en un temps « t », la vitesse moyenne, que l’on va appeler « v », est égale à : v = d ÷ t.
Exemple :
Vous parcourez 3,4 km en 15 min à pied (belle foulée). Pour connaître votre vitesse moyenne en km/h, divisez la distance par la durée de votre parcours.
Sachant que 15 minutes = 0,25 heure, on obtient :
v = 3,4 ÷ 0,25 = 13,6 km/h.

Retour du produit en croix 🔙
C’est le retour du calcul en croix et de la quatrième proportionnelle. Sur le sujet de la vitesse, cela va nous servir aussi.
Imaginez que vous souhaitiez calculer une distance et que vous connaissez déjà la vitesse et la durée du chemin ou que vous voulez connaître la durée et que vous avez la vitesse et la distance parcourue. Pour cela, on utilise le fameux produit en croix. 🧠
Exercice :
Un cycliste se déplace à 48 km/h de moyenne (et fait donc logiquement 48 km en 1 heure), combien lui faudrait-il de temps pour parcourir 123 km ? 🚴
Réponse
Vous avez donc le tableau suivant, grâce aux informations que vous avez dans l’énoncé :
| Distance parcourue (km) | 48 | 123 |
| Durée (h) | 1 | 𝑥 |
𝑥 = 1 x 123 ÷ 48
= 2,5625 (soit environ 2h 34 min)
La proportionnalité est présente dans plein de situations du quotidien, on aurait aussi pu vous parler de pourcentages de réduction ou d’échelles sur une carte géographique, etc. 🗺️
On pense toutefois avoir fait le tour de cette notion essentielle dans le programme de maths du collège. 📚
Le premier cours particulier est offert ! 🎁
Aidez votre enfant en lui offrant des cours avec un étudiant passé par une des meilleures écoles de France.
Récap ✅
1️⃣ Deux grandeurs sont dites « proportionnelles » si lorsqu’une grandeur augmente, l’autre augmente aussi dans la même proportion. Ce qui signifie qu’elles ont, en effet, le même multiplicateur.
2️⃣ Dans un tableau avec deux grandeurs, vous pouvez reconnaître une situation de proportionnalité lorsqu’il existe un coefficient de proportionnalité.
3️⃣ Sur un graphique (un repère), on parle de situation de proportionnalité lorsque cette dernière est représentée avec des points qui sont ALIGNÉS avec l’origine.
4️⃣ Dans les tableaux de proportionnalité, on a l’égalité (en croix) suivante : a x d = b x c.

5️⃣ La « quatrième proportionnelle » désigne une situation de proportionnalité dans laquelle on ne connaît que trois nombres sur les quatre et où il faut donc trouver cette quatrième (proportionnelle) valeur encore inconnue.
Vous ne serez désormais plus à la ramasse sur le programme du collège en mathématiques et, plus particulièrement, sur la notion de proportionnalité. 💥
Et si votre aide ne suffit pas, votre enfant peut réussir grâce à nos cours de soutien scolaire de maths en ligne avec l’un de nos professeurs ! 🙂









